Dreieck Rechner
Online Rechner für alle Dreiecksberechnungen - Seiten, Winkel, Fläche, Umfang
|
|
Geben Sie mindestens drei bekannte Werte ein (Seiten und/oder Winkel). Der Rechner berechnet automatisch alle anderen Eigenschaften des Dreiecks.
Eingaberegeln
• Mindestens eine Seite muss gegeben sein
• Winkel in Grad eingeben
• Dezimalzahlen mit Punkt oder Komma
• Gültige Kombinationen: SSS, SWS, WSW, SSW
Das Dreieck - Grundlagen der Geometrie
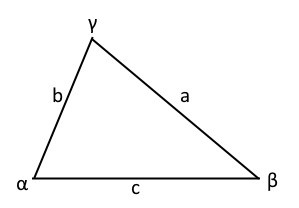
Ein Dreieck ist ein Polygon mit drei Ecken und drei Seiten. Es ist die einfachste geschlossene Figur in der ebenen Geometrie und bildet die Grundlage für viele geometrische Berechnungen. Jedes Dreieck hat drei Seiten ($a$, $b$, $c$) und drei Innenwinkel ($\alpha$, $\beta$, $\gamma$).
Grundbegriffe:
- Seiten: $a$, $b$, $c$ (die Längen der drei Seiten)
- Winkel: $\alpha$ (gegenüber Seite $a$), $\beta$ (gegenüber Seite $b$), $\gamma$ (gegenüber Seite $c$)
- Fläche ($A$): Der Flächeninhalt des Dreiecks
- Umfang ($U$): Die Summe aller drei Seitenlängen
Wichtige Formeln für Dreiecke
Winkelsumme:
$$\alpha + \beta + \gamma = 180°$$
Umfang:
$$U = a + b + c$$
Fläche (Heron'sche Formel):
$$A = \sqrt{s(s-a)(s-b)(s-c)}$$
wobei $s = \frac{a+b+c}{2}$ der Halbumfang ist.
Sinussatz:
$$\frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma}$$
Cosinussatz:
$$c^2 = a^2 + b^2 - 2ab \cos \gamma$$
Beispielrechnung
Gegeben: Seiten $a = 5$ cm, $b = 7$ cm, $c = 9$ cm
Umfang berechnen:
$U = a + b + c = 5 + 7 + 9 = 21$ cm
Fläche berechnen (Heron):
$s = \frac{5 + 7 + 9}{2} = 10{,}5$
$A = \sqrt{10{,}5 \times (10{,}5-5) \times (10{,}5-7) \times (10{,}5-9)}$
$A = \sqrt{10{,}5 \times 5{,}5 \times 3{,}5 \times 1{,}5} \approx 17{,}41$ cm²
Winkel $\alpha$ berechnen (Cosinussatz):
$\cos \alpha = \frac{b^2 + c^2 - a^2}{2bc}$
$\cos \alpha = \frac{49 + 81 - 25}{2 \times 7 \times 9} = \frac{105}{126} \approx 0{,}833$
$\alpha = \arccos(0{,}833) \approx 33{,}56°$
Dreiecksarten
Nach Seiten:
- Gleichseitiges Dreieck: Alle drei Seiten gleich lang ($a = b = c$)
- Gleichschenkliges Dreieck: Zwei Seiten gleich lang
- Unregelmäßiges Dreieck: Alle Seiten unterschiedlich lang
- Rechtwinkliges Dreieck: Ein Winkel = 90°
- Spitzwinkliges Dreieck: Alle Winkel < 90°
- Stumpfwinkliges Dreieck: Ein Winkel > 90°
Eingabemöglichkeiten
Der Rechner akzeptiert verschiedene Kombinationen von bekannten Werten:
- SSS: Alle drei Seiten bekannt
- SWS: Zwei Seiten und der eingeschlossene Winkel
- WSW: Ein Seite und die beiden anliegenden Winkel
- SSW: Zwei Seiten und ein Winkel (Achtung: kann mehrdeutig sein)
Wichtig: Mindestens eine Seite muss immer bekannt sein, da sich aus reinen Winkelangaben keine absolute Größe bestimmen lässt.
KreisDreiecke
DreieckSpezielle Vierecke
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)
QuadratPolygone
Rechteck
Parallelogramm
Raute
Trapez
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rechteckiger Rahmen
Konkaves Viereck Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt
Pentagon (Fünfeck)Allgemeine Vierecke
Hexagon (Sechseck)
Heptagon (Siebeneck)
Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)