Dreieck Seitenhalbierende Rechner

Online Rechner für Seitenhalbierenden (Medianen), Schwerpunkt und Schwerlinien

Dreieck Seitenhalbierende Rechner

Medianen, Schwerpunkt und Schwerlinien berechnen

Geben Sie mindestens 3 Werte ein - Seitenhalbierenden werden berechnet:

Seitenhalbierenden: Verbinden Eckpunkte mit gegenüberliegenden Seitenmittelpunkten

Seite a

Einheiten

Seite b

Einheiten

Seite c

Einheiten

Median m_a

Einheiten

Median m_b

Einheiten

Median m_c

Einheiten

Dezimalstellen

Mindestens 3 Werte - Medianen & Schwerpunkt

Schnell-Beispiele:

⭕

Seitenhalbierenden: Schwerpunkt teilt jede Median im Verhältnis 2:1

Dreiecksseiten:

Seite a

Seite b

Seite c

Seitenhalbierenden (Medianen):

Median m_a

Von A zur Seite a

Median m_b

Von B zur Seite b

Median m_c

Von C zur Seite c

Dreiecks-Eigenschaften:

Fläche A

Umfang U

Geben Sie die drei Seitenlängen ein oder kombinieren Sie Seiten mit Medianen. Der Rechner berechnet automatisch alle Seitenhalbierenden und Dreieckseigenschaften.

Eingaberegeln

• Mindestens drei Werte erforderlich
• Entweder alle drei Seiten oder Kombination
• Dezimalzahlen mit Punkt oder Komma
• Dreiecksungleichung muss erfüllt sein

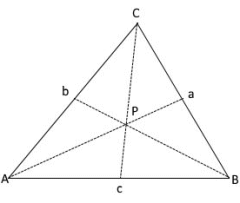
Median-Eigenschaften

• Schwerpunkt: Alle Medianen treffen sich in einem Punkt
• Teilung 2:1: Schwerpunkt teilt jede Median im Verhältnis 2:1
• Flächenteilung: Jede Median teilt das Dreieck in zwei gleiche Hälften

Seitenhalbierenden (Medianen) im Dreieck

Eine Seitenhalbierende (auch Median oder Schwerlinie genannt) ist eine Strecke, die einen Eckpunkt des Dreiecks mit dem Mittelpunkt der gegenüberliegenden Seite verbindet. Jedes Dreieck hat drei Seitenhalbierenden, die sich alle im Schwerpunkt treffen.

Eigenschaften der Seitenhalbierenden:

Schwerpunkt: Alle drei Medianen schneiden sich in einem Punkt
Teilungsverhältnis: Der Schwerpunkt teilt jede Median im Verhältnis 2:1
Flächenteilung: Jede Median teilt das Dreieck in zwei flächengleiche Hälften
Parallelogramm der Medianen: Die Medianen bilden ein charakteristisches Muster

Formeln für Seitenhalbierenden

Seitenhalbierenden Formeln:

Bezeichnungen: $a$, $b$, $c$ = Seiten, $m_a$, $m_b$, $m_c$ = Medianen (Seitenhalbierenden)

Medianformeln:
$$m_a = \frac{1}{2}\sqrt{2b^2 + 2c^2 - a^2}$$ $$m_b = \frac{1}{2}\sqrt{2a^2 + 2c^2 - b^2}$$ $$m_c = \frac{1}{2}\sqrt{2a^2 + 2b^2 - c^2}$$
Apollonius-Theorem:
$$a^2 + b^2 + c^2 = \frac{4}{3}(m_a^2 + m_b^2 + m_c^2)$$
Fläche aus Medianen:
$$A = \frac{4}{3}\sqrt{s_m(s_m-m_a)(s_m-m_b)(s_m-m_c)}$$ wobei $s_m = \frac{m_a + m_b + m_c}{2}$ der Halbumfang der Medianen ist.
Umfang:
$$U = a + b + c$$

Beispielrechnung

Beispiel mit Seiten a = 5 cm, b = 6 cm, c = 7 cm:

Median m_a berechnen:
$m_a = \frac{1}{2}\sqrt{2b^2 + 2c^2 - a^2}$
$m_a = \frac{1}{2}\sqrt{2 \times 6^2 + 2 \times 7^2 - 5^2}$
$m_a = \frac{1}{2}\sqrt{72 + 98 - 25} = \frac{1}{2}\sqrt{145} \approx 6{,}02$ cm

Median m_b berechnen:
$m_b = \frac{1}{2}\sqrt{2 \times 5^2 + 2 \times 7^2 - 6^2}$
$m_b = \frac{1}{2}\sqrt{50 + 98 - 36} = \frac{1}{2}\sqrt{112} \approx 5{,}29$ cm

Median m_c berechnen:
$m_c = \frac{1}{2}\sqrt{2 \times 5^2 + 2 \times 6^2 - 7^2}$
$m_c = \frac{1}{2}\sqrt{50 + 72 - 49} = \frac{1}{2}\sqrt{73} \approx 4{,}27$ cm

Fläche berechnen (Heron):
$s = \frac{5 + 6 + 7}{2} = 9$
$A = \sqrt{9 \times (9-5) \times (9-6) \times (9-7)} = \sqrt{9 \times 4 \times 3 \times 2} = \sqrt{216} \approx 14{,}70$ cm²

Apollonius-Theorem prüfen:
$a^2 + b^2 + c^2 = 25 + 36 + 49 = 110$
$\frac{4}{3}(m_a^2 + m_b^2 + m_c^2) = \frac{4}{3}(36{,}24 + 27{,}99 + 18{,}24) \approx 109{,}96$ ✓

Rückrechnungsformeln

Umkehrformeln:

Seiten aus Medianen:
• $a = \sqrt{\frac{4}{3}(m_b^2 + m_c^2) - \frac{4}{3} \cdot m_a^2}$
• $b = \sqrt{\frac{4}{3}(m_a^2 + m_c^2) - \frac{4}{3} \cdot m_b^2}$
• $c = \sqrt{\frac{4}{3}(m_a^2 + m_b^2) - \frac{4}{3} \cdot m_c^2}$

Alternative Darstellung:
• $a^2 = \frac{4}{3}\left(m_b^2 + m_c^2 - \frac{m_a^2}{2}\right)$
• $b^2 = \frac{4}{3}\left(m_a^2 + m_c^2 - \frac{m_b^2}{2}\right)$
• $c^2 = \frac{4}{3}\left(m_a^2 + m_b^2 - \frac{m_c^2}{2}\right)$

Der Schwerpunkt (Zentroid)

Eigenschaften des Schwerpunkts:

Schnittpunkt aller drei Seitenhalbierenden
Teilt jede Median im Verhältnis 2:1 vom Eckpunkt aus
Schwerpunkt ist der Massenmittelpunkt bei gleichmäßiger Massenverteilung
Koordinaten: $S = \left(\frac{x_A + x_B + x_C}{3}, \frac{y_A + y_B + y_C}{3}\right)$

Abstände vom Schwerpunkt:

Vom Eckpunkt zur Seitenmitte: $\frac{2}{3}$ der Medianlänge
Vom Schwerpunkt zur Seitenmitte: $\frac{1}{3}$ der Medianlänge
Der Schwerpunkt liegt immer innerhalb des Dreiecks

Besondere Dreiecke und ihre Medianen

Gleichseitiges Dreieck:

Alle Medianen gleich lang: $m_a = m_b = m_c = \frac{a\sqrt{3}}{2}$
Medianen sind gleichzeitig Höhen und Winkelhalbierende
Schwerpunkt = Umkreismittelpunkt = Inkreismittelpunkt

Gleichschenkliges Dreieck ($a = b$):

Zwei Medianen gleich lang: $m_a = m_b$
Median zur Basis ist gleichzeitig Höhe und Symmetrieachse
Schwerpunkt liegt auf der Symmetrieachse

Rechtwinkliges Dreieck:

Median zur Hypotenuse: $m_c = \frac{c}{2}$ (halbe Hypotenuse)
Dies ist eine besondere Eigenschaft rechtwinkliger Dreiecke
Schwerpunkt liegt nicht im Umkreismittelpunkt

Praktische Anwendungen

Statik & Mechanik

• Schwerpunktbestimmung und Gleichgewicht
• Stabilitätsberechnungen und Lastverteilung
• Massenträgheitsmomente und Balancierung
• Mechanik starrer Körper

Technik & Computergrafik

• Triangulation und Flächenberechnung
• Mesh-Generierung und Polygon-Verarbeitung
• Vermessung und Landvermessung
• CAD-Systeme und technische Zeichnungen

Seitenhalbierenden und Schwerpunkt sind wichtig in:

Statik: Schwerpunktbestimmung, Gleichgewicht
Architektur: Stabilitätsberechnungen, Lastverteilung
Maschinenbau: Massenträgheitsmomente, Balancierung
Computergrafik: Triangulation, Flächenberechnung
Vermessung: Flächenteilung, Landvermessung
Physik: Mechanik starrer Körper, Rotationsdynamik

Interessante Eigenschaften

Varignon'sches Parallelogramm:

Verbindet man die Mittelpunkte der Seiten, entsteht ein Parallelogramm
Dieses Parallelogramm hat die halbe Fläche des ursprünglichen Dreiecks
Die Diagonalen dieses Parallelogramms sind Medianen des Dreiecks

Flächenteilung durch Medianen:

Jede Median teilt das Dreieck in zwei kongruente Hälften
Alle drei Medianen zusammen teilen das Dreieck in 6 kleinere Dreiecke
Diese 6 Dreiecke haben alle die gleiche Fläche (je $\frac{1}{6}$ der Gesamtfläche)

Seitenhalbierenden - Zentrale Dreieckslinien:

Schwerpunkt: Alle drei Medianen treffen sich in einem zentralen Punkt
Teilungsverhältnis: Schwerpunkt teilt jede Median im Verhältnis 2:1
Flächenteilung: Jede Median halbiert die Dreiecksfläche perfekt
Praktische Relevanz: Von Statik bis Computergrafik universell wichtig
Mathematische Eleganz: Apollonius-Theorem und klare Formeln

Geometrie Rechner 2D Runde Formen

Kreis

Dreiecke

Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)

Spezielle Vierecke

Quadrat
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt

Polygone

N-Eck (Universal)
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)

Allgemeine Vierecke

Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)