Raute Rechner

Online Rechner für alle Berechnungen an der Raute (Rhombus)


🔸 Raute Rechner

Gleichseitig - Diagonalen rechtwinklig

Einheiten
Einheiten
Einheiten
°
Einheiten²
Einheiten
Einheiten
Einheiten
ℹ️
Hinweis: Geben Sie mindestens zwei Werte ein. Der Rechner berechnet alle anderen Eigenschaften der Raute automatisch.
⚠️ Fehler:

Geben Sie mindestens zwei bekannte Werte ein. Der Rechner berechnet automatisch alle anderen Eigenschaften der Raute (Rhombus).

Eingabeformat

• Dezimalzahlen mit Punkt oder Komma
• Winkel in Grad (0° bis 180°)
• Mindestens zwei Werte erforderlich

Beste Eingabkombinationen:

  • Beide Diagonalen: Vollständige Berechnung aller Eigenschaften
  • Seitenlänge + Winkel: Alle Eigenschaften berechenbar
  • Seitenlänge + Fläche/Höhe: Bestimmung der restlichen Werte

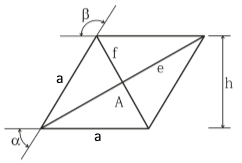
Raute


Die Raute (Rhombus)

Eine Raute (auch Rhombus genannt) ist ein spezielles Parallelogramm, bei dem alle vier Seiten gleich lang sind. Sie ist ein vielseitiges geometrisches Objekt mit besonderen Eigenschaften und findet in vielen Bereichen Anwendung.

🔸 Eigenschaften
  • • Alle Seiten gleich lang: a = b = c = d
  • • Gegenüberliegende Winkel gleich: α = γ und β = δ
  • • Benachbarte Winkel supplementär: α + β = 180°
  • • Punktsymmetrie: zum Diagonalenschnittpunkt
📐 Diagonalen-Eigenschaften
  • • Halbieren sich rechtwinklig: e ⊥ f
  • • Sind Symmetrieachsen der Raute
  • • Teilen in 4 kongruente rechtwinklige Dreiecke
  • • Pythagorasbeziehung: e² + f² = 4a²

Grundlegende Formeln

📊 Formeln für die Raute:

Fläche:
$$A = \frac{e \cdot f}{2} = a^2 \cdot \sin(\alpha) = a \cdot h$$
Umfang:
$$U = 4a$$
Diagonalen:
$$e = 2a \cdot \cos\left(\frac{\alpha}{2}\right), \quad f = 2a \cdot \sin\left(\frac{\alpha}{2}\right)$$
Seitenlänge aus Diagonalen:
$$a = \frac{1}{2}\sqrt{e^2 + f^2}$$
Höhe und Inkreisradius:
$$h = a \cdot \sin(\alpha) = \frac{A}{a}, \quad r = \frac{A}{2a}$$

Beispielrechnung

📝 Beispielrechnung: e = 8 cm, f = 6 cm

Seitenlänge berechnen:
$a = \frac{1}{2}\sqrt{e^2 + f^2} = \frac{1}{2}\sqrt{8^2 + 6^2} = \frac{1}{2}\sqrt{100} = 5$ cm

Fläche berechnen:
$A = \frac{e \cdot f}{2} = \frac{8 \cdot 6}{2} = 24$ cm²

Umfang berechnen:
$U = 4a = 4 \cdot 5 = 20$ cm

Winkel berechnen:
$\tan(\alpha/2) = \frac{f}{e} = \frac{6}{8} = 0{,}75$
$\alpha \approx 73{,}74°$, $\beta \approx 106{,}26°$

Höhe und Inkreisradius:
$h = \frac{A}{a} = \frac{24}{5} = 4{,}8$ cm
$r = \frac{A}{2a} = \frac{24}{10} = 2{,}4$ cm

Spezialfälle der Raute

🔲 Quadrat (α = 90°)
  • • Alle Winkel sind rechte Winkel
  • • Diagonalen sind gleich lang
  • • e = f = a√2
  • • 4 Symmetrieachsen statt 2
🔸 Gleichseitige Raute (α = 60°)
  • • Kann in 6 gleichseitige Dreiecke geteilt werden
  • • e = a√3, f = a
  • • Besondere Beziehungen zu Hexagonen
  • • Optimale Bienenwaben-Struktur
📏 Sehr flache Raute (α → 0°)
  • • Eine Diagonale wird sehr lang
  • • Die andere Diagonale wird sehr kurz
  • • Höhe geht gegen 0
  • • Fläche geht gegen 0
  • • Form wird linienähnlich
  • • Umfang bleibt konstant

Praktische Anwendungen

🏗️ Technik & Ingenieurwesen
  • • Fachwerk-Konstruktionen
  • • Gitternetzstrukturen
  • • Kristallgitter (Rhomboedrisch)
  • • Mechanische Verbindungen
🏛️ Architektur & Design
  • • Fliesenmuster und Parkettierungen
  • • Fenster- und Türformen
  • • Moderne Architektur
  • • Ornamente und Verzierungen
🔬 Natur & Wissenschaft
  • • Kristallstrukturen (Calcit, Dolomit)
  • • Molekülgeometrie
  • • Bienenwaben-ähnliche Strukturen
  • • Optische Anwendungen (Rhombusprismen)
🎨 Alltag & Kunst
  • • Spielkarten (Karo-Symbol)
  • • Logos und Grafiken
  • • Textile Muster
  • • Schmuck und Edelsteine
🌟 Die Raute - Geometrische Eleganz:
  • Perfekte Symmetrie: 2 Achsen + Punktsymmetrie
  • Diagonale Orthogonalität: Rechtwinklige Halbierung
  • Vielseitige Anwendung: Von Kristallen bis Kunst
  • Mathematische Schönheit: Elegante Formeln und Beziehungen
Geometrie Rechner 2D Runde Formen
Kreis
Dreiecke
Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)
Spezielle Vierecke
Quadrat
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt
Polygone
N-Eck (Universal)
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)
Allgemeine Vierecke
Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)