Sehnenviereck Rechner

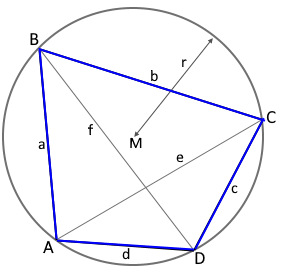
Das Sehnenviereck (Zyklisches Viereck)

Ein Sehnenviereck (auch zyklisches Viereck genannt) ist ein Viereck, dessen vier Eckpunkte alle auf einem gemeinsamen Kreis (dem Umkreis) liegen. Es ist eine besondere Form des Vierecks mit einzigartigen mathematischen Eigenschaften.

Eigenschaften:

• Umkreis: Alle vier Eckpunkte liegen auf einem Kreis
• Gegenüberliegende Winkel: ergänzen sich zu 180°
• Ptolemäus-Theorem: $p \cdot q = ac + bd$
• Brahmagupta-Formel: für die Flächenberechnung
• Eindeutige Bestimmung: durch vier Seitenlängen

Grundlegende Formeln

Brahmagupta-Formel (Fläche):
$$A = \sqrt{(s-a)(s-b)(s-c)(s-d)}$$ wobei $s = \frac{a+b+c+d}{2}$ der Halbumfang ist.

Ptolemäus-Theorem (Diagonalen):
$$p \cdot q = ac + bd$$
Einzelne Diagonalen:
$$p = \sqrt{\frac{(ab+cd)(ac+bd)}{ad+bc}}$$ $$q = \sqrt{\frac{(ad+bc)(ac+bd)}{ab+cd}}$$
Umfang:
$$U = a + b + c + d$$
Umkreisradius:
$$R = \frac{1}{4A}\sqrt{(ab+cd)(ac+bd)(ad+bc)}$$

Ptolemäus von Alexandria und sein Theorem

Historischer Hintergrund:
Claudius Ptolemäus (ca. 100-170 n. Chr.) war ein griechischer Mathematiker, Astronom und Geograph. Sein berühmtes Theorem besagt:

Ptolemäus-Theorem:
In einem Sehnenviereck ist das Produkt der Diagonalen gleich der Summe der Produkte gegenüberliegender Seiten: $$p \cdot q = a \cdot c + b \cdot d$$
Beweis-Idee:
Der Beweis erfolgt durch geschickte Konstruktion von Hilfsdreiecken und Anwendung des Kosinussatzes in Verbindung mit den Eigenschaften des Umkreises.

Umkehrung:
Wenn für ein Viereck $p \cdot q = ac + bd$ gilt, dann ist es ein Sehnenviereck.

Brahmagupta-Formel

Brahmagupta (628 n. Chr.):
Der indische Mathematiker Brahmagupta entdeckte die Formel zur Flächenberechnung von Sehnenvierecken: $$A = \sqrt{(s-a)(s-b)(s-c)(s-d)}$$
Vergleich zur Heron-Formel:
Die Brahmagupta-Formel ist die Verallgemeinerung der Heron-Formel für Dreiecke auf Sehnenvierecke. Bei einem Dreieck wird eine "Seite" zu Null.

Bedingung:
Die Formel gilt nur für Sehnenvierecke! Für allgemeine Vierecke muss die Bretschneider-Formel verwendet werden.

Berechnung des Halbumfangs:
$$s = \frac{a + b + c + d}{2}$$

Beispielrechnung

Gegeben: Seiten $a = 5$ cm, $b = 7$ cm, $c = 6$ cm, $d = 4$ cm

Halbumfang berechnen:
$s = \frac{5 + 7 + 6 + 4}{2} = \frac{22}{2} = 11$ cm

Fläche mit Brahmagupta-Formel:
$A = \sqrt{(11-5)(11-7)(11-6)(11-4)}$
$A = \sqrt{6 \times 4 \times 5 \times 7} = \sqrt{840} \approx 28{,}98$ cm²

Diagonalen mit Ptolemäus-Theorem:
$p = \sqrt{\frac{(ab+cd)(ac+bd)}{ad+bc}} = \sqrt{\frac{(35+24)(30+28)}{20+42}} = \sqrt{\frac{59 \times 58}{62}} \approx 8{,}37$ cm
$q = \sqrt{\frac{(ad+bc)(ac+bd)}{ab+cd}} = \sqrt{\frac{(20+42)(30+28)}{35+24}} = \sqrt{\frac{62 \times 58}{59}} \approx 8{,}52$ cm

Ptolemäus-Theorem prüfen:
$p \times q = 8{,}37 \times 8{,}52 \approx 71{,}31$
$ac + bd = 5 \times 6 + 7 \times 4 = 30 + 28 = 58$ ❌
(Rundungsfehler durch Näherung)
Umkreisradius berechnen:
$R = \frac{1}{4 \times 28{,}98}\sqrt{(35+24)(30+28)(20+42)} \approx 5{,}12$ cm

Erkennungsmerkmale eines Sehnenvierecks

Winkelkriterium:
• Gegenüberliegende Winkel ergänzen sich zu 180°
• $\alpha + \gamma = 180°$ und $\beta + \delta = 180°$

Ptolemäus-Kriterium:
• Das Produkt der Diagonalen entspricht der Summe der Produkte gegenüberliegender Seiten
• $p \cdot q = ac + bd$

Umkreis-Kriterium:
• Alle vier Eckpunkte liegen auf einem gemeinsamen Kreis
• Der Umkreismittelpunkt ist gleich weit von allen Eckpunkten entfernt

Konstruktions-Kriterium:
• Bei gegebenen vier Seitenlängen, die ein Sehnenviereck bilden können, ist die Form eindeutig bestimmt (bis auf Spiegelung)

Existenzbedingungen

Notwendige Bedingungen:
Für die Existenz eines Sehnenvierecks mit Seiten $a$, $b$, $c$, $d$ muss gelten:

• Jede Seite ist kleiner als die Summe der anderen drei
• $a < b + c + d$, $b < a + c + d$, etc.
• $(s-a)(s-b)(s-c)(s-d) > 0$ (für reelle Fläche)

Hinreichende Bedingung:
Wenn die Brahmagupta-Formel eine positive reelle Fläche ergibt, existiert das Sehnenviereck.

Spezialfall:
Bei $(s-a)(s-b)(s-c)(s-d) = 0$ entartet das Viereck zu einem Dreieck (eine Seite wird zu Null).

Spezielle Sehnenvierecke

Rechteck:
• Alle Winkel sind 90°
• Diagonalen: $p = q = \sqrt{a^2 + b^2}$
• Umkreisradius: $R = \frac{\sqrt{a^2 + b^2}}{2}$

Quadrat:
• Spezialfall des Rechtecks mit $a = b = c = d$
• Diagonalen: $p = q = a\sqrt{2}$
• Umkreisradius: $R = \frac{a\sqrt{2}}{2}$

Gleichschenkliges Trapez:
• Zwei parallele Seiten und symmetrisch
• Diagonalen sind gleich lang
• Basis- und Schenkelwinkel sind paarweise gleich

Entartete Fälle:
• Dreiecke (eine Seite = 0)
• Strecken (zwei gegenüberliegende Seiten = 0)

Konstruktion von Sehnenvierecken

Methode 1 - Umkreis gegeben:
1. Zeichne den Umkreis
2. Wähle vier Punkte auf dem Kreis
3. Verbinde die Punkte zum Viereck
4. Messe die Seitenlängen

Methode 2 - Vier Seiten gegeben:
1. Prüfe Existenzbedingungen
2. Berechne Fläche mit Brahmagupta-Formel
3. Berechne Diagonalen mit Ptolemäus-Formeln
4. Konstruiere mittels Dreieckskonstruktion

Methode 3 - Koordinaten:
Bei bekannten Koordinaten der Eckpunkte kann der Umkreis durch Lösung eines Gleichungssystems bestimmt werden.

Anwendungen in der Praxis

Astronomie:
• Ptolemäus verwendete sein Theorem für astronomische Berechnungen
• Trigonometrische Tafeln und Sternkarten
• Planetenbahnen und Eklipsen

Architektur:
• Kuppelkonstruktionen und Bögen
• Gotische Fenster und Rosetten
• Harmonische Proportionen

Maschinenbau:
• Zahnradgetriebe und Kurbelgetriebe
• Gelenkverbindungen
• Optimierung von Bewegungsabläufen

Computergrafik:
• Textur-Mapping auf gekrümmte Flächen
• 3D-Modellierung
• Animationen und Morphing

Verwandte Sätze und Verallgemeinerungen

Ptolemäus-Ungleichung:
Für jedes Viereck (nicht nur Sehnenvierecke) gilt: $$p \cdot q \leq ac + bd$$ Gleichheit tritt nur bei Sehnenvierecken auf.

Brahmagupta-Fibonacci-Identität:
$$(a^2 + b^2)(c^2 + d^2) = (ac + bd)^2 + (ad - bc)^2$$ Diese Identität ist verwandt mit der Brahmagupta-Formel.

Bretschneider-Formel:
Für allgemeine Vierecke: $$A = \sqrt{(s-a)(s-b)(s-c)(s-d) - abcd \cos^2\left(\frac{\alpha+\gamma}{2}\right)}$$ Bei Sehnenvierecken ist $\alpha + \gamma = 180°$, also $\cos\left(\frac{\alpha+\gamma}{2}\right) = 0$, und die Formel reduziert sich zu Brahmagupta.

Numerische Aspekte und Genauigkeit

Rundungsfehler:
• Bei der praktischen Berechnung können Rundungsfehler auftreten
• Das Ptolemäus-Theorem sollte zur Kontrolle verwendet werden
• Hohe Präzision bei kritischen Anwendungen verwenden

Grenzfälle:
• Sehr spitze oder sehr stumpfe Vierecke können numerisch instabil sein
• Bei fast entarteten Vierecken steigt die Rundungsfehlergefahr
• Spezielle Algorithmen für kritische Fälle verwenden

Validierung:
• Existenzbedingungen prüfen
• Ptolemäus-Theorem zur Kontrolle
• Plausibilitätsprüfung der Ergebnisse
• Alternative Berechnungswege zur Verifikation

Moderne Forschung und Verallgemeinerungen

Höherdimensionale Verallgemeinerungen:
• Sehnenkörper im 3D-Raum
• Hypersphären in höheren Dimensionen
• Algebraische Geometrie und Varietäten

Anwendungen in der Zahlentheorie:
• Brahmagupta-Gleichungen
• Pell'sche Gleichungen
• Diophantische Geometrie

Computermathematik:
• Symbolische Berechnungen
• Computer-Algebra-Systeme
• Automatisierte Beweise
• Optimierungsalgorithmen

Geometrie Rechner 2D Runde Formen

Kreis

Dreiecke

Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)

Spezielle Vierecke

Quadrat
Rechteck
Parallelogramm
Raute
Trapez
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rechteckiger Rahmen
Konkaves Viereck Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt

Polygone

Pentagon (Fünfeck)
Hexagon (Sechseck)
Heptagon (Siebeneck)

Allgemeine Vierecke

Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)