Quadrat Rechner

Online Rechner für alle Berechnungen am Quadrat


🔲 Quadrat Rechner

Perfekte Symmetrie - Vier gleiche Seiten & Winkel

Einheiten
Einheiten
Einheiten²
Einheiten
Einheiten
Einheiten
ℹ️
Hinweis: Geben Sie genau einen Wert ein. Der Rechner berechnet alle anderen Eigenschaften des Quadrats automatisch.
⚠️ Fehler:

Geben Sie einen bekannten Wert ein. Der Rechner berechnet automatisch alle anderen Eigenschaften des Quadrats.

Eingabeformat

Dezimalzahlen können mit Punkt oder Komma eingegeben werden. Geben Sie nur einen Wert ein - alle anderen werden berechnet.

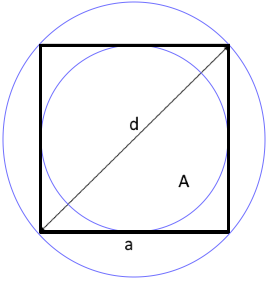
Quadrat


Das Quadrat - Perfekte Symmetrie

Ein Quadrat ist ein spezielles Rechteck, bei dem alle vier Seiten gleich lang sind und alle vier Winkel rechte Winkel (90°) betragen. Es ist die regelmäßigste Form unter den Vierecken und hat besondere mathematische Eigenschaften.

🔲 Perfekte Eigenschaften
  • • Alle Seiten gleich: a = b = c = d
  • • Alle Winkel gleich: α = β = γ = δ = 90°
  • • 4 Symmetrieachsen
  • • Punktsymmetrie zum Mittelpunkt
📐 Diagonalen-Eigenschaften
  • • Gleich lang: d₁ = d₂ = a√2
  • • Rechtwinklig: schneiden sich bei 90°
  • • Halbieren sich im Mittelpunkt
  • • 4 kongruente Dreiecke

Grundlegende Formeln

📊 Alle Berechnungen basieren auf der Seitenlänge a:

Diagonale:
$$d = a \cdot \sqrt{2} \approx 1{,}414 \times a$$
Fläche:
$$A = a^2 = \frac{d^2}{2}$$
Umfang:
$$U = 4 \times a$$
Inkreisradius:
$$r = \frac{a}{2}$$
Umkreisradius:
$$R = \frac{a \sqrt{2}}{2} = \frac{d}{2}$$

Rückrechnungsformeln

🔄 Seitenlänge aus anderen Werten berechnen:

Aus Diagonale:
$$a = \frac{d}{\sqrt{2}} = \frac{d\sqrt{2}}{2}$$
Aus Fläche:
$$a = \sqrt{A}$$
Aus Umfang:
$$a = \frac{U}{4}$$
Aus Inkreisradius:
$$a = 2r$$
Aus Umkreisradius:
$$a = R\sqrt{2}$$

Praktische Beispiele

📝 Beispielrechnung: Quadrat mit a = 5 cm

Diagonale berechnen:
$d = a \times \sqrt{2} = 5 \times 1{,}414 \approx 7{,}07$ cm

Fläche berechnen:
$A = a^2 = 5^2 = 25$ cm²

Umfang berechnen:
$U = 4 \times a = 4 \times 5 = 20$ cm

Inkreisradius berechnen:
$r = \frac{a}{2} = \frac{5}{2} = 2{,}5$ cm

Umkreisradius berechnen:
$R = \frac{a \times \sqrt{2}}{2} = \frac{5 \times 1{,}414}{2} \approx 3{,}54$ cm

Besondere Verhältnisse

Das Quadrat zeigt bemerkenswerte mathematische Verhältnisse:

Geometrische Verhältnisse:
• Umkreisradius : Inkreisradius = √2 : 1 ≈ 1,414 : 1
• Diagonale : Seitenlänge = √2 : 1 ≈ 1,414 : 1
• Umkreisfläche : Quadratfläche = π : 2 ≈ 1,571 : 1
• Quadratfläche : Inkreisfläche = 4 : π ≈ 1,273 : 1

Optimierungseigenschaft:
Das Quadrat hat bei gegebenem Umfang die größte Fläche aller Rechtecke und bei gegebener Fläche den kleinsten Umfang.

Symmetrie-Eigenschaften:
• 4 Symmetrieachsen (2 Mittellinien + 2 Diagonalen)
• 4-zählige Rotationssymmetrie (90°, 180°, 270°)
• Punkt-, Achsen- und Drehsymmetrie vereint

Spezielle Berechnungen

⚖️ Verhältnisse zu eingeschriebenen Kreisen

Zum Inkreis (berührt alle 4 Seiten):
• Radius: $r = \frac{a}{2}$
• Fläche Quadrat : Fläche Inkreis = $4 : \pi \approx 1{,}273$
• Umfang Quadrat : Umfang Inkreis = $4 : \pi \approx 1{,}273$

Zum Umkreis (durch alle 4 Ecken):
• Radius: $R = \frac{a\sqrt{2}}{2}$
• Fläche Umkreis : Fläche Quadrat = $\pi : 2 \approx 1{,}571$
• Die Eckpunkte des Quadrats liegen auf dem Umkreis

Diagonalen-Eigenschaften:
• Länge: $d = a\sqrt{2}$
• Teilen das Quadrat in 4 kongruente rechtwinklige Dreiecke
• Schneiden sich rechtwinklig im Mittelpunkt

Praktische Anwendungen

🏗️ Architektur & Bau
  • • Grundrisse und Räume
  • • Fenster und Türen
  • • Fliesen und Kacheln
  • • Stadtplätze
⚙️ Technik & Industrie
  • • Schraubenköpfe (Vierkant)
  • • Flansche und Profile
  • • Elektronik-Platinen
  • • Präzisionsbauteile
🎨 Kunst & Design
  • • Bildformate (1:1)
  • • Muster und Ornamente
  • • Grafisches Design
  • • Symmetrische Layouts
💻 Mathematik & IT
  • • Koordinatensysteme
  • • Pixel und Displays
  • • QR-Codes
  • • Spielfelder (Schach)
🌟 Das Quadrat als perfekte Form:
  • Maximale Symmetrie: 4 Achsen + Punkt- + Drehsymmetrie
  • Optimale Effizienz: Größte Fläche bei kleinstem Umfang
  • Einfache Berechnung: Alle Formeln basieren auf einer Seitenlänge
  • Universelle Anwendung: Von Architektur bis Informatik
Geometrie Rechner 2D Runde Formen
Kreis
Dreiecke
Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)
Spezielle Vierecke
Quadrat
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt
Polygone
N-Eck (Universal)
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)
Allgemeine Vierecke
Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)