Goldenes Rechteck Rechner

Online Rechner für das Goldene Rechteck mit dem Goldenen Schnitt


🟨 Goldenes Rechteck Rechner

Goldener Schnitt φ = 1,618... - Perfekte Proportionen

💡 Goldenes Rechteck: Das Verhältnis ist immer φ = 1,618... (Goldener Schnitt)
📏 Rechteck-Eigenschaften
Einheiten
Einheiten
Einheiten²
Einheiten
Einheiten
⚠️ Fehler:

Geben Sie einen bekannten Wert ein. Der Rechner berechnet automatisch alle anderen Eigenschaften des Goldenen Rechtecks basierend auf φ = 1,618...

Besonderheiten

• Das Verhältnis ist immer φ ≈ 1,618
• Basiert auf dem Goldenen Schnitt
• Perfekte ästhetische Proportionen
• Natürliche Harmonie

Goldener Schnitt φ

• Definition: φ = (1 + √5)/2
• Wert: φ ≈ 1,6180339887...
• Eigenschaft: φ² = φ + 1

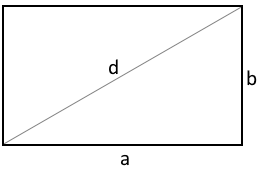
Goldenes Rechteck


Das Goldene Rechteck

Das Goldene Rechteck ist ein spezielles Rechteck, dessen Seitenverhältnis dem Goldenen Schnitt entspricht. Das Verhältnis der langen zur kurzen Seite beträgt exakt φ ≈ 1,618..., eine der wichtigsten mathematischen Konstanten in der Natur und Kunst.

🟨 Goldenes Rechteck Eigenschaften
  • • Goldenes Verhältnis: a/b = φ = 1,618...
  • • Selbstähnlichkeit: Unendliche Teilbarkeit
  • • Fibonacci-Beziehung: Grenzwert der Verhältnisse
  • • Natürliche Harmonie: Ästhetisch perfekt
🔄 Mathematische Eigenschaften
  • • φ² = φ + 1: Einzigartige algebraische Eigenschaft
  • • 1/φ = φ - 1: Reziproke Beziehung
  • • Kettenbruch: Einfachste irrationale Zahl
  • • Goldene Spirale: Logarithmische Spirale

  • Goldenes Verhältnis: $\frac{a}{b} = \phi = \frac{1 + \sqrt{5}}{2}$
  • Selbstähnlichkeit: Entfernt man ein Quadrat, bleibt wieder ein Goldenes Rechteck
  • Fibonacci-Beziehung: Entsteht aus Fibonacci-Rechtecken
  • Goldene Spirale: Kann eine perfekte logarithmische Spirale einschreiben
  • Ästhetische Perfektion: Als besonders harmonisch empfunden


Der Goldene Schnitt φ (Phi)

📊 Definition und Eigenschaften:

Definition des Goldenen Schnitts:
$$\phi = \frac{1 + \sqrt{5}}{2} = 1{,}6180339887...$$
Algebraische Eigenschaften:
$$\phi^2 = \phi + 1 = 2{,}618...$$ $$\frac{1}{\phi} = \phi - 1 = 0{,}618...$$
Kettenbruchdarstellung:
$$\phi = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \ddots}}}$$

Formeln für das Goldene Rechteck

📐 Berechnungsformeln:

Mit der langen Seite $a$ als Basis:

Kurze Seite:
$$b = \frac{a}{\phi} = a \cdot (\phi - 1) = a \cdot 0{,}618...$$
Fläche:
$$A = a \cdot b = a \cdot \frac{a}{\phi} = \frac{a^2}{\phi}$$
Umfang:
$$U = 2(a + b) = 2a\left(1 + \frac{1}{\phi}\right) = 2a \cdot \phi$$
Diagonale:
$$d = \sqrt{a^2 + b^2} = a\sqrt{1 + \frac{1}{\phi^2}} = a\sqrt{\frac{\phi^2 + 1}{\phi^2}}$$

Rückrechnungsformeln

🔄 Umkehrformeln:

Lange Seite aus anderen Werten:
• Aus kurzer Seite: $a = b \cdot \phi$
• Aus Fläche: $a = \sqrt{A \cdot \phi}$
• Aus Umfang: $a = \frac{U}{2\phi}$
• Aus Diagonale: $a = d \cdot \sqrt{\frac{\phi^2}{\phi^2 + 1}}$
Kurze Seite aus anderen Werten:
• Aus langer Seite: $b = \frac{a}{\phi}$
• Aus Fläche: $b = \sqrt{\frac{A}{\phi}}$
• Aus Umfang: $b = \frac{U}{2\phi^2}$
• Aus Diagonale: $b = d \cdot \sqrt{\frac{1}{\phi^2 + 1}}$

Beispielrechnung

📝 Beispiel mit a = 10 cm:

Kurze Seite berechnen:
$b = \frac{a}{\phi} = \frac{10}{1{,}618} \approx 6{,}18$ cm

Verhältnis überprüfen:
$\frac{a}{b} = \frac{10}{6{,}18} \approx 1{,}618 = \phi$ ✓

Fläche berechnen:
$A = a \times b = 10 \times 6{,}18 = 61{,}8$ cm²

Umfang berechnen:
$U = 2(a + b) = 2(10 + 6{,}18) = 32{,}36$ cm

Diagonale berechnen:
$d = \sqrt{a^2 + b^2} = \sqrt{10^2 + 6{,}18^2} = \sqrt{100 + 38{,}19} \approx 11{,}76$ cm

Fibonacci-Verbindung

Fibonacci-Folge: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

Grenzwert der Verhältnisse:
$$\lim_{n \to \infty} \frac{F_{n+1}}{F_n} = \phi$$
Beispiele: $\frac{8}{5} = 1{,}6$, $\frac{13}{8} = 1{,}625$, $\frac{21}{13} = 1{,}615$, $\frac{34}{21} = 1{,}619$

Fibonacci-Rechtecke:
Rechtecke mit Fibonacci-Zahlen als Seitenlängen nähern sich immer mehr dem Goldenen Rechteck an.

Konstruktion des Goldenen Rechtecks

🏗️ Klassische Konstruktion
  1. Zeichne ein Quadrat mit Seitenlänge 1
  2. Halbiere eine Seite und zeichne zur gegenüberliegenden Ecke
  3. Diese Strecke hat die Länge √5/2
  4. Verlängere um 1/2 → Gesamtlänge φ
  5. Konstruiere das Rechteck mit Seiten 1 und φ
🔄 Die Goldene Spirale
  • • Teile das Goldene Rechteck durch ein Quadrat
  • • Das verbleibende Rechteck ist wieder golden
  • • Wiederhole diesen Prozess unendlich
  • • Zeichne Viertelkreise in jedes Quadrat
  • • Ergebnis: Logarithmische Spirale

Vorkommen in der Natur

Das Goldene Rechteck und der Goldene Schnitt finden sich überall in der Natur:

  • Pflanzen: Blattanordnung, Blütenblätter, Samenstände (Sonnenblumen)
  • Tiere: Schneckenhäuser, Nautilus-Gehäuse, Körperproportionen
  • Kristalle: Pentagonale Symmetrien, Quasikristalle
  • Galaxien: Spiralarme folgen oft der Goldenen Spirale
  • Menschlicher Körper: Gesichtsproportionen, Fingerlängen

Anwendungen in Kunst und Architektur

Historische Bauwerke:

  • Parthenon: Fassadenproportionen folgen dem Goldenen Schnitt
  • Pyramiden: Seitenverhältnisse basieren auf φ
  • Gotische Kathedralen: Höhe-zu-Breite-Verhältnisse
  • Renaissance-Kunst: Leonardo da Vinci, Michelangelo

Moderne Anwendungen:
  • Design: Logos, Layouts, Webdesign
  • Fotografie: Bildkomposition, Drittel-Regel
  • Architektur: Le Corbusier's Modulor
  • Produktdesign: Apple-Produkte, Automobildesign

Warum wirkt das Goldene Rechteck ästhetisch?

Psychologische Aspekte:
• Das menschliche Auge empfindet φ-Proportionen als besonders harmonisch
• Weder zu "quadratisch" noch zu "schmal"
• Optimales Verhältnis für Lesbarkeit und Wahrnehmung

Evolutionäre Theorie:
• Menschen sind evolutionär an natürliche Proportionen gewöhnt
• Goldene Verhältnisse kommen häufig in der Natur vor
• Verbindung zu Fibonacci-Mustern in Pflanzen und Tieren

Mathematische Schönheit:
• Eindeutige Definition durch irrationale Zahl
• Selbstähnlichkeit und Rekursion
• Verbindung zu fundamentalen mathematischen Konzepten

Moderne wissenschaftliche Forschung

Quasikristalle:
2011 erhielt Dan Shechtman den Nobelpreis für die Entdeckung von Quasikristallen, die pentagonale Symmetrien und den Goldenen Schnitt aufweisen.

Biophysik:
Neuere Forschungen zeigen φ-Verhältnisse in:
• DNA-Strukturen
• Proteinfalten
• Neuronalen Netzwerken
• Herzrhythmus-Variabilität

Kosmologie:
Einige Theorien diskutieren φ im Zusammenhang mit:
• Dunkler Energie
• Universellen Konstanten
• Fraktaler Geometrie des Universums

Praktische Anwendungen heute

Webdesign und UI/UX:
• Responsive Layouts mit φ-Proportionen
• Goldene Ratio Typography
• Spacing und Margins

Investmentstrategien:
• Fibonacci-Retracements in der Technischen Analyse
• φ-basierte Handelssignale
• Risiko-Management-Verhältnisse

Algorithmen und Optimierung:
• Golden Section Search
• Fibonacci-Heap Datenstrukturen
• Optimierung von Suchtiefen

🌟 Das Goldene Rechteck - Perfekte Harmonie:
  • Mathematische Vollkommenheit: Basiert auf der faszinierendsten irrationalen Zahl φ
  • Natürliche Schönheit: Überall in der Natur zu finden
  • Kulturelle Bedeutung: Grundlage für Kunst und Architektur seit Jahrtausenden
  • Moderne Relevanz: Von Webdesign bis zu wissenschaftlichen Entdeckungen
  • Universelle Harmonie: Verbindet Mathematik, Natur und menschliche Wahrnehmung
Geometrie Rechner 2D Runde Formen
Kreis
Dreiecke
Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)
Spezielle Vierecke
Quadrat
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt
Polygone
N-Eck (Universal)
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)
Allgemeine Vierecke
Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)