Drachenviereck Rechner

Online Rechner für Drachenvierecke (Deltoide) und Tangentenvierecke


🪁 Drachenviereck Rechner

Symmetrische Deltoide & Tangentenvierecke mit Inkreis

Einheiten
Einheiten
Einheiten
🪁
Drachenviereck: A = ½ × p × q | Inkreis vorhanden | Diagonalen senkrecht
⚠️ Fehler:

Geben Sie die beiden Diagonalen p und q sowie den Überstand c des Drachenvierecks ein. Der Rechner berechnet alle anderen Eigenschaften wie Seiten, Winkel, Fläche und Inkreisradius.

Eingaberegeln

• Hauptdiagonale p und Nebendiagonale q
• Überstand c (Abstand vom Mittelpunkt zur Spitze)
• Dezimalzahlen mit Punkt oder Komma
• Alle Werte müssen positiv sein

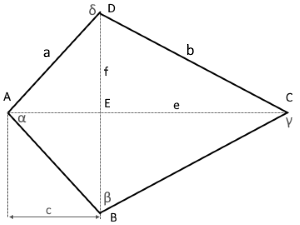
Drachenviereck mit Bezeichnungen

Drachenviereck-Eigenschaften

• Symmetrie: Achsensymmetrisch zur Hauptdiagonale
• Tangentenviereck: Inkreis vorhanden
• Senkrechte Diagonalen: p ⊥ q


Das Drachenviereck (Deltoid)

Ein Drachenviereck (auch Deltoid oder Tangentenviereck genannt) ist ein symmetrisches Viereck mit zwei Paaren gleich langer benachbarter Seiten. Es ist sowohl ein spezielles Tangentenviereck (besitzt einen Inkreis) als auch ein wichtiges Element in der Geometrie.

🪁 Drachenviereck-Eigenschaften
  • • Symmetrie: Achsensymmetrisch zur p-Diagonale
  • • Seitenpaare: a = a (kurz), b = b (lang)
  • • Senkrechte Diagonalen: p ⊥ q
  • • Tangentenviereck: Inkreis vorhanden

📐 Berechnungsgrundlagen
  • • Fläche: A = ½ × p × q
  • • Umfang: U = 2(a + b)
  • • Inkreis: r = A/s (s = Halbumfang)
  • • Winkel: α + β = 180° (supplementär)

Charakteristische Eigenschaften:

  • Zwei Seitenpaare: a = a (kurze Seiten), b = b (lange Seiten)
  • Achsensymmetrie: Eine Symmetrieachse durch die Hauptdiagonale
  • Senkrechte Diagonalen: Diagonalen stehen im rechten Winkel zueinander
  • Inkreis: Besitzt einen einbeschriebenen Kreis (Tangentenviereck)


Grundlegende Formeln

🪁 Drachenviereck Formeln:

Flächenberechnung:
$$A = \frac{1}{2} \cdot p \cdot q$$ wobei $p$ und $q$ die beiden Diagonalen sind.
Alternative Flächenformel:
$$A = r \cdot s = r \cdot \frac{a + b}{1}$$ wobei $r$ der Inkreisradius und $s$ der Halbumfang ist.
Umfang:
$$U = 2(a + b) = 2a + 2b$$
Inkreisradius:
$$r = \frac{A}{s} = \frac{p \cdot q}{2(a + b)}$$
Diagonalen aus Seiten:
$$p^2 = a^2 + b^2 + 2ab\cos(\alpha)$$ $$q^2 = a^2 + b^2 - 2ab\cos(\alpha)$$

Winkeleigenschaften

📐 Winkel-Berechnungen:

Winkel alpha:
$$\alpha = \arccos\left(\frac{2a^2 - q^2}{2a^2}\right)$$
Winkel beta:
$$\beta = \arccos\left(\frac{a^2 + b^2 - p^2}{2ab}\right)$$
Winkel gamma:
$$\gamma = \arccos\left(\frac{2b^2 - q^2}{2b^2}\right)$$
Winkelsumme:
$$\alpha + 2\beta + \gamma = 360°$$
Beziehung zu den Diagonalen:
$$\tan\left(\frac{\alpha}{2}\right) = \frac{q}{p} \cdot \frac{b}{a}$$
Cosinussatz für Drachenvierecke:
$$p^2 = (a + b)^2 - 4ab\sin^2\left(\frac{\alpha}{2}\right)$$ $$q^2 = (a - b)^2 + 4ab\cos^2\left(\frac{\alpha}{2}\right)$$

Beispielrechnung

📝 Beispiel mit a = 5 cm, b = 8 cm und α = 60°:

Winkel beta:
$\beta = \arccos\left(\frac{a^2 + b^2 - p^2}{2ab}\right)$

Umfang:
$U = 2(a + b) = 2(5 + 8) = 26$ cm

Fläche:
$A = \frac{1}{2} \cdot p \cdot q = \frac{1}{2} \cdot 11{,}36 \cdot 7 \approx 39{,}76$ cm²

Inkreisradius:
$r = \frac{A}{s} = \frac{39{,}76}{13} \approx 3{,}06$ cm

Konstruktionsverfahren

Methode 1 - Aus Seiten und Winkel:
1. Zeichne die Hauptdiagonale $p$ als Symmetrieachse
2. Markiere den Mittelpunkt und teile $p$ im Verhältnis der Seitenlängen
3. Konstruiere die Nebendiagonale $q$ senkrecht zu $p$
4. Verbinde die vier Eckpunkte

Methode 2 - Aus Diagonalen:
1. Zeichne beide Diagonalen senkrecht zueinander
2. Die Hauptdiagonale $p$ wird nicht halbiert
3. Die Nebendiagonale $q$ wird durch die Hauptdiagonale halbiert
4. Bestimme die Schnittpunkte und verbinde die Eckpunkte

Methode 3 - Inkreis-Konstruktion:
1. Konstruiere den Inkreis mit Radius $r$
2. Zeichne vier Tangenten an den Kreis
3. Zwei Tangenten sind parallel (für a-Seiten)
4. Zwei weitere Tangenten sind parallel (für b-Seiten)
5. Die Schnittpunkte bilden das Drachenviereck

Mathematische Eigenschaften

Symmetrie-Eigenschaften:
• Eine Spiegelachse (Hauptdiagonale)
• Keine Punktsymmetrie (außer bei Raute)
• Drehsymmetrie nur bei speziellen Fällen

Diagonal-Eigenschaften:
• Diagonalen stehen senkrecht zueinander
• Hauptdiagonale ist Symmetrieachse
• Nebendiagonale wird von Hauptdiagonale halbiert
• Hauptdiagonale wird im Allgemeinen nicht halbiert

Flächenteilung:
Die Hauptdiagonale teilt das Drachenviereck in zwei kongruente Dreiecke:
$$A_1 = A_2 = \frac{1}{2} \cdot \frac{p}{2} \cdot q = \frac{pq}{4}$$
Inkreis-Beziehungen:
$$\text{Berührpunkte teilen die Seiten im Verhältnis:}$$ $$\frac{t_a}{a-t_a} = \frac{r}{\sqrt{a^2-r^2}}$$ wobei $t_a$ der Abstand vom Eckpunkt zum Berührpunkt ist

Praktische Anwendungen

🏗️ Architektur & Design
  • • Dachformen und Giebelkonstruktionen
  • • Fensterformen in gotischer Architektur
  • • Moderne Designelemente
  • • Kachel- und Pflastermuster
⚙️ Technik & Maschinenbau
  • • Zahnradprofile und Nockenformen
  • • Aerodynamische Profile (Tragflächen)
  • • Optische Linsen und Prismen
  • • Getriebe und Kupplungselemente

Natur und Biologie:
• Blattformen vieler Pflanzen
• Schmetterlingsflügel und Insektenformen
• Kristallstrukturen in Mineralogie
• Zellanordnungen in biologischen Geweben

Kunst und Handwerk:
• Schmuckdesign und Edelsteinschliff
• Textilmuster und Webarten
• Kalligrafie und Schriftgestaltung
• Origami und Papierfalttechniken

Berechnungsfehler vermeiden

Häufige Fallstricke:
• Verwechslung von Haupt- und Nebendiagonale
• Falsche Annahme über Diagonalenhalbierung
• Vertauschung von spitzem und stumpfem Winkel
• Vergessen der Senkrechteigenschaft der Diagonalen

Validierungsregeln:
• $\alpha + \beta = 180°$ (Supplementärität)
• $a < b$ für typische Drachenvierecke
• $p \perp q$ (Diagonalen senkrecht)
• $A = rs$ (Tangentenviereck-Eigenschaft)

Grenzfälle beachten:
• Bei $a = b$ entsteht eine Raute
• Bei $\alpha = 90°$ entsteht ein Rechteck
• Bei $a = b$ und $\alpha = 90°$ entsteht ein Quadrat
• Bei sehr spitzen Winkeln können numerische Probleme auftreten

Historische Bedeutung

Antike Mathematik:
• Erwähnung bei Euklid in den "Elementen"
• Verwendung in babylonischen und ägyptischen Berechnungen
• Bedeutung für frühe Feldmessungen

Mittelalterliche Geometrie:
• Rolle in der islamischen Mathematik
• Anwendung in der Kathedralgeometrie
• Verwendung in der Astronomie

Moderne Entwicklungen:
• Verbindung zur projektiven Geometrie
• Anwendungen in der Computergrafik
• Rolle in der Kristallographie
• Bedeutung für moderne Designtheorie

🌟 Drachenviereck - Symmetrische Perfektion:
  • Achsensymmetrie: Spiegelachse durch die Hauptdiagonale
  • Tangentenviereck: Inkreis mit speziellen Eigenschaften
  • Vielseitige Anwendung: Von Architektur bis Naturformen
  • Einfache Berechnung: Klare Formeln für alle Eigenschaften
  • Natürliche Harmonie: Häufig in Natur und Design zu finden
Geometrie Rechner 2D Runde Formen
Kreis
Dreiecke
Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)
Spezielle Vierecke
Quadrat
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt
Polygone
N-Eck (Universal)
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)
Allgemeine Vierecke
Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)