Gleichseitiges Dreieck Rechner

Online Rechner für alle Berechnungen am gleichseitigen Dreieck

Eingabe (einen Wert eingeben):

Seitenlänge ($a$)

Höhe ($h$)

Fläche ($A$)

Umfang ($U$)

Inkreisradius ($r$)

Umkreisradius ($R$)

Dezimalstellen

Seitenlänge ($a$)

Höhe ($h$)

Fläche ($A$)

Umfang ($U$)

Inkreisradius ($r$)

Umkreisradius ($R$)

Geben Sie einen bekannten Wert ein. Der Rechner berechnet automatisch alle anderen Eigenschaften des gleichseitigen Dreiecks.

Eingabeformat

Dezimalzahlen können mit Punkt oder Komma eingegeben werden. Geben Sie nur einen Wert ein - alle anderen werden berechnet.

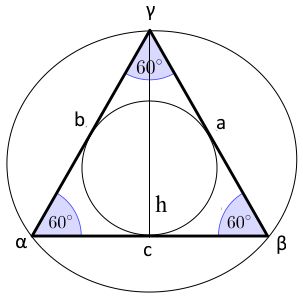
gleichseitiges Dreieck

Das gleichseitige Dreieck

Ein gleichseitiges Dreieck ist ein spezielles Dreieck, bei dem alle drei Seiten gleich lang sind. Es ist perfekt symmetrisch und hat besondere mathematische Eigenschaften. Alle Innenwinkel betragen genau 60°.

Eigenschaften:

Alle Seiten gleich lang: $a = b = c$
Alle Winkel gleich: $\alpha = \beta = \gamma = 60°$
Drei Symmetrieachsen: durch jede Ecke und Seitenmitte
Inkreis und Umkreis: haben gemeinsamen Mittelpunkt

Formeln für das gleichseitige Dreieck

Alle Berechnungen basieren auf der Seitenlänge $a$:

Höhe:
$$h = \frac{a \cdot \sqrt{3}}{2}$$
Fläche:
$$A = \frac{a^2 \cdot \sqrt{3}}{4}$$
Umfang:
$$U = 3 \cdot a$$
Inkreisradius:
$$r = \frac{a \cdot \sqrt{3}}{6} = \frac{h}{3}$$
Umkreisradius:
$$R = \frac{a \cdot \sqrt{3}}{3} = \frac{2h}{3}$$

Beispielrechnung

Gegeben: Seitenlänge $a = 6$ cm

Höhe berechnen:
$h = \frac{6 \times \sqrt{3}}{2} = \frac{6 \times 1{,}732}{2} \approx 5{,}20$ cm

Fläche berechnen:
$A = \frac{6^2 \times \sqrt{3}}{4} = \frac{36 \times 1{,}732}{4} \approx 15{,}59$ cm²

Umfang berechnen:
$U = 3 \times 6 = 18$ cm

Inkreisradius berechnen:
$r = \frac{6 \times \sqrt{3}}{6} = \sqrt{3} \approx 1{,}73$ cm

Umkreisradius berechnen:
$R = \frac{6 \times \sqrt{3}}{3} = 2\sqrt{3} \approx 3{,}46$ cm

Rückrechnungsformeln

Seitenlänge aus anderen Werten:
• Aus Höhe: $a = \frac{2h}{\sqrt{3}}$
• Aus Fläche: $a = \sqrt{\frac{4A}{\sqrt{3}}}$
• Aus Umfang: $a = \frac{U}{3}$
• Aus Inkreisradius: $a = \frac{6r}{\sqrt{3}}$
• Aus Umkreisradius: $a = \frac{3R}{\sqrt{3}}$

Besondere Eigenschaften

Symmetrie:

Das gleichseitige Dreieck hat 3 Symmetrieachsen
Es ist punktsymmetrisch zum Schwerpunkt
Schwerpunkt, Umkreismittelpunkt und Inkreismittelpunkt fallen zusammen

Verhältnisse:

Umkreisradius : Inkreisradius = $2 : 1$
Höhe : Inkreisradius = $3 : 1$
Das Verhältnis von Fläche zu Umfang² ist maximal unter allen Dreiecken

Praktische Anwendungen

Gleichseitige Dreiecke finden sich in vielen Bereichen:

Architektur: Geodätische Kuppeln, Dachkonstruktionen
Technik: Wabenstrukturen, Fachwerke
Kristallographie: Hexagonale Kristallstrukturen
Design: Logos, Muster, Ornamente
Natur: Bienenwaben, Schneeflocken

Geometrie Rechner 2D Runde Formen

Kreis

Dreiecke

Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)

Spezielle Vierecke

Quadrat
Rechteck
Parallelogramm
Raute
Trapez
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rechteckiger Rahmen
Konkaves Viereck Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt

Polygone

Pentagon (Fünfeck)
Hexagon (Sechseck)
Heptagon (Siebeneck)

Allgemeine Vierecke

Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)