Heptagon Rechner

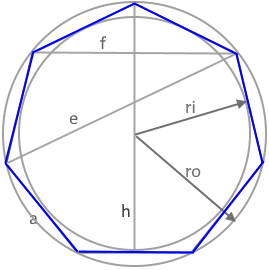
Das Heptagon (Regelmäßiges Siebeneck)

Ein Heptagon ist ein regelmäßiges Siebeneck mit sieben gleichen Seiten und sieben gleichen Innenwinkeln. Es ist ein besonderes Polygon, da es nicht mit Zirkel und Lineal konstruierbar ist, sondern nur näherungsweise oder mit speziellen Verfahren.

Eigenschaften:

• Sieben gleiche Seiten: alle Seiten haben die Länge $a$
• Sieben gleiche Innenwinkel: jeder Winkel beträgt $\frac{5 \cdot 180°}{7} \approx 128{,}57°$
• Sieben Symmetrieachsen: durch jede Ecke und Seitenmitte
• 7-zählige Rotationssymmetrie: alle $\frac{360°}{7} \approx 51{,}43°$ identisch
• Besonderheit: Nicht mit klassischen Mitteln konstruierbar

width="280" height="280" align="right" />

Grundlegende Formeln

Alle Berechnungen basieren auf der Seitenlänge $a$:

Innenwinkel:
$$\alpha = \frac{(7-2) \times 180°}{7} = \frac{900°}{7} \approx 128{,}57°$$
Kurze Diagonale (über eine Ecke):
$$d_1 = 2a \cos(\pi/7) \approx 1{,}802 \times a$$
Lange Diagonale (über zwei Ecken):
$$d_2 = \frac{a \sin(3\pi/7)}{\sin(\pi/7)} \approx 2{,}247 \times a$$
Fläche:
$$A = \frac{7a^2}{4 \tan(\pi/7)} \approx 3{,}634 \times a^2$$
Umfang:
$$U = 7a$$
Inkreisradius:
$$r = \frac{a}{2 \tan(\pi/7)} \approx 1{,}038 \times a$$
Umkreisradius:
$$R = \frac{a}{2 \sin(\pi/7)} \approx 1{,}152 \times a$$

Konstruierbarkeit und Geschichte

Das regelmäßige Heptagon ist ein besonderes Polygon, da es nicht mit Zirkel und Lineal konstruierbar ist.

Gaußsche Theorie:
Nach Carl Friedrich Gauß ist ein regelmäßiges n-Eck nur dann mit Zirkel und Lineal konstruierbar, wenn n das Produkt einer Zweierpotenz und verschiedener Fermat-Primzahlen ist. Da 7 eine normale Primzahl (keine Fermat-Primzahl) ist, ist das Heptagon nicht konstruierbar.

Näherungskonstruktionen:
Obwohl nicht exakt konstruierbar, gibt es verschiedene Näherungsverfahren:

• Archimedes-Methode mit Spiralen
• Neusis-Konstruktionen (mit markiertem Lineal)
• Iterative Verfahren
• Trigonometrische Näherungen

Rückrechnungsformeln

Seitenlänge aus anderen Werten:
• Aus kurzer Diagonale: $$a = \frac{d_1}{2 \cos(\pi/7)} \approx 0{,}555 \times d_1$$
• Aus langer Diagonale: $$a = \frac{d_2 \sin(\pi/7)}{\sin(3\pi/7)} \approx 0{,}445 \times d_2$$
• Aus Fläche: $$a = \sqrt{\frac{4A \tan(\pi/7)}{7}} \approx 0{,}525 \times \sqrt{A}$$
• Aus Umfang: $$a = \frac{U}{7}$$
• Aus Inkreisradius: $$a = 2r \tan(\pi/7) \approx 0{,}963 \times r$$
• Aus Umkreisradius: $$a = 2R \sin(\pi/7) \approx 0{,}868 \times R$$

Näherungskonstruktion

Praktische Konstruktion (Näherung):

1. Zeichne einen Kreis mit Mittelpunkt O
2. Teile den Umfang in 7 gleiche Teile (je ≈ 51,43°)
3. Verwende dazu: $\frac{360°}{7} \approx 51{,}43°$
4. Verbinde die 7 Punkte zu einem regelmäßigen Siebeneck

Alternative Methode (Archimedes):

• Verwende die Beziehung $\sin(\pi/7) \approx 0{,}4339$
• Konstruiere rechtwinklige Dreiecke mit diesem Verhältnis
• Übertrage die Seitenlängen auf den Umkreis

Beispielrechnung

Gegeben: Seitenlänge $a = 5$ cm

Kurze Diagonale berechnen:
$d_1 = a \times 1{,}802 = 5 \times 1{,}802 \approx 9{,}01$ cm

Lange Diagonale berechnen:
$d_2 = a \times 2{,}247 = 5 \times 2{,}247 \approx 11{,}24$ cm

Fläche berechnen:
$A = 3{,}634 \times a^2 = 3{,}634 \times 25 \approx 90{,}85$ cm²

Umfang berechnen:
$U = 7 \times a = 7 \times 5 = 35$ cm

Inkreisradius berechnen:
$r = 1{,}038 \times a = 1{,}038 \times 5 \approx 5{,}19$ cm

Umkreisradius berechnen:
$R = 1{,}152 \times a = 1{,}152 \times 5 \approx 5{,}76$ cm

Praktische Anwendungen

Heptagone finden sich seltener als andere Polygone, haben aber spezielle Anwendungen:

• Münzen: Britische 50-Pence- und 20-Pence-Münzen (Reuleaux-Heptagon)
• Architektur: Spezielle Kuppeln und Grundrisse
• Kristallographie: Seltene, aber existierende Kristallformen
• Design: Logos und künstlerische Muster
• Natur: Sehr seltene Blütenformen
• Technik: Spezielle Getriebe und Werkzeuge

Mathematische Besonderheiten

Algebraische Eigenschaften:
Das Heptagon ist mit der Gleichung 7. Grades verbunden und kann nicht durch Quadratwurzeln ausgedrückt werden.

Trigonometrische Beziehungen:
$$\cos\left(\frac{2\pi}{7}\right) = \frac{\sqrt{7} - 1}{4} - \frac{\sqrt{2(7-\sqrt{7})}}{4}$$ Diese komplexe Formel zeigt die algebraische Komplexität des Heptagons.

Unmöglichkeit der Parkettierung:
Regelmäßige Heptagone können die Ebene nicht lückenlos füllen, da $128{,}57°$ kein ganzzahliger Teiler von $360°$ ist.

Verwandte Polygone

Andere regelmäßige Polygone:

• Dreieck (3 Seiten): $\alpha = 60°$ - konstruierbar
• Quadrat (4 Seiten): $\alpha = 90°$ - konstruierbar
• Pentagon (5 Seiten): $\alpha = 108°$ - konstruierbar
• Hexagon (6 Seiten): $\alpha = 120°$ - konstruierbar
• Heptagon (7 Seiten): $\alpha \approx 128{,}57°$ - nicht konstruierbar
• Octagon (8 Seiten): $\alpha = 135°$ - konstruierbar

Konstruierbarkeitsregel:
Ein regelmäßiges n-Eck ist genau dann konstruierbar, wenn $n = 2^k \cdot p_1 \cdot p_2 \cdot ... \cdot p_r$, wobei $p_i$ verschiedene Fermat-Primzahlen sind.

Historisches und Kulturelles

Antike Mathematik:
Bereits die alten Griechen erkannten die besonderen Schwierigkeiten beim Heptagon. Archimedes entwickelte Näherungsverfahren.

Moderne Mathematik:
Gauß bewies 1796 die Unmöglichkeit der Konstruktion mit Zirkel und Lineal. Dies war ein Meilenstein der algebraischen Geometrie.

Symbolik:

• Zahl 7 als mystische Zahl in vielen Kulturen
• Wochentage, Weltwunder, Tugenden
• Seltene Verwendung in Architektur und Design
• Symbol für Vollkommenheit und Vollständigkeit

Geometrie Rechner 2D Runde Formen

Kreis

Dreiecke

Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)

Spezielle Vierecke

Quadrat
Rechteck
Parallelogramm
Raute
Trapez
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rechteckiger Rahmen
Konkaves Viereck Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt

Polygone

Pentagon (Fünfeck)
Hexagon (Sechseck)
Heptagon (Siebeneck)

Allgemeine Vierecke

Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)