Viereck im Koordinatensystem Rechner

Online Rechner für allgemeine Vierecke - Berechnung von Seitenlängen, Diagonalen, Fläche und Umfang


📐 Viereck Koordinaten Rechner

Allgemeine Vierecke - Aus Eckpunkt-Koordinaten

x
y
x
y
x
y
x
y
ℹ️
Hinweis: Geben Sie die Koordinaten der vier Eckpunkte ein. Die Punkte sollten in Reihenfolge (im oder gegen den Uhrzeigersinn) eingegeben werden.
⚠️ Fehler:

Geben Sie die Koordinaten der vier Eckpunkte des Vierecks ein. Die Punkte sollten in Reihenfolge (im oder gegen den Uhrzeigersinn) eingegeben werden.

Eingaberegeln

• Koordinaten als Dezimalzahlen eingeben
• Punkt oder Komma als Dezimaltrennzeichen
• Negative Koordinaten sind möglich
• Die vier Punkte dürfen nicht kollinear sein

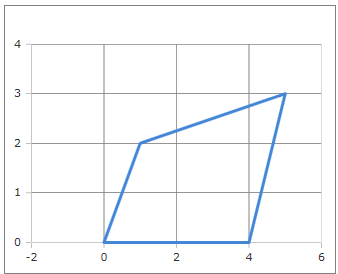
Viereck


Das allgemeine Viereck

Ein allgemeines Viereck (auch unregelmäßiges Viereck genannt) ist ein Polygon mit vier Ecken und vier Seiten, bei dem keine besonderen Symmetrien oder Parallelitäten vorausgesetzt werden. Durch die Koordinaten der vier Eckpunkte wird das Viereck eindeutig bestimmt.

📍 Koordinaten-Eigenschaften
  • • Vier Eckpunkte: A(xₐ, yₐ), B(xᵦ, yᵦ), C(xᶜ, yᶜ), D(xᴅ, yᴅ)
  • • Vier Seiten: AB, BC, CD, DA
  • • Zwei Diagonalen: AC und BD
  • • Winkelsumme: Die Summe aller Innenwinkel beträgt 360°
🧮 Berechnungsverfahren
  • • Seitenlängen: Abstandsformel zwischen Punkten
  • • Diagonalen: Direkte Koordinatenberechnung
  • • Fläche: Shoelace-Formel (Gauß-Formel)
  • • Umfang: Summe aller Seitenlängen

Formeln für das allgemeine Viereck

📊 Grundlegende Berechnungsformeln:

Seitenlängen (Abstandsformel):
$$AB = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2}$$ $$BC = \sqrt{(x_C - x_B)^2 + (y_C - y_B)^2}$$ $$CD = \sqrt{(x_D - x_C)^2 + (y_D - y_C)^2}$$ $$DA = \sqrt{(x_A - x_D)^2 + (y_A - y_D)^2}$$
Diagonalen:
$$AC = \sqrt{(x_C - x_A)^2 + (y_C - y_A)^2}$$ $$BD = \sqrt{(x_D - x_B)^2 + (y_D - y_B)^2}$$
Umfang:
$$U = AB + BC + CD + DA$$
Fläche (Shoelace-Formel):
$$A = \frac{1}{2} |x_A(y_B - y_D) + x_B(y_C - y_A) + x_C(y_D - y_B) + x_D(y_A - y_C)|$$

Alternative Flächenformeln

🔺 Verschiedene Berechnungsverfahren

Teilung in Dreiecke:
Das Viereck kann in zwei Dreiecke geteilt werden. Die Gesamtfläche ist die Summe der Dreiecksflächen: $$A = A_{\triangle ABC} + A_{\triangle ACD}$$
Mit Kreuzprodukt:
$$A_{\triangle ABC} = \frac{1}{2} |(x_B - x_A)(y_C - y_A) - (x_C - x_A)(y_B - y_A)|$$ $$A_{\triangle ACD} = \frac{1}{2} |(x_C - x_A)(y_D - y_A) - (x_D - x_A)(y_C - y_A)|$$
Determinanten-Formel:
$$A = \frac{1}{2} \left| \det \begin{pmatrix} x_A & y_A & 1 \\ x_B & y_B & 1 \\ x_C & y_C & 1 \end{pmatrix} + \det \begin{pmatrix} x_A & y_A & 1 \\ x_C & y_C & 1 \\ x_D & y_D & 1 \end{pmatrix} \right|$$

Beispielrechnung

📝 Beispielrechnung: Viereck mit Koordinaten

Gegeben: $A(0, 0)$, $B(4, 0)$, $C(5, 3)$, $D(1, 2)$

Seitenlängen berechnen:
$AB = \sqrt{(4-0)^2 + (0-0)^2} = \sqrt{16} = 4$
$BC = \sqrt{(5-4)^2 + (3-0)^2} = \sqrt{1 + 9} = \sqrt{10} \approx 3{,}16$
$CD = \sqrt{(1-5)^2 + (2-3)^2} = \sqrt{16 + 1} = \sqrt{17} \approx 4{,}12$
$DA = \sqrt{(0-1)^2 + (0-2)^2} = \sqrt{1 + 4} = \sqrt{5} \approx 2{,}24$

Diagonalen berechnen:
$AC = \sqrt{(5-0)^2 + (3-0)^2} = \sqrt{25 + 9} = \sqrt{34} \approx 5{,}83$
$BD = \sqrt{(1-4)^2 + (2-0)^2} = \sqrt{9 + 4} = \sqrt{13} \approx 3{,}61$

Umfang berechnen:
$U = 4 + 3{,}16 + 4{,}12 + 2{,}24 = 13{,}52$

Fläche berechnen (Shoelace):
$A = \frac{1}{2} |0(0-2) + 4(3-0) + 5(2-0) + 1(0-3)|$
$A = \frac{1}{2} |0 + 12 + 10 - 3| = \frac{1}{2} \cdot 19 = 9{,}5$

Spezielle Viereckstypen

Das allgemeine Viereck kann verschiedene Spezialformen annehmen:

Konvexes Viereck:
• Alle Innenwinkel sind kleiner als 180°
• Keine Selbstüberschneidungen
• Diagonalen liegen vollständig im Inneren

Konkaves Viereck:
• Mindestens ein Innenwinkel größer als 180°
• Eine oder beide Diagonalen verlaufen außerhalb
• "Eingedellte" Form

Trapez:
• Ein Paar parallele Seiten
• Spezialfall des allgemeinen Vierecks

Parallelogramm:
• Zwei Paare parallele Seiten
• Gegenüberliegende Seiten gleich lang

Besondere Eigenschaften

Orientierung prüfen:
Die Orientierung der Eckpunkte (im oder gegen den Uhrzeigersinn) beeinflusst das Vorzeichen der Flächenberechnung:

  • Positives Ergebnis: Eckpunkte gegen den Uhrzeigersinn
  • Negatives Ergebnis: Eckpunkte im Uhrzeigersinn
  • Für die Fläche wird der Betrag verwendet

Selbstüberschneidung erkennen:
• Ein Viereck überschneidet sich selbst, wenn sich zwei nicht benachbarte Seiten schneiden
• Dies kann durch Prüfung der Schnittpunkte der Seiten erkannt werden
• Selbstüberschneidende Vierecke haben komplexere Flächenberechnungen

Validierung der Eingabe

Wichtige Prüfungen:

  • Eindeutigkeit: Alle vier Punkte müssen verschieden sein
  • Kollinearität: Nicht alle Punkte dürfen auf einer Geraden liegen
  • Reihenfolge: Die Punkte sollten in korrekter Reihenfolge eingegeben werden
  • Orientierung: Für korrekte Flächenberechnung beachten

Häufige Fehlerquellen:
• Falsche Reihenfolge der Eckpunkte
• Doppelte Punkte
• Alle Punkte auf einer Linie
• Selbstüberschneidung nicht erkannt

Praktische Anwendungen

Allgemeine Vierecke finden Anwendung in:

  • Computergrafik: Polygon-Rendering, Textur-Mapping
  • CAD-Systeme: Freiform-Flächenmodellierung
  • Vermessung: Grundstücksflächen, unregelmäßige Parzellen
  • Architektur: Atypische Grundrisse, moderne Bauformen
  • Kartographie: Verwaltungsgrenzen, Gebietsaufteilung
  • Spielentwicklung: Kollisionserkennung, Level-Design
  • Robotik: Pfadplanung in komplexen Umgebungen

Erweiterte Berechnungen

Schwerpunkt (Zentroid):
$$S = \left(\frac{x_A + x_B + x_C + x_D}{4}, \frac{y_A + y_B + y_C + y_D}{4}\right)$$
Mittelpunkt der Diagonalen:
$$M_{AC} = \left(\frac{x_A + x_C}{2}, \frac{y_A + y_C}{2}\right)$$ $$M_{BD} = \left(\frac{x_B + x_D}{2}, \frac{y_B + y_D}{2}\right)$$
Winkel berechnen:
Die Innenwinkel können mit Vektorrechnung bestimmt werden: $$\cos(\angle ABC) = \frac{\vec{BA} \cdot \vec{BC}}{|\vec{BA}| \cdot |\vec{BC}|}$$

Koordinatentransformationen

Translation (Verschiebung):
$$A'(x_A + \Delta x, y_A + \Delta y), B'(x_B + \Delta x, y_B + \Delta y), ...$$
Rotation um den Ursprung:
$$x' = x \cos \theta - y \sin \theta$$ $$y' = x \sin \theta + y \cos \theta$$
Skalierung:
$$x' = s_x \cdot x, \quad y' = s_y \cdot y$$
Diese Transformationen ändern die Form und Größe des Vierecks, aber die grundlegenden Berechnungsformeln bleiben gleich.

🌟 Koordinaten-basierte Viereck-Berechnung:
  • Exakte Berechnung: Alle Werte direkt aus Koordinaten
  • Flexible Eingabe: Beliebige Viereck-Formen möglich
  • Robuste Formeln: Shoelace-Verfahren für Flächenberechnung
  • Universell anwendbar: Von Vermessung bis Computergrafik
Geometrie Rechner 2D Runde Formen
Kreis
Dreiecke
Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)
Spezielle Vierecke
Quadrat
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt
Polygone
N-Eck (Universal)
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)
Allgemeine Vierecke
Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)