Dreigleichseitiges Trapez Rechner

Online Rechner für Trapeze mit drei gleichen Seiten


🔷 Dreigleichseitiges Trapez Rechner

Drei gleiche Seiten - Maximale Symmetrie

💡 Besonderheit: Drei Seiten sind gleich lang (b = c = d)! Nur Basis a ist unterschiedlich.
Einheiten
Einheiten
ℹ️
Bedingung: Die Basis a muss größer als b/3 sein, damit ein gültiges Trapez entsteht!
⚠️ Fehler:

Geben Sie nur zwei Werte ein: die untere Basis a und die Länge b der drei gleichen Seiten. Der Rechner berechnet automatisch alle anderen Eigenschaften.

Eingaberegeln

• Basis a (untere parallele Seite)
• Seite b (obere Basis c = Schenkel d = b)
• Dezimalzahlen mit Punkt oder Komma
• a muss größer als b/3 sein

Dreigleichseitige Eigenschaften

• Drei gleiche Seiten: b = c = d
• Symmetrisch: α = β und γ = δ
• Umkreis vorhanden: als Sehnenviereck
• Gleiche Diagonalen: p = q

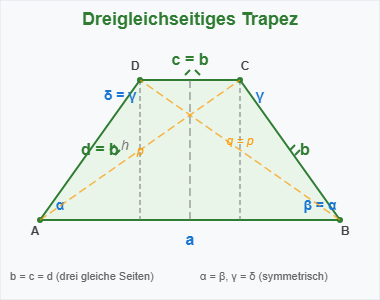
Dreigleichseitiges Trapez mit Bezeichnungen


Das dreigleichseitige Trapez - Trapez mit drei gleichen Seiten

Ein dreigleichseitiges Trapez ist eine sehr spezielle Form des Trapezes, bei dem drei der vier Seiten gleich lang sind: die obere Basis c und beide Schenkel b und d haben dieselbe Länge. Dies ist ein äußerst seltener und mathematisch interessanter Fall.

🔷 Dreigleichseitige Merkmale
  • • Drei gleiche Seiten: b = c = d
  • • Gleichschenklig: Automatisch symmetrisch
  • • Gleiche Basiswinkel: α = β
  • • Gleiche obere Winkel: γ = δ
🔵 Besondere Eigenschaften
  • • Gleiche Diagonalen: p = q
  • • Umkreis existiert: Sehnenviereck
  • • Maximale Symmetrie: Zwei Achsen
  • • Nur 2 Parameter: a und b

Grundlegende Formeln

📊 Formeln für das dreigleichseitige Trapez:

Bedingung:
$$b = c = d \quad \text{und} \quad a > \frac{b}{3}$$
Höhenberechnung:
$$h = \sqrt{b^2 - \left(\frac{a-b}{2}\right)^2}$$
Winkelberechnung:
$$\alpha = \beta = \arcsin\left(\frac{h}{b}\right), \quad \gamma = \delta = 180° - \alpha$$
Flächenberechnung:
$$A = \frac{1}{2} \cdot (a + b) \cdot h$$
Umfang (besonders einfach):
$$U = a + 3b$$
Umkreisradius (speziell):
$$R = b \cdot \sqrt{\frac{b(a + b)}{4b^2 - (a - b)^2}}$$

Praktisches Berechnungsbeispiel

📝 Beispielrechnung: a = 12 cm, b = 5 cm

Prüfung der Bedingung:
$a > \frac{b}{3} \Rightarrow 12 > \frac{5}{3} = 1{,}67$ ✓

Drei gleiche Seiten:
$c = d = b = 5$ cm

Höhe berechnen:
$h = \sqrt{5^2 - \left(\frac{12-5}{2}\right)^2} = \sqrt{25 - 12{,}25} = 3{,}57$ cm

Winkel berechnen:
$\alpha = \beta = \arcsin\left(\frac{3{,}57}{5}\right) = 45{,}23°$
$\gamma = \delta = 180° - 45{,}23° = 134{,}77°$

Fläche:
$A = \frac{(12 + 5) \times 3{,}57}{2} = 30{,}35$ cm²

Umfang (einfach):
$U = 12 + 3 \times 5 = 27$ cm

Diagonalen (gleich):
$p = q = \sqrt{3{,}57^2 + 8{,}5^2} = 9{,}22$ cm

Umkreisradius:
$R = 5 \cdot \sqrt{\frac{5 \times 17}{4 \times 25 - 49}} = 6{,}46$ cm

Geometrische Analyse und Bedingungen

📏 Existenzbedingungen
  • • Grundbedingung: a > b > 0
  • • Geometrische Machbarkeit: b > (a-b)/2
  • • Vereinfacht: a > b/3
  • • Grenzfall: Bei a = b/3 wird h = 0
🎯 Optimierungseigenschaften
  • • Minimale Parameter: Nur 2 statt 4
  • • Eindeutige Lösung: (a,b) → alle Werte
  • • Maximale Symmetrie: Zwei Achsen
  • • Sehnenviereck: Umkreis existiert

Praktische Anwendungen

🏗️ Konstruktive Anwendungen
  • • Symmetrische Dachformen
  • • Standardisierte Profile
  • • Optische Prismen
  • • Geometrische Designs
🔬 Mathematische Bedeutung
  • • Spezialfall der Trapez-Theorie
  • • Verbindung Dreieck-Rechteck
  • • Optimierungsbeispiel
  • • Hochsymmetrische Formen
🌟 Das dreigleichseitige Trapez - Geometrische Rarität:
  • Einzigartige Eigenschaft: Drei von vier Seiten sind identisch
  • Maximale Symmetrie: Sowohl achsen- als auch punktsymmetrisch
  • Minimale Komplexität: Nur zwei Parameter bestimmen alles
  • Sehnenviereck: Umkreis existiert mit spezieller Formel
  • Praktische Relevanz: Ideal für standardisierte symmetrische Konstruktionen
Geometrie Rechner 2D Runde Formen
Kreis
Dreiecke
Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)
Spezielle Vierecke
Quadrat
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt
Polygone
N-Eck (Universal)
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)
Allgemeine Vierecke
Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)