Pfeilviereck Rechner

Online Rechner für pfeilförmige konkave Vierecke


➤ Pfeilviereck Rechner

Pfeilförmige konkave Vierecke mit Navigation & Richtung

Einheiten
°
°
°
➤
Pfeilviereck: Spitzenwinkel α + Reflexwinkel β > 180° = charakteristische Pfeilform
⚠️ Fehler:

Geben Sie eine Seitenlänge und 2 Winkel des Pfeilvierecks ein. Der Rechner berechnet automatisch alle Eigenschaften der charakteristischen Pfeilform.

Eingaberegeln

• Eine Seite (Basis a oder Seite b) erforderlich
• 2 Winkel erforderlich
• Dezimalzahlen mit Punkt oder Komma

Pfeil-Eigenschaften

• Spitzenwinkel: α = 30-90° (optimal: 45°)
• Reflexwinkel: β > 180° (einspringend)
• Navigation: Eindeutige Richtungsanzeige

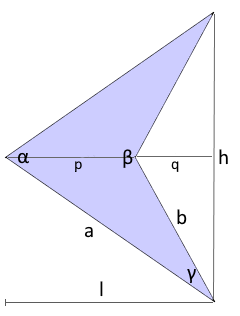
Pfeilviereck mit Bezeichnungen


Das Pfeilviereck

Ein Pfeilviereck ist eine spezielle Form des konkaven Vierecks mit charakteristischer Pfeilform. Es entsteht durch eine stark einspringende Ecke (Reflexwinkel >> 180°) und eine spitze Pfeilspitze, wodurch eine unverwechselbare Navigations- und Richtungsform entsteht.

➤ Pfeil-Eigenschaften
  • • Basis: Gerade Grundlinie (Seite a)
  • • Spitze: Spitzer Winkel α (30-60°)
  • • Reflexwinkel: β deutlich > 180°
  • • Richtung: Klare Navigation
🎯 Anwendungsbereiche
  • • Navigation: UI/UX-Interfaces
  • • Verkehr: Beschilderung & Wegweiser
  • • Design: Logos & Grafiken
  • • Technik: Strömungsrichtungen

Charakteristische Eigenschaften:

  • Basis: Gerade Linie als Grundlage des Pfeils (Seite a)
  • Pfeilspitze: Spitzer Winkel α (typisch 30-60°)
  • Stark einspringende Ecke: Reflexwinkel β deutlich > 180°
  • Außenliegende Diagonale: Eine Diagonale verläuft außerhalb
  • Eindeutige Richtung: Klare Pfeilrichtung zur Spitze


Grundlegende Formeln

➤ Pfeilviereck Formeln:

Umfang:
$$U = a + b + c + d$$
Winkelsumme:
$$\alpha + \beta + \gamma + \delta = 360°$$
Länge:
$$l = m + n$$
Höhe:
$$h = 2 \cdot \sqrt{b^2 - n^2}$$
Fläche:
$$A = \frac{l \cdot h}{2} - \frac{p \cdot h}{2}$$
Innenliegende Diagonale:
$$p = \frac{a \cdot \sin(\gamma)}{\sin\left(\frac{\beta}{2}\right)}$$
Außenliegende Diagonale:
$$q = b \cdot \sin\left(\frac{\beta}{2} - 90°\right)$$

Geometrische Konstruktion

🏗️ Konstruktions-Methoden:

Methode 1 - Basis und Spitze:
1. Zeichne die Basis a als horizontale Linie
2. Konstruiere die Pfeilspitze mit Winkel α
3. Bestimme die einspringende Ecke γ
4. Verbinde alle Punkte zum Pfeilviereck
Methode 2 - Reflexwinkel-basiert:
1. Starte mit einem konvexen Viereck
2. "Drücke" eine Ecke stark nach innen (δ > 200°)
3. Forme die gegenüberliegende Seite zur Spitze
4. Justiere die Proportionen für optimale Pfeilform

Pfeil-Parameter und Proportionen

Optimale Proportionen:
Für eine harmonische Pfeilform haben sich folgende Verhältnisse bewährt:

  • Spitzenwinkel: α = 45° ± 15° (optimal für Erkennbarkeit)
  • Reflexwinkel: β = 240° ± 30° (starke Konkavität)
  • Basis-Spitzen-Verhältnis: 2:1 bis 3:1
  • Einsprungstiefe: 20-40% der Basislänge

Anwendungen und Verwendung

💻 Navigation & UI/UX
  • • Pfeilbuttons in Software-Interfaces
  • • Navigationsmenüs und Dropdown-Indikatoren
  • • Richtungsanzeigen in Karten und Apps
  • • Spieler-Avatare und Bewegungsrichtungen
🚗 Verkehr & Beschilderung
  • • Verkehrsschilder und Wegweiser
  • • Bodenpfeile in Parkhäusern
  • • Flughäfen und Bahnhöfe
  • • Notausgang-Beschilderung

Design und Grafik:
• Logo-Design und Corporate Identity
• Infografiken und Diagramme
• Präsentationsfolien
• Webdesign-Elemente

Technische Anwendungen:
• Strömungsrichtungen in der Fluiddynamik
• Kraftvektoren in der Mechanik
• Elektronische Schaltpläne
• Architektonische Grundrisse

Mathematische Eigenschaften

Symmetrie-Eigenschaften:
• Achsensymmetrie (wenn b = c und a = d)
• Keine Punktsymmetrie (aufgrund der Pfeilrichtung)
• Keine Rotationssymmetrie

Flächenverteilung:
Bei symmetrischen Pfeilvierecken ist die Fläche typischerweise wie folgt verteilt: $$\frac{A_{\text{Spitze}}}{A_{\text{Basis}}} \approx \frac{1}{2} \text{ bis } \frac{2}{3}$$
Schwerpunkt:
Der Schwerpunkt liegt typischerweise im hinteren Drittel (näher zur Basis): $$x_S = \frac{1}{3}a \text{ bis } \frac{2}{5}a$$

Wahrnehmungspsychologie

Visuelle Wirkung:
Die Pfeilform hat starke psychologische Wirkungen:

  • Richtungsweisung: Intuitive Erfassung der Bewegungsrichtung
  • Dynamik: Vermittelt Bewegung und Vorwärtsdrang
  • Hierarchie: Führt das Auge in eine bestimmte Richtung
  • Handlungsaufforderung: "Call-to-Action" Wirkung

Kulturelle Unterschiede:
• In westlichen Kulturen: Links-nach-rechts Leserichtung
• In arabischen Kulturen: Rechts-nach-links Präferenz
• Universell: Aufwärts = positiv, abwärts = negativ

Optimale Gestaltung:
Für maximale Wirksamkeit sollten Pfeilvierecke: $$\text{Kontrastverhältnis} > 3:1 \text{ (WCAG-konform)}$$ $$\text{Mindestgröße} > 16 \text{ Pixel (Touch-Interface)}$$ $$\text{Abstand zu anderen Elementen} > 8 \text{ Pixel}$$

🌟 Pfeilviereck - Navigation & Richtung:
  • Charakteristische Form: Spitzer Winkel + starker Reflexwinkel
  • Universelle Verständlichkeit: Intuitive Richtungsanzeige
  • Vielseitige Anwendung: Von UI-Design bis Verkehrsbeschilderung
  • Psychologische Wirkung: Dynamik und Handlungsaufforderung
  • Mathematische Präzision: Optimierte Proportionen für beste Erkennbarkeit
Geometrie Rechner 2D Runde Formen
Kreis
Dreiecke
Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)
Spezielle Vierecke
Quadrat
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt
Polygone
N-Eck (Universal)
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)
Allgemeine Vierecke
Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)