Pentagon Rechner

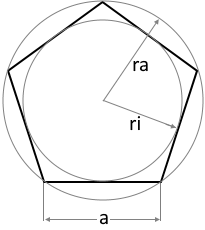
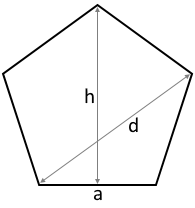
Das Pentagon (Regelmäßiges Fünfeck)

Ein Pentagon ist ein regelmäßiges Fünfeck mit fünf gleichen Seiten und fünf gleichen Innenwinkeln. Es ist eines der bekanntesten Polygone und hat faszinierende mathematische Eigenschaften, die eng mit dem Goldenen Schnitt verbunden sind.

Eigenschaften:

• Fünf gleiche Seiten: alle Seiten haben die Länge $a$
• Fünf gleiche Innenwinkel: jeder Winkel beträgt $108°$
• Fünf Symmetrieachsen: durch jede Ecke und Seitenmitte
• 5-zählige Rotationssymmetrie: alle 72° identisch
• Goldener Schnitt: Verhältnis Diagonale zu Seite = $\phi \approx 1{,}618$

Grundlegende Formeln

Alle Berechnungen basieren auf der Seitenlänge $a$:

Innenwinkel:
$$\alpha = \frac{(5-2) \times 180°}{5} = 108°$$
Diagonale:
$$d = a \times \frac{1 + \sqrt{5}}{2} = a \times \phi \approx 1{,}618 \times a$$
Fläche:
$$A = \frac{\sqrt{25 + 10\sqrt{5}}}{4} \times a^2 \approx 1{,}720 \times a^2$$
Umfang:
$$U = 5 \times a$$
Inkreisradius:
$$r = \frac{a}{2 \tan(36°)} \approx 0{,}688 \times a$$
Umkreisradius:
$$R = \frac{a}{2 \sin(36°)} \approx 0{,}851 \times a$$

Der Goldene Schnitt im Pentagon

Das Pentagon ist eng mit dem Goldenen Schnitt $\phi = \frac{1 + \sqrt{5}}{2} \approx 1{,}618$ verbunden:

Diagonalenverhältnis:
$$\frac{d}{a} = \phi = \frac{1 + \sqrt{5}}{2}$$
Pentagramm:
Verbindet man alle Ecken mit Diagonalen, entsteht ein Pentagramm (5-zackiger Stern), in dem ebenfalls überall der Goldene Schnitt auftritt.

Fibonacci-Beziehung:
$$\phi = \lim_{n \to \infty} \frac{F_{n+1}}{F_n}$$ (Fibonacci-Verhältnis)

Rückrechnungsformeln

Seitenlänge aus anderen Werten:
• Aus Diagonale: $$a = \frac{d}{\phi} = d \times (\phi - 1) \approx 0{,}618 \times d$$ • Aus Fläche: $$a = \sqrt{\frac{4A}{\sqrt{25 + 10\sqrt{5}}}} \approx 0{,}763 \times \sqrt{A}$$ • Aus Umfang: $$a = \frac{U}{5}$$ • Aus Inkreisradius: $$a = 2r \tan(36°) \approx 1{,}453 \times r$$ • Aus Umkreisradius: $$a = 2R \sin(36°) \approx 1{,}176 \times R$$

Konstruktion des Pentagons

Klassische Konstruktion mit Zirkel und Lineal:

1. Zeichne einen Kreis mit Mittelpunkt O
2. Zeichne zwei senkrechte Durchmesser
3. Halbiere den Radius und konstruiere den Goldenen Schnitt
4. Bestimme die Pentagon-Eckpunkte auf dem Kreis
5. Verbinde die Eckpunkte zu einem regelmäßigen Fünfeck

Näherungskonstruktion:
Teile den Umkreis in 5 gleiche Teile (je 72°) und verbinde die Punkte.

Beispielrechnung

Gegeben: Seitenlänge $a = 5$ cm

Diagonale berechnen:
$d = a \times \phi = 5 \times 1{,}618 \approx 8{,}09$ cm

Fläche berechnen:
$A = 1{,}720 \times a^2 = 1{,}720 \times 25 = 43{,}01$ cm²

Umfang berechnen:
$U = 5 \times a = 5 \times 5 = 25$ cm

Inkreisradius berechnen:
$r = 0{,}688 \times a = 0{,}688 \times 5 \approx 3{,}44$ cm

Umkreisradius berechnen:
$R = 0{,}851 \times a = 0{,}851 \times 5 \approx 4{,}25$ cm

Praktische Anwendungen

Pentagone finden sich in vielen Bereichen:

• Architektur: Pentagon-Gebäude, Festungsanlagen
• Natur: Blüten (Apfel, Kirsche), Seesterne, Quallen
• Kristallographie: Ikosaeder, Dodekaeder
• Design: Logos, Embleme, Münzen
• Militär: Das Pentagon in Washington D.C.
• Spiele: Brettspiele, Puzzles

Mathematische Besonderheiten

Unmöglichkeit regelmäßiger Parkettierung:
Regelmäßige Pentagone können die Ebene nicht vollständig und lückenlos parkettieren, da $108°$ kein Teiler von $360°$ ist.

Platonische Körper:
Das Pentagon bildet die Seitenflächen des Dodekaeders (einer der fünf platonischen Körper).

Pentagramm:
Das in das Pentagon eingeschriebene Pentagramm (5-zackiger Stern) zeigt an allen Schnittpunkten das Verhältnis des Goldenen Schnitts.

Verwandte Polygone

Andere regelmäßige Polygone:
• Dreieck (3 Seiten): $\alpha = 60°$
• Quadrat (4 Seiten): $\alpha = 90°$
• Pentagon (5 Seiten): $\alpha = 108°$
• Hexagon (6 Seiten): $\alpha = 120°$
• Octagon (8 Seiten): $\alpha = 135°$

Allgemeine Formel für n-Ecke:
$$\alpha = \frac{(n-2) \times 180°}{n}$$

Historisches und Kulturelles

Antike Mathematik:
Die Griechen entdeckten die Verbindung zwischen Pentagon und Goldenem Schnitt. Die Pythagoreer verwendeten das Pentagramm als Erkennungszeichen.

Symbolik:
• Symbol für Harmonie und Vollkommenheit
• In vielen Kulturen als heilige Zahl 5 verehrt
• Pentagramm in Magie und Mystik
• Staatssymbole und Flaggen (USA, China, etc.)

Geometrie Rechner 2D Runde Formen

Kreis

Dreiecke

Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)

Spezielle Vierecke

Quadrat
Rechteck
Parallelogramm
Raute
Trapez
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rechteckiger Rahmen
Konkaves Viereck Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt

Polygone

Pentagon (Fünfeck)
Hexagon (Sechseck)
Heptagon (Siebeneck)

Allgemeine Vierecke

Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)