Konkaves Viereck Rechner

Online Rechner für einspringende Vierecke mit Reflexwinkeln


🔀 Konkaves Viereck Rechner

Einspringende Vierecke mit Reflexwinkeln > 180°

Einheiten
Einheiten
Einheiten
°
°
🔀
Konkaves Viereck: Ein Winkel α > 180° (Reflexwinkel) + Winkelsumme = 360°
⚠️ Fehler:

Geben Sie drei Seitenlängen und zwei Winkel ein. Der Rechner berechnet alle anderen Eigenschaften des konkaven Vierecks.

Eingaberegeln

• Drei Seiten (a, b, c) sind erforderlich
• 2 Winkel sind erforderlich
• Dezimalzahlen mit Punkt oder Komma

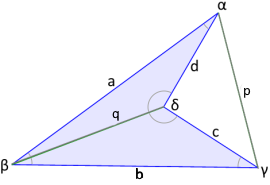
Konkaves Viereck mit Bezeichnungen

Konkave Eigenschaften

• Reflexwinkel: Ein Winkel > 180°
• Einspringend: Charakteristische "eingebeulte" Form
• Triangulation: Spezielle Flächenberechnung


Das konkave Viereck

Ein konkaves Viereck (auch einspringendes Viereck genannt) ist ein Viereck mit mindestens einem Reflexwinkel (Innenwinkel > 180°). Diese besondere Form entsteht, wenn eine Ecke nach "innen" einspringt, wodurch das Viereck eine charakteristische "eingebeulte" Form erhält.

🔀 Konkave Eigenschaften
  • • Reflexwinkel: Ein Innenwinkel > 180°
  • • Nicht konvex: Einspringende Form
  • • Winkelsumme: α + β + γ + δ = 360°
  • • Spezielle Diagonalen: Teilweise außerhalb
📐 Berechnungsarten
  • • Triangulation: Zerlegung in Dreiecke
  • • Cosinussatz: Für Diagonalen
  • • Heron-Formel: Für Teilflächen
  • • Vorzeichen-Kontrolle: Orientierung beachten

Eigenschaften:

  • Mindestens ein Reflexwinkel: Ein Innenwinkel α > 180°
  • Nicht konvex: Die Verbindungslinie zweier Punkte kann außerhalb des Vierecks liegen
  • Winkelsumme: $\alpha + \beta + \gamma + \delta = 360°$ (wie bei allen Vierecken)
  • Diagonalen: Mindestens eine Diagonale liegt außerhalb des Vierecks
  • Spezielle Flächenberechnung: Erfordert Zerlegung oder Vorzeichen-Beachtung


Grundlegende Formeln

📐 Konkave Viereck Formeln:

Diagonale p
$$p =\sqrt{a^2+b^2-2 \cdot a \cdot b \cdot \cos(\beta)}$$
Diagonale q
$$q =\sqrt{b^2+c^2-2 \cdot b \cdot c \cdot \cos(\gamma)}$$
Seitenlänge d
$$d=\sqrt{a^2+q^2-2 \cdot a \cdot q \cdot \cos(\beta_1)}$$ $$\beta_1 =\beta- \arccos\left(\frac{b^2+q^2-c^2}{2 \cdot b \cdot q}\right)$$ Winkel α (Reflexwinkel)
$$\alpha=\arccos\left(\frac{a^2+d^2-q^2}{2 \cdot a \cdot d}\right)$$
Winkel δ
$$\delta=360°-\alpha-\beta-\gamma$$
Umfang U
$$U=a+b+c+d$$
Flächeninhalt A
$$A=\sqrt{s \cdot (s-a) \cdot (s-d) \cdot (s-q)} + \sqrt{t \cdot (t-b) \cdot (t-c) \cdot (t-q)}$$ wo $s=\frac{a+d+q}{2}$ und $t=\frac{b+c+q}{2}$

Winkelsumme (unverändert):
$$\alpha + \beta + \gamma + \delta = 360°$$
Modifizierte Bretschneider-Formel:
$$A = \sqrt{(s-a)(s-b)(s-c)(s-d) - abcd \cdot \cos^2\left(\frac{\alpha+\gamma}{2}\right)}$$ wobei $s = \frac{a+b+c+d}{2}$ und der Cosinus-Term das Vorzeichen berücksichtigt.
Triangulation (empfohlene Methode):
$$A = |A_{\triangle 1}| + |A_{\triangle 2}|$$ mit Vorzeichen-korrekter Addition der Teilflächen.

Reflexwinkel und ihre Eigenschaften

Definition Reflexwinkel:
Ein Reflexwinkel ist ein Winkel α mit $180° < \alpha < 360°$. Bei konkaven Vierecken liegt mindestens ein solcher Winkel vor.

Erkennung konkaver Vierecke:
• Mindestens ein Innenwinkel > 180°
• Eine Diagonale liegt außerhalb des Vierecks
• Nicht alle Punkte liegen auf derselben Seite einer Geraden durch zwei benachbarte Eckpunkte

Konsequenzen für Berechnungen:
• Standard-Flächenformeln können negative Werte liefern
• Triangulation mit Vorzeichen-Kontrolle erforderlich
• Diagonalen-Schnittpunkt kann außerhalb des Vierecks liegen

Flächenberechnung bei konkaven Vierecken

🔄 Flächenberechnungs-Methoden:

Methode 1 - Triangulation:
Das Viereck wird durch eine Diagonale in zwei Dreiecke zerlegt:
  • Wähle eine Diagonale, die innerhalb des Vierecks liegt
  • Berechne die Flächen beider Dreiecke mit der Heron-Formel
  • Addiere die Flächen (beide positiv)
Methode 2 - Shoelace-Formel (Koordinaten):
$$A = \frac{1}{2}|x_1(y_2-y_4) + x_2(y_3-y_1) + x_3(y_4-y_2) + x_4(y_1-y_3)|$$ Diese Formel berücksichtigt automatisch die Orientierung.

Methode 3 - Zerlegung in konvexe Teile:
• Zerlege das konkave Viereck in konvexe Polygone
• Berechne die Flächen der konvexen Teile
• Addiere alle Teilflächen

Beispielrechnung

📝 Beispiel mit a = 6 cm, b = 4 cm, c = 8 cm, d = 5 cm, α = 200°:

Umfang berechnen:
$U = a + b + c + d = 6 + 4 + 8 + 5 = 23$ cm

Weitere Winkel berechnen:
Da $\alpha = 200°$ ein Reflexwinkel ist, müssen die anderen Winkel entsprechend kleiner sein:
$\beta + \gamma + \delta = 360° - 200° = 160°$

Triangulation für Fläche:
Wähle Diagonale $p$ zwischen den Eckpunkten ohne Reflexwinkel:
Dreieck 1: Seiten $a = 6$, $b = 4$, $p$ (zu berechnen)
Dreieck 2: Seiten $c = 8$, $d = 5$, $p$ (zu berechnen)

Validierung:
Bei einem Reflexwinkel von 200° muss das Viereck konkav sein ✓

Diagonalen in konkaven Vierecken

Besonderheiten der Diagonalen:
• Mindestens eine Diagonale liegt teilweise außerhalb des Vierecks
• Der Schnittpunkt der Diagonalen kann außerhalb liegen
• Nicht alle Diagonalen-Eigenschaften konvexer Vierecke gelten

Berechnung der Diagonalen:
Mit dem Cosinussatz für die Dreiecke, die durch die Diagonalen entstehen: $$p^2 = a^2 + b^2 - 2ab\cos(\beta)$$ Dabei ist $\beta$ der Winkel zwischen den Seiten $a$ und $b$.

Wahl der richtigen Diagonale:
Für Flächenberechnungen sollte die Diagonale gewählt werden, die:
• Vollständig innerhalb des Vierecks liegt
• Das Viereck in zwei "einfache" Dreiecke teilt
• Keine zusätzlichen Komplikationen verursacht

Klassifikation konkaver Vierecke

Nach Anzahl der Reflexwinkel:

  • Einfach konkav: Genau ein Reflexwinkel
  • Mehrfach konkav: Mehrere Reflexwinkel (selten bei Vierecken)

Nach Form des Einsprungs:
  • Schwach konkav: Reflexwinkel nahe 180°
  • Stark konkav: Reflexwinkel deutlich > 180°
  • Extrem konkav: Reflexwinkel nahe 360° (fast "umgeklappt")

Spezielle Formen:
  • Pfeilform: Eine Ecke springt stark ein
  • L-Form: Rechtwinkliger Einsprung
  • Bumerang-Form: Geschwungener Einsprung

Konstruktion konkaver Vierecke

Methode 1 - Aus konvexem Viereck:
1. Beginne mit einem konvexen Viereck
2. "Drücke" eine Ecke nach innen
3. Der Winkel an dieser Ecke wird zum Reflexwinkel
4. Passe die Seitenlängen entsprechend an

Methode 2 - Koordinaten-basiert:
1. Setze drei Eckpunkte im Uhrzeigersinn
2. Platziere den vierten Punkt so, dass er einen Einsprung erzeugt
3. Prüfe, ob der entstehende Winkel > 180° ist

Methode 3 - Winkel-basiert:
1. Bestimme einen Reflexwinkel > 180°
2. Verteile die restlichen 160° - 180° auf die anderen Winkel
3. Konstruiere das Viereck schrittweise

Praktische Anwendungen

🏗️ Architektur & Design
  • • Atriumhäuser mit einspringenden Ecken
  • • Moderne Gebäudeformen mit Nischen
  • • Innenhöfe und Lichtschächte
  • • Dachformen mit Einschnitten
⚙️ Technische Anwendungen
  • • Maschinenbauteile mit Aussparungen
  • • Stanzteile und Blechformen
  • • Elektronik-Gehäuse mit Einbuchtungen
  • • Verpackungsdesign

Computergrafik:
• Polygon-Clipping und -Triangulation
• 2D-Spiele mit komplexen Formen
• CAD-Systeme für unregelmäßige Formen
• Mesh-Generierung für konkave Bereiche

Mathematische Herausforderungen

Numerische Probleme:
• Flächenberechnung kann instabil werden
• Rundungsfehler bei sehr spitzen Einsprüngen
• Orientierungs-abhängige Berechnungen

Algorithmus-Design:
• Automatische Erkennung der Konkavität
• Wahl der optimalen Triangulation
• Robuste Implementierung der Formeln

Lösungsansätze:
• Verwendung höherer Präzision
• Multiple Berechnungsverfahren zur Kontrolle
• Spezielle Behandlung von Grenzfällen
• Grafische Validierung der Ergebnisse

Validierung und Plausibilitätsprüfung

Konsistenz-Checks:
• Winkelsumme muss exakt 360° betragen
• Mindestens ein Winkel > 180°
• Fläche muss positiv sein
• Umfang muss größer als längste Diagonale sein

Geometrische Validierung:
• Dreiecks-Ungleichung für alle Teilstücke
• Diagonalen müssen realisierbar sein
• Keine Selbstüberschneidungen
• Orientierung der Eckpunkte prüfen

Häufige Fehlerquellen:
• Falsche Vorzeichen bei Flächenberechnung
• Verwechslung von Innen- und Außenwinkeln
• Fehlerhafte Triangulation
• Ignorieren der Konkavität bei Standard-Formeln

Erweiterte Eigenschaften

Schwerpunkt konkaver Vierecke:
Der Schwerpunkt liegt nicht unbedingt innerhalb des Vierecks und muss durch gewichtete Mittelung der Teilbereiche berechnet werden.

Umkreis und Inkreis:
• Umkreis existiert nur in speziellen Fällen
• Inkreis ist bei konkaven Vierecken nicht definiert
• Ersatzkreise können für bestimmte Anwendungen konstruiert werden

Symmetrie-Eigenschaften:
• Achsensymmetrie möglich, aber selten
• Punktsymmetrie praktisch ausgeschlossen
• Drehsymmetrie nur in sehr speziellen Fällen

Transformation und Skalierung:
• Affine Transformationen erhalten Konkavität
• Skalierung verändert Winkel nicht
• Rotation kann die "Richtung" der Konkavität ändern

🌟 Konkaves Viereck - Einspringende Geometrie:
  • Reflexwinkel: Charakteristischer Winkel > 180° für einspringende Form
  • Spezielle Mathematik: Triangulation und Vorzeichen-bewusste Berechnung
  • Praktische Relevanz: Architektur, Maschinenbau und Design
  • Geometrische Komplexität: Erweiterte Berechnungsmethoden erforderlich
  • Anwendungsvielfalt: Von Gebäuden bis zu technischen Bauteilen
Geometrie Rechner 2D Runde Formen
Kreis
Dreiecke
Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)
Spezielle Vierecke
Quadrat
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt
Polygone
N-Eck (Universal)
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)
Allgemeine Vierecke
Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)