Gleichschenkliges Dreieck Rechner

Online Rechner für alle Berechnungen am gleichschenkligen Dreieck


🔺 Gleichschenkliges Dreieck Rechner

Symmetrische Dreiecke mit zwei gleichen Schenkeln

Einheiten
Einheiten
Einheiten
°
°
Dreiecksfläche
💡 Symmetrisch: Zwei gleiche Schenkel mit Spiegelachse durch die Höhe
⚠️ Fehler:

Geben Sie mindestens zwei bekannte Werte ein. Der Rechner berechnet automatisch alle anderen Eigenschaften des gleichschenkligen Dreiecks.

Eingaberegeln

• Mindestens zwei Werte erforderlich
• Winkel in Grad eingeben
• Dezimalzahlen mit Punkt oder Komma
• Schenkel sind die beiden gleichen Seiten

Dreieck-Eigenschaften

• Symmetrie: Spiegelachse durch Höhe zur Basis
• Gleiche Schenkel: a = a
• Gleiche Basiswinkel: α = α

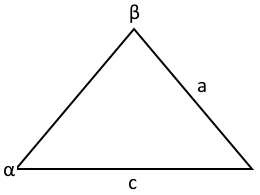
gleichseitiges Dreieck


Das gleichschenklige Dreieck

Ein gleichschenkliges Dreieck ist ein Dreieck mit zwei gleich langen Seiten, den sogenannten Schenkeln. Die dritte Seite wird als Basis bezeichnet. Es hat eine Symmetrieachse, die durch die Spitze und die Mitte der Basis verläuft.

🔺 Dreiecks-Eigenschaften
  • • Zwei gleiche Seiten: Schenkel a = a
  • • Zwei gleiche Winkel: Basiswinkel α = α
  • • Symmetrieachse: Von Spitze zur Basismitte
  • • Höhe zur Basis: Teilt Basis in zwei gleiche Hälften
📐 Berechnungsgrundlagen
  • • Winkelsumme: 2α + β = 180°
  • • Höhe: h = √(a² - (c/2)²)
  • • Fläche: A = ½ × c × h
  • • Umfang: U = 2a + c

Eigenschaften:

  • Zwei gleiche Seiten: Die Schenkel $a$ sind gleich lang
  • Zwei gleiche Winkel: Die Basiswinkel $\alpha$ sind gleich groß
  • Eine Symmetrieachse: Von der Spitze zur Basismitte
  • Höhe zur Basis: Teilt die Basis in zwei gleiche Hälften


Formeln für das gleichschenklige Dreieck

🔺 Gleichschenkliges Dreieck Formeln:

Bezeichnungen: $a$ = Schenkel, $c$ = Basis, $h$ = Höhe zur Basis, $\alpha$ = Basiswinkel, $\beta$ = Spitzenwinkel

Winkelsumme:
$$\alpha + \alpha + \beta = 180° \quad \text{bzw.} \quad 2\alpha + \beta = 180°$$
Höhe zur Basis (Pythagoras):
$$h = \sqrt{a^2 - \left(\frac{c}{2}\right)^2}$$
Fläche:
$$A = \frac{c \cdot h}{2}$$
Umfang:
$$U = 2a + c$$
Trigonometrische Beziehungen:
$$\sin \alpha = \frac{h}{a} \quad \text{und} \quad \cos \alpha = \frac{c/2}{a}$$

Beispielrechnung

📝 Beispiel mit Schenkel a = 5 cm, Basis c = 6 cm:

Höhe berechnen (Pythagoras):
$h = \sqrt{a^2 - (c/2)^2} = \sqrt{5^2 - 3^2} = \sqrt{25 - 9} = \sqrt{16} = 4$ cm

Fläche berechnen:
$A = \frac{c \times h}{2} = \frac{6 \times 4}{2} = 12$ cm²

Umfang berechnen:
$U = 2a + c = 2 \times 5 + 6 = 16$ cm

Basiswinkel berechnen:
$\cos \alpha = \frac{c/2}{a} = \frac{3}{5} = 0{,}6$
$\alpha = \arccos(0{,}6) \approx 53{,}13°$

Spitzenwinkel berechnen:
$\beta = 180° - 2\alpha = 180° - 2 \times 53{,}13° \approx 73{,}74°$

Rückrechnungsformeln

🔄 Umkehrformeln:

Schenkel aus anderen Werten:
• Aus Basis und Höhe: $a = \sqrt{(c/2)^2 + h^2}$
• Aus Basis und Basiswinkel: $a = \frac{c/2}{\cos(\alpha)}$
• Aus Höhe und Basiswinkel: $a = \frac{h}{\sin(\alpha)}$
Basis aus anderen Werten:
• Aus Schenkel und Höhe: $c = 2\sqrt{a^2 - h^2}$
• Aus Schenkel und Basiswinkel: $c = 2a \times \cos(\alpha)$
• Aus Fläche und Höhe: $c = \frac{2A}{h}$

Besondere Fälle

Entartete Fälle:

  • $c = 0$: Das Dreieck wird zu einer Linie (entartet)
  • $c = 2a$: Das Dreieck wird zu einer Linie (gestreckt)
  • $a = b = c$: Übergang zum gleichseitigen Dreieck
Spezielle Winkel:
  • $\alpha = 60°$: Gleichseitiges Dreieck ($\beta = 60°$)
  • $\alpha = 45°$: Rechtwinklig-gleichschenkliges Dreieck ($\beta = 90°$)
  • $\alpha = 30°$: Sehr spitzes gleichschenkliges Dreieck ($\beta = 120°$)

Praktische Anwendungen

🏗️ Architektur & Bau
  • • Giebeldächer und Dachstühle
  • • Türme und Brückenkonstruktionen
  • • Verstrebungen und Fachwerke
  • • Spitzbogenarchitektur
🔬 Technik & Wissenschaft
  • • Navigation und Vermessung
  • • Optische Geräte und Prismen
  • • Kristallformen in der Natur
  • • Design und symmetrische Muster

Gleichschenklige Dreiecke kommen häufig vor:

  • Architektur: Giebeldächer, Türme, Brücken
  • Technik: Verstrebungen, Fachwerke
  • Natur: Blattformen, Kristalle
  • Navigation: Peilungen, Vermessung
  • Design: Logos, symmetrische Muster

🌟 Gleichschenkliges Dreieck - Symmetrische Eleganz:
  • Symmetrie: Spiegelachse durch Spitze und Basismitte
  • Gleiche Schenkel: Zwei identische Seitenlängen
  • Gleiche Basiswinkel: Perfekte Symmetrie der Winkel
  • Praktische Relevanz: Von Architektur bis Navigation
  • Mathematische Eleganz: Einfache und klare Formeln
Geometrie Rechner 2D Runde Formen
Kreis
Dreiecke
Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)
Spezielle Vierecke
Quadrat
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt
Polygone
N-Eck (Universal)
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)
Allgemeine Vierecke
Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)