Parallelogramm Rechner

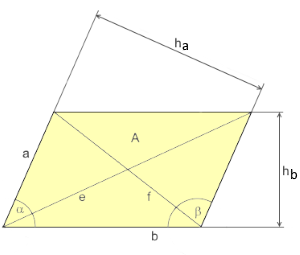
Das Parallelogramm

Ein Parallelogramm ist ein Viereck, bei dem jeweils die gegenüberliegenden Seiten parallel und gleich lang sind. Es ist eine der grundlegenden Formen der ebenen Geometrie und bildet die Basis für viele andere geometrische Figuren.

Eigenschaften:

• Gegenüberliegende Seiten: parallel und gleich lang
• Gegenüberliegende Winkel: gleich groß
• Benachbarte Winkel: ergänzen sich zu 180° (supplementär)
• Diagonalen: halbieren sich gegenseitig
• Symmetrie: punktsymmetrisch zum Schnittpunkt der Diagonalen

Grundlegende Formeln

Fläche:
$$A = a \cdot h_a = b \cdot h_b = a \cdot b \cdot \sin(\alpha)$$
Umfang:
$$U = 2(a + b)$$
Höhen:
$$h_a = \frac{A}{a} = b \cdot \sin(\alpha)$$ $$h_b = \frac{A}{b} = a \cdot \sin(\alpha)$$
Diagonalen (Parallelogramm-Gesetz):
$$e^2 = a^2 + b^2 + 2ab\cos(\alpha)$$ $$f^2 = a^2 + b^2 - 2ab\cos(\alpha)$$
Beziehung zwischen den Diagonalen:
$$e^2 + f^2 = 2(a^2 + b^2)$$

Winkelbeziehungen

Grundlegende Beziehungen:
• $\alpha + \beta = 180°$ (benachbarte Winkel)
• Gegenüberliegende Winkel sind gleich
• $\gamma = \alpha$ und $\delta = \beta$

Spezialfall Rhombus:
Wenn $a = b$, wird das Parallelogramm zum Rhombus.

Spezialfall Rechteck:
Wenn $\alpha = \beta = 90°$, wird das Parallelogramm zum Rechteck.

Beispielrechnung

Gegeben: Seite $a = 8$ cm, Seite $b = 6$ cm, Winkel $\alpha = 60°$

Fläche berechnen:
$A = a \cdot b \cdot \sin(\alpha) = 8 \cdot 6 \cdot \sin(60°) = 48 \cdot 0{,}866 \approx 41{,}57$ cm²

Umfang berechnen:
$U = 2(a + b) = 2(8 + 6) = 28$ cm

Höhen berechnen:
$h_a = b \cdot \sin(\alpha) = 6 \cdot \sin(60°) \approx 5{,}20$ cm
$h_b = a \cdot \sin(\alpha) = 8 \cdot \sin(60°) \approx 6{,}93$ cm

Diagonalen berechnen:
$e = \sqrt{a^2 + b^2 + 2ab\cos(\alpha)} = \sqrt{64 + 36 + 96 \cdot 0{,}5} = \sqrt{148} \approx 12{,}17$ cm
$f = \sqrt{a^2 + b^2 - 2ab\cos(\alpha)} = \sqrt{64 + 36 - 48} = \sqrt{52} \approx 7{,}21$ cm

Konstruktion eines Parallelogramms

Methode 1 - Zwei Seiten und ein Winkel:
1. Zeichne die Seite $a$
2. Trage an einem Ende den Winkel $\alpha$ an
3. Zeichne die Seite $b$ im Winkel $\alpha$
4. Vervollständige durch parallele Linien

Methode 2 - Zwei Seiten und eine Höhe:
1. Zeichne die Grundseite $a$
2. Errichte die Höhe $h_a$ senkrecht dazu
3. Zeichne parallel zur Grundseite in Höhe $h_a$
4. Vervollständige mit der Seite $b$

Methode 3 - Zwei Diagonalen:
1. Zeichne die beiden Diagonalen sich halbierend
2. Verbinde die Eckpunkte zum Parallelogramm

Spezielle Parallelogramme

Rechteck:
• Alle Winkel sind 90°
• Diagonalen sind gleich lang: $e = f = \sqrt{a^2 + b^2}$
• Fläche: $A = a \cdot b$

Rhombus (Raute):
• Alle Seiten sind gleich lang: $a = b$
• Diagonalen stehen senkrecht aufeinander
• Fläche: $A = a^2 \cdot \sin(\alpha) = \frac{e \cdot f}{2}$

Quadrat:
• Spezialfall: Rechteck UND Rhombus
• $a = b$ und $\alpha = 90°$
• Diagonalen: gleich lang und senkrecht
• Fläche: $A = a^2$

Flächenberechnungen

Verschiedene Methoden:
1. Grundseite × Höhe: $A = a \cdot h_a = b \cdot h_b$
2. Zwei Seiten und Winkel: $A = a \cdot b \cdot \sin(\alpha)$
3. Kreuzprodukt der Diagonalen: $A = \frac{e \cdot f \cdot \sin(\gamma)}{2}$ (γ = Winkel zwischen Diagonalen)
4. Vektorprodukt: $A = |\vec{a} \times \vec{b}|$ (bei Vektordarstellung)

Besonderheit:
Die Fläche bleibt konstant bei Scherung (Parallelverschiebung einer Seite parallel zur gegenüberliegenden Seite).

Praktische Anwendungen

Technik und Konstruktion:
• Parallelführungen in Maschinen
• Kräfteparallelogramm in der Statik
• Gelenkparallelogramm in der Mechanik
• Pantograph (Storchschnabel) zum maßstäblichen Kopieren

Architektur und Design:
• Grundrisse von Gebäuden
• Fliesenmuster und Parkettierungen
• Fachwerkkonstruktionen
• Moderne Architektur (schiefe Gebäude)

Mathematik und Physik:
• Vektoraddition (Parallelogramm-Regel)
• Koordinatensysteme (schiefwinklig)
• Kristallgitter in der Festkörperphysik
• Transformationen in der linearen Algebra

Parallelogramm-Gesetz der Diagonalen

Das Parallelogramm-Gesetz ist eine wichtige Beziehung: $$e^2 + f^2 = 2(a^2 + b^2)$$
Bedeutung:
• Die Summe der Quadrate der Diagonalen entspricht der doppelten Summe der Quadrate der Seiten
• Gilt nur für Parallelogramme (Erkennungsmerkmal)
• Wichtig in der Vektorrechnung und Funktionalanalysis

Umkehrung:
Wenn für ein Viereck $e^2 + f^2 = 2(a^2 + b^2)$ gilt, dann ist es ein Parallelogramm.

Vektorielle Darstellung

Seiten als Vektoren:
Sei $\vec{a}$ und $\vec{b}$ die beiden Seitenvektoren:
• Diagonalvektoren: $\vec{e} = \vec{a} + \vec{b}$ und $\vec{f} = \vec{a} - \vec{b}$
• Fläche: $A = |\vec{a} \times \vec{b}| = |\vec{a}| \cdot |\vec{b}| \cdot \sin(\alpha)$
• Skalarprodukt: $\vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot \cos(\alpha)$

Koordinaten:
Bei Koordinaten A(0,0), B(a,0), C(a+p,q), D(p,q):
• Fläche: $A = |a \cdot q|$
• Diagonalen: $e = \sqrt{(a+p)^2 + q^2}$, $f = \sqrt{(a-p)^2 + q^2}$

Transformationen und Affine Geometrie

Affine Transformationen:
• Parallelogramme bleiben bei affinen Transformationen erhalten
• Das Verhältnis von Flächen bleibt konstant
• Parallelität bleibt erhalten

Scherung:
• Verschiebung einer Seite parallel zur gegenüberliegenden
• Fläche bleibt konstant
• Umfang verändert sich
• Winkel verändern sich

Anwendung in der Computergrafik:
• Textur-Mapping
• 2D-Transformationen
• Skalierung und Rotation

Verwandte Sätze und Theoreme

Varignon'scher Satz:
Die Mittelpunkte der Seiten eines beliebigen Vierecks bilden ein Parallelogramm.

Apollonius-Theorem:
Für ein Parallelogramm mit Diagonalen e und f gilt:
$e^2 + f^2 = 2(a^2 + b^2)$

Schwerpunkt:
Der Schwerpunkt liegt im Schnittpunkt der Diagonalen und teilt jede Diagonale im Verhältnis 1:1.

Flächenteilung:
Jede durch den Mittelpunkt gehende Gerade teilt das Parallelogramm in zwei flächengleiche Teile.

Berechnungstipps und häufige Fehler

Häufige Fehlerquellen:
• Verwechslung von Höhe und Seitenlänge
• Falsche Winkeleinheit (Grad vs. Radiant)
• Vertauschung der Diagonalformeln
• Vergessen, dass benachbarte Winkel supplementär sind

Kontrollmöglichkeiten:
• Parallelogramm-Gesetz für Diagonalen überprüfen
• Winkel müssen sich zu 360° addieren
• Fläche über verschiedene Methoden berechnen
• Plausibilitätsprüfung der Höhen

Besondere Fälle beachten:
• Bei sehr spitzen Winkeln können numerische Probleme auftreten
• Bei α = 90° wird es zum Rechteck
• Bei a = b wird es zum Rhombus

Geometrie Rechner 2D Runde Formen

Kreis

Dreiecke

Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)

Spezielle Vierecke

Quadrat
Rechteck
Parallelogramm
Raute
Trapez
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rechteckiger Rahmen
Konkaves Viereck Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt

Polygone

Pentagon (Fünfeck)
Hexagon (Sechseck)
Heptagon (Siebeneck)

Allgemeine Vierecke

Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)