Rechteck in Quadrat umrechnen

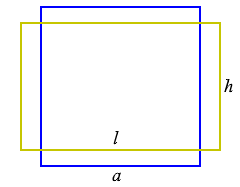
Rechteck in Quadrat umrechnen

Diese Umrechnung findet das flächengleiche Quadrat zu einem gegebenen Rechteck. Das bedeutet, dass das berechnete Quadrat exakt dieselbe Fläche hat wie das ursprüngliche Rechteck, aber als regelmäßige Form mit vier gleichen Seiten.

Anwendungsbereiche:

• Bauwesen: Umrechnung von rechteckigen in quadratische Grundflächen
• Landwirtschaft: Flächenumwandlung für optimale Feldaufteilung
• Design: Formatumwandlung bei gleichbleibender Fläche
• Mathematik: Geometrische Äquivalenzen verstehen
• Gartenbau: Umgestaltung von Beeten und Rasenflächen

Grundlegende Formel

Die zentrale Formel für die Umrechnung basiert auf der Flächengleichheit:

Rechteckfläche = Quadratfläche:
$$A_R = A_Q$$ $$a \times b = s^2$$
Quadrat-Seitenlänge:
$$s = \sqrt{a \times b}$$
Dabei ist:

• $a$ = Länge des Rechtecks
• $b$ = Breite des Rechtecks
• $s$ = Seitenlänge des flächengleichen Quadrats
• $A_R$ = Fläche des Rechtecks
• $A_Q$ = Fläche des Quadrats

Alle Berechnungsformeln

Wenn Länge und Breite gegeben sind:
• Rechteck-Fläche: $A_R = a \times b$
• Quadrat-Seitenlänge: $s = \sqrt{a \times b}$
• Quadrat-Fläche: $A_Q = s^2 = a \times b$ (Kontrolle)
• Quadrat-Umfang: $U_Q = 4s = 4\sqrt{a \times b}$
• Quadrat-Diagonale: $d_Q = s\sqrt{2} = \sqrt{2ab}$

Wenn nur die Fläche gegeben ist:
• Quadrat-Seitenlänge: $s = \sqrt{A}$
• Quadrat-Umfang: $U_Q = 4\sqrt{A}$
• Quadrat-Diagonale: $d_Q = \sqrt{2A}$

Rückrechnung vom Quadrat:
• Aus Quadrat-Seitenlänge: $A = s^2$
• Aus Quadrat-Umfang: $A = \left(\frac{U}{4}\right)^2$
• Aus Quadrat-Diagonale: $A = \frac{d^2}{2}$

Beispielrechnung

Gegeben: Rechteck mit Länge $a = 8$ m und Breite $b = 2$ m

Rechteck-Fläche berechnen:
$A_R = a \times b = 8 \times 2 = 16$ m²

Quadrat-Seitenlänge berechnen:
$s = \sqrt{a \times b} = \sqrt{8 \times 2} = \sqrt{16} = 4$ m

Verifikation - Quadrat-Fläche:
$A_Q = s^2 = 4^2 = 16$ m² ✓ (gleiche Fläche)

Weitere Quadrat-Eigenschaften:
Umfang: $U_Q = 4s = 4 \times 4 = 16$ m
Diagonale: $d_Q = s\sqrt{2} = 4 \times 1{,}414 \approx 5{,}66$ m

Geometrische Interpretation

Flächenerhaltung:
Die Umrechnung erhält die Fläche, verändert aber die Form grundlegend:

• Rechteck: Kann sehr langgestreckt oder fast quadratisch sein
• Quadrat: Immer perfekt symmetrisch mit optimalem Flächen-zu-Umfang-Verhältnis
• Umfang: Das Quadrat hat bei gleicher Fläche meist einen kleineren Umfang
• Kompaktheit: Das Quadrat ist die kompakteste rechteckige Form

Mathematisches Prinzip:
Das geometrische Mittel der Rechteckseiten ergibt die Quadratseite: $$s = \sqrt{a \times b} = \sqrt[2]{ab}$$

Umfang-Vergleich

Umfang des Rechtecks:
$$U_R = 2(a + b)$$
Umfang des flächengleichen Quadrats:
$$U_Q = 4\sqrt{ab}$$
Verhältnis der Umfänge:
$$\frac{U_Q}{U_R} = \frac{4\sqrt{ab}}{2(a + b)} = \frac{2\sqrt{ab}}{a + b}$$
Wichtige Eigenschaft: Das Quadrat hat immer den kleineren oder gleichen Umfang:
$$U_Q \leq U_R$$
Gleichheit gilt nur wenn $a = b$ (das Rechteck bereits ein Quadrat ist).

Spezialfälle und Grenzwerte

Quadratisches Rechteck ($a = b$):
• Quadrat-Seitenlänge: $s = \sqrt{a \times a} = a$
• Das "umgerechnete" Quadrat ist identisch mit dem Original

Sehr schmales Rechteck ($b \to 0$):
• Quadrat-Seitenlänge: $s \to 0$
• Fläche geht gegen Null

Sehr langes Rechteck ($a \gg b$):
• Quadrat-Seitenlänge: $s = \sqrt{ab} \ll a$
• Das Quadrat ist viel "kompakter" als das Rechteck

Goldenes Rechteck ($a:b = \phi:1$):
• Quadrat-Seitenlänge: $s = \sqrt{\phi \cdot 1} = \sqrt{\phi} \approx 1{,}272$

Praktische Anwendungen

Landwirtschaft und Gartenbau:
• Umwandlung rechteckiger Felder in quadratische für bessere Bewirtschaftung
• Optimierung der Bewässerung (quadratische Felder sind effizienter)
• Zaunplanung: Quadrate benötigen weniger Zaun bei gleicher Fläche

Bauwesen und Architektur:
• Umplanung von Grundrissen bei gleichbleibender Wohnfläche
• Optimierung von Raumaufteilungen
• Materialberechnung für Bodenbeläge

Design und Grafik:
• Formatumwandlung bei gleichbleibender Bildfläche
• Layout-Optimierung für verschiedene Medien
• Proportionsplanung in der Typografie

Industrie und Produktion:
• Optimierung von Lagerflächen
• Materialzuschnitt und Abfallminimierung
• Produktionslinien-Planung

Umkehrrechnung: Quadrat zu Rechteck

Die Umkehrung ist nicht eindeutig, da unendlich viele Rechtecke dieselbe Fläche haben können:

Gegeben: Quadrat mit Seitenlänge $s$
Gesucht: Rechteck mit gleicher Fläche

Bedingung: $a \times b = s^2$

Mögliche Rechtecke:
• $a = s, b = s$ (das ursprüngliche Quadrat)
• $a = 2s, b = \frac{s}{2}$ (2:1-Rechteck)
• $a = 4s, b = \frac{s}{4}$ (4:1-Rechteck)
• Allgemein: $a = ks, b = \frac{s}{k}$ für beliebiges $k > 0$

Optimierungsaspekte

Warum das Quadrat optimal ist:
• Minimaler Umfang: Bei gegebener Fläche hat das Quadrat den kleinsten Umfang
• Isoperimetrisches Problem: Umgekehrt hat das Quadrat bei gegebenem Umfang die größte Fläche
• Symmetrie: Alle Richtungen sind gleichberechtigt
• Stabilität: Quadratische Strukturen sind mechanisch stabiler

Mathematischer Beweis (Umfang-Minimierung):
Für gegebene Fläche $A = ab$ ist der Umfang $U = 2(a + b)$.
Mit der Nebenbedingung $b = \frac{A}{a}$ wird:
$$U(a) = 2\left(a + \frac{A}{a}\right)$$
Minimum bei $\frac{dU}{da} = 0$:
$$\frac{dU}{da} = 2\left(1 - \frac{A}{a^2}\right) = 0$$ $$\Rightarrow a^2 = A \Rightarrow a = \sqrt{A}$$
Also: $a = b = \sqrt{A}$ (Quadrat!)

Verwandte mathematische Konzepte

Geometrisches und arithmetisches Mittel:
• Quadrat-Seitenlänge = Geometrisches Mittel: $\sqrt{ab}$
• Halbachsen-Mittelwert = Arithmetisches Mittel: $\frac{a+b}{2}$
• Es gilt immer: $\sqrt{ab} \leq \frac{a+b}{2}$ (AM-GM-Ungleichung)

Flächenformeln für andere Formen:
• Kreis mit gleicher Fläche: $r = \sqrt{\frac{ab}{\pi}}$
• Gleichseitiges Dreieck: $s = \sqrt{\frac{4ab}{\sqrt{3}}}$
• Regelmäßiges Sechseck: $s = \sqrt{\frac{2ab}{3\sqrt{3}}}$

Dimensionsanalyse:
• Eingabe: Längen [L]
• Fläche: [L²]
• Quadratwurzel bringt zurück zu [L]
• Mathematisch konsistent und physikalisch sinnvoll

Fehlerquellen und Hinweise

Häufige Missverständnisse:
• ❌ Umfang bleibt gleich (falsch: Fläche bleibt gleich)
• ❌ Diagonale bleibt gleich (falsch: nur bei bereits quadratischen Rechtecken)
• ❌ Seitenverhältnis bleibt erhalten (falsch: wird immer 1:1)

Berechnungshinweise:
• Bei sehr unterschiedlichen Seitenlängen können Rundungsfehler auftreten
• Negative Eingabewerte sind physikalisch nicht sinnvoll
• Sehr kleine oder große Werte sollten in wissenschaftlicher Notation eingegeben werden

Validierung der Ergebnisse:
• Kontrollrechnung: $s^2 = a \times b$
• Plausibilitätsprüfung: $s$ sollte zwischen $\min(a,b)$ und $\max(a,b)$ liegen
• Bei $a = b$ muss $s = a = b$ sein

Geometrie Rechner 2D Runde Formen

Kreis

Dreiecke

Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)

Spezielle Vierecke

Quadrat
Rechteck
Parallelogramm
Raute
Trapez
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rechteckiger Rahmen
Konkaves Viereck Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt

Polygone

Pentagon (Fünfeck)
Hexagon (Sechseck)
Heptagon (Siebeneck)

Allgemeine Vierecke

Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)