Dreieck im Koordinatensystem Rechner

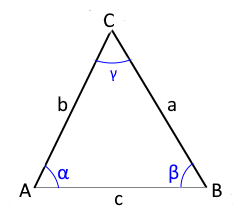
Dreieck im Koordinatensystem

Ein Dreieck im Koordinatensystem wird durch die Koordinaten seiner drei Eckpunkte $A(x_A, y_A)$, $B(x_B, y_B)$ und $C(x_C, y_C)$ vollständig bestimmt. Aus diesen Koordinaten lassen sich alle geometrischen Eigenschaften des Dreiecks berechnen.

Grundbegriffe:

• Eckpunkte: $A(x_A, y_A)$, $B(x_B, y_B)$, $C(x_C, y_C)$
• Seitenlängen: $a$ (BC), $b$ (AC), $c$ (AB)
• Winkel: $\alpha$ (bei A), $\beta$ (bei B), $\gamma$ (bei C)
• Schwerpunkt: Schnittpunkt der Seitenhalbierenden

Formeln für Dreiecke im Koordinatensystem

Seitenlängen (Abstandsformel):
$$a = |BC| = \sqrt{(x_C - x_B)^2 + (y_C - y_B)^2}$$ $$b = |AC| = \sqrt{(x_C - x_A)^2 + (y_C - y_A)^2}$$ $$c = |AB| = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2}$$
Fläche (Shoelace-Formel):
$$A = \frac{1}{2} |x_A(y_B - y_C) + x_B(y_C - y_A) + x_C(y_A - y_B)|$$
Alternative Flächenformel (Kreuzprodukt):
$$A = \frac{1}{2} |\vec{AB} \times \vec{AC}|$$ $$A = \frac{1}{2} |(x_B - x_A)(y_C - y_A) - (x_C - x_A)(y_B - y_A)|$$
Schwerpunkt:
$$S = \left(\frac{x_A + x_B + x_C}{3}, \frac{y_A + y_B + y_C}{3}\right)$$
Umfang:
$$U = a + b + c$$

Winkelberechnung

Winkel mit Vektoren:
$$\cos \alpha = \frac{\vec{AB} \cdot \vec{AC}}{|\vec{AB}| \cdot |\vec{AC}|}$$ $$\cos \beta = \frac{\vec{BA} \cdot \vec{BC}}{|\vec{BA}| \cdot |\vec{BC}|}$$ $$\cos \gamma = \frac{\vec{CA} \cdot \vec{CB}}{|\vec{CA}| \cdot |\vec{CB}|}$$
wobei das Skalarprodukt zweier Vektoren $\vec{u} = (u_x, u_y)$ und $\vec{v} = (v_x, v_y)$: $$\vec{u} \cdot \vec{v} = u_x \cdot v_x + u_y \cdot v_y$$

Beispielrechnung

Gegeben: $A(1, 2)$, $B(5, 2)$, $C(3, 6)$

Seitenlängen berechnen:
$a = |BC| = \sqrt{(3-5)^2 + (6-2)^2} = \sqrt{4 + 16} = \sqrt{20} \approx 4{,}47$
$b = |AC| = \sqrt{(3-1)^2 + (6-2)^2} = \sqrt{4 + 16} = \sqrt{20} \approx 4{,}47$
$c = |AB| = \sqrt{(5-1)^2 + (2-2)^2} = \sqrt{16 + 0} = 4$

Fläche berechnen (Shoelace):
$A = \frac{1}{2} |1(2-6) + 5(6-2) + 3(2-2)|$
$A = \frac{1}{2} |1(-4) + 5(4) + 3(0)| = \frac{1}{2} |-4 + 20 + 0| = \frac{1}{2} \cdot 16 = 8$

Umfang berechnen:
$U = a + b + c = 4{,}47 + 4{,}47 + 4 \approx 12{,}94$

Schwerpunkt berechnen:
$S = \left(\frac{1+5+3}{3}, \frac{2+2+6}{3}\right) = \left(\frac{9}{3}, \frac{10}{3}\right) = (3, 3{,}33)$

Besondere Eigenschaften

Kollinearität prüfen:
Drei Punkte sind kollinear (liegen auf einer Geraden), wenn die Fläche des Dreiecks null ist: $$x_A(y_B - y_C) + x_B(y_C - y_A) + x_C(y_A - y_B) = 0$$
Orientierung:
• Ist der Ausdruck positiv: Punkte sind gegen den Uhrzeigersinn angeordnet
• Ist der Ausdruck negativ: Punkte sind im Uhrzeigersinn angeordnet
• Ist der Ausdruck null: Punkte sind kollinear

Weitere wichtige Punkte

Umkreismittelpunkt:
Der Mittelpunkt des Umkreises liegt im Schnittpunkt der Mittelsenkrechten der Seiten.

Inkreismittelpunkt:
Der Mittelpunkt des Inkreises liegt im Schnittpunkt der Winkelhalbierenden.

Höhenschnittpunkt (Orthozentrum):
Schnittpunkt der drei Höhen des Dreiecks.

Eulergerade:
Schwerpunkt, Umkreismittelpunkt und Höhenschnittpunkt liegen auf einer Geraden.

Praktische Anwendungen

Dreiecke im Koordinatensystem sind wichtig für:

• Computergrafik: 3D-Modellierung, Triangulation
• Vermessung: Triangulation, GPS-Berechnungen
• Architektur: CAD-Systeme, Konstruktionspläne
• Robotik: Pfadplanung, Navigation
• Spieleentwicklung: Kollisionserkennung, Physik-Engines
• Kartographie: Landkarten, GIS-Systeme

Vektorrechnung im Dreieck

Wichtige Vektoren:
• Seitenvektor: $\vec{AB} = (x_B - x_A, y_B - y_A)$
• Betrag eines Vektors: $|\vec{AB}| = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2}$
• Einheitsvektor: $\hat{AB} = \frac{\vec{AB}}{|\vec{AB}|}$

Skalarprodukt:
$$\vec{u} \cdot \vec{v} = |\vec{u}| \cdot |\vec{v}| \cdot \cos \theta$$ wobei $\theta$ der Winkel zwischen den Vektoren ist.

Kreuzprodukt (2D):
$$\vec{u} \times \vec{v} = u_x \cdot v_y - u_y \cdot v_x$$ Das Kreuzprodukt gibt die (vorzeichenbehaftete) Fläche des Parallelogramms an.

Geometrie Rechner 2D Runde Formen

Kreis

Dreiecke

Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)

Spezielle Vierecke

Quadrat
Rechteck
Parallelogramm
Raute
Trapez
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rechteckiger Rahmen
Konkaves Viereck Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt

Polygone

Pentagon (Fünfeck)
Hexagon (Sechseck)
Heptagon (Siebeneck)

Allgemeine Vierecke

Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)