Drachenviereck Flächeninhalt Rechner

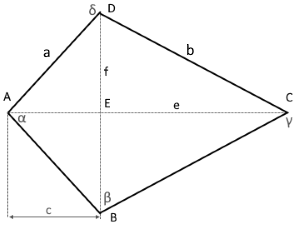
Drachenviereck-Eigenschaften

• Einfache Formel: A = ½ × p × q
• Senkrechte Diagonalen: p ⊥ q
• Nur 2 Werte nötig: Keine komplexen Berechnungen

Drachenviereck Flächenformel - Einfach und Schnell

Der Flächeninhalt eines Drachenvierecks (auch Deltoid oder Tangentenviereck genannt) lässt sich mit einer der einfachsten Formeln der Geometrie berechnen. Sie benötigen nur die beiden Diagonalen!

Praktische Berechnungsbeispiele

Besondere Eigenschaften der Drachenviereck-Fläche

Unabhängigkeit von anderen Parametern:
• Die Fläche hängt nur von den Diagonalen ab
• Seitenlängen, Winkel oder Position sind irrelevant
• Jedes Drachenviereck mit denselben Diagonalen hat dieselbe Fläche
• Die Formel gilt für alle Drachenvierecke, auch unregelmäßige

Vergleich mit anderen Vierecken

Häufige Anwendungsfälle

Tipps zur korrekten Messung

So messen Sie die Diagonalen richtig:
• Die Diagonalen sind die Verbindungslinien zwischen gegenüberliegenden Ecken
• Beide Diagonalen müssen vollständig gemessen werden
• Bei physischen Objekten: Maßband oder Laser-Entfernungsmesser
• Bei technischen Zeichnungen: Direkte Bemaßung ablesen
• Bei Koordinaten: Abstand zwischen gegenüberliegenden Punkten berechnen

Fehlerquellen vermeiden

Häufige Berechnungsfehler:
• Falsche Diagonalen: Nicht zwischen gegenüberliegenden Ecken
• Vergessener Faktor ½: Vollprodukt statt halbem Produkt
• Einheitenfehler: Verschiedene Maßeinheiten für p und q
• Verwechslung: Diagonale mit Seitenlänge verwechselt

Erweiterte Berechnungen

Was Sie zusätzlich berechnen können:
Wenn Sie nur den Flächeninhalt kennen:
• Bei bekannter Diagonale p: q = 2A/p
• Bei bekannter Diagonale q: p = 2A/q
• Verhältnis der Diagonalen: p:q bei gegebener Fläche

Mathematische Hintergründe

Warum steht der Faktor ½ in der Formel?
Das Drachenviereck lässt sich als Kombination von vier rechtwinkligen Dreiecken darstellen. Jedes Dreieck hat die Fläche ½ × Kathete₁ × Kathete₂. Die Summe aller vier Dreiecke ergibt ½ × p × q.

Drachenviereck in der Praxis

Reale Beispiele für Drachenvierecke:
• Papierdrachen: Klassische Drachenform mit zwei Diagonalen
• Schmucksteine: Deltaförmige Edelsteinschliffe
• Dachgauben: Architektonische Elemente
• Verkehrsschilder: Spezielle Warnschilder
• Kachelmuster: Dekorative Fliesenverlegung
• Briefmarken: Sonderformen historischer Marken

Beziehung zu anderen geometrischen Formen

Das Drachenviereck als Sonderfall:
• Raute: Drachenviereck mit gleichen Seitenlängen
• Quadrat: Raute mit rechten Winkeln
• Rechteck: Drachenviereck mit gleichen Diagonalen
• Parallelogramm: Drachenviereck ohne senkrechte Diagonalen
• Trapez: Drachenviereck mit einer parallelen Seitenseite

Geometrie Rechner 2D Runde Formen

Kreis

Dreiecke

Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)

Spezielle Vierecke

Quadrat
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt

Polygone

N-Eck (Universal)
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)

Allgemeine Vierecke

Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)