Trapez Diagonale p Rechner

Spezialisierter Rechner für Trapez-Diagonale p


📍 Trapez Diagonale p Rechner

Hauptdiagonale - Spezialberechnung

🔀 Trapez-Typ wählen
Einheiten
Einheiten
Einheiten
📐
Formel-Auswahl: Rechtwinklig: $p =\sqrt{h^2 + a^2}$ Symmetrisch: $p = \sqrt{h^2 + \left(\frac{a+b}{2}\right)^2}$
⚠️ Fehler:

Geben Sie die drei Werte ein: untere Basis $a$, obere Basis $b$ und Höhe $h$. Wählen Sie den Trapez-Typ und der Rechner berechnet die Diagonale $p$.

Eingaberegeln

• Basis $a$ (untere parallele Seite)
• Basis $b$ (obere parallele Seite)
• Höhe $h$ (senkrechter Abstand)
• Dezimalzahlen mit Punkt oder Komma
• Alle Werte müssen positiv sein


Trapez mit Diagonale p


Trapez-Typen

Symmetrisch: Beide Schenkel gleich lang, Diagonale durch Mittelwert der Basen
Rechtwinklig: Ein Schenkel senkrecht zu den Basen, präzise Berechnung

Diagonale $p$

• Hauptdiagonale: Verbindet untere linke mit oberer rechter Ecke
• Symmetrisch: $p = \sqrt{h^2 + \left(\frac{a+b}{2}\right)^2}$
• Rechtwinklig: $p = \sqrt{h^2 + a^2}$


Trapez-Diagonale $p$ berechnen

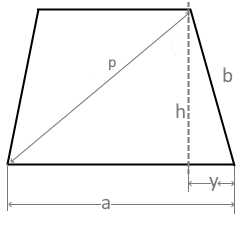
Die Diagonale $p$ eines Trapezes ist eine der beiden Diagonalen, die die gegenüberliegenden Eckpunkte verbindet. Speziell verbindet die Diagonale $p$ die untere linke Ecke mit der oberen rechten Ecke des Trapezes.

📍 Diagonale p Eigenschaften
  • • Hauptdiagonale: Unten links → oben rechts
  • • Länge abhängig: Von Trapez-Typ
  • • Symmetrisch: Durch Basenmittelwert
  • • Rechtwinklig: Pythagoras mit ganzer Basis
🔄 Berechnungstypen
  • • Symmetrisch: Gleichschenklig, zentriert
  • • Rechtwinklig: 90°-Winkel, vereinfacht
  • • Automatische Auswahl: Je nach Typ
  • • Optimierte Formeln: Höchste Präzision

Berechnungsformeln nach Trapez-Typ

📊 Formeln für Diagonale p:

Symmetrisches (gleichschenkliges) Trapez:
$$p = \sqrt{h^2 + \left(\frac{a+b}{2}\right)^2}$$ Bei symmetrischen Trapezen ist die obere Basis mittig ausgerichtet.

Rechtwinkliges Trapez:
$$p = \sqrt{h^2 + a^2}$$ Wenn ein Schenkel senkrecht steht, vereinfacht sich die Berechnung.

Allgemeine Formel:
$$p = \sqrt{h^2 + (a - x)^2}$$ wobei $x$ die horizontale Verschiebung der oberen Basis ist.

Berechnungsbeispiele

📝 Beispielrechnungen mit $a = 10$ cm, $b = 6$ cm, $h = 4$ cm:

Symmetrisches Trapez:
$p = \sqrt{h^2 + \left(\frac{a+b}{2}\right)^2} = \sqrt{4^2 + \left(\frac{10+6}{2}\right)^2}$
$p = \sqrt{16 + 64} = \sqrt{80} = 8{,}94$ cm

Rechtwinkliges Trapez:
$p = \sqrt{h^2 + a^2} = \sqrt{4^2 + 10^2}$
$p = \sqrt{16 + 100} = \sqrt{116} = 10{,}77$ cm

Unterschied:
Die rechtwinklige Berechnung ergibt eine längere Diagonale (10,77 cm vs. 8,94 cm),
da sie die volle untere Basis $a$ berücksichtigt.

Trapez-Typen im Detail

🟢 Symmetrische Trapeze
  • • Gleiche Schenkel: Beide gleich lang
  • • Gleiche Diagonalen: p = q
  • • Zentrierte Basis: Obere Basis mittig
  • • Gleiche Basiswinkel: α = β
🔴 Rechtwinklige Trapeze
  • • Rechter Winkel: Ein Schenkel senkrecht
  • • Höhe = Schenkel: h entspricht Senkrechter
  • • Vereinfachte Berechnung: Durch 90°
  • • Verschiedene Diagonalen: p ≠ q

Praktische Anwendungen

🏗️ Konstruktion
  • • Stabilisierung von Trapez-Rahmen
  • • Dachsparren-Berechnung
  • • Verstrebungen dimensionieren
  • • Statische Berechnungen
🔬 Technische Anwendung
  • • Maschinenbau-Komponenten
  • • Architektonische Analysen
  • • Geometrische Beweise
  • • CAD-System Berechnungen
🌟 Trapez-Diagonale p - Spezialisierte Berechnung:
  • Hauptdiagonale: Verbindet strategisch wichtige Eckpunkte
  • Typ-abhängige Formeln: Optimiert für symmetrische und rechtwinklige Trapeze
  • Konstruktive Relevanz: Wichtig für Stabilität und Festigkeitsberechnungen
  • Präzise Berechnung: Berücksichtigt Trapez-spezifische Geometrie
  • Praktische Anwendung: Von Architektur bis Maschinenbau
Geometrie Rechner 2D Runde Formen
Kreis
Dreiecke
Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)
Spezielle Vierecke
Quadrat
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt
Polygone
N-Eck (Universal)
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)
Allgemeine Vierecke
Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)