Rechteckiger Rahmen Rechner

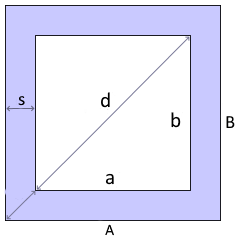
Der rechteckige Rahmen

Ein rechteckiger Rahmen ist eine rechteckige Umrandung, die aus einem größeren Rechteck (Außenmaße) und einem kleineren Rechteck (Innenmaße) besteht. Die Differenz zwischen beiden bildet die eigentliche Rahmenfläche. Solche Rahmen finden sich bei Bilderrahmen, Fensterrahmen, Türrahmen und vielen anderen Anwendungen.

Charakteristische Eigenschaften:

• Außenrechteck: Definiert durch Außenbreite $B$ und Außenhöhe $H$
• Innenrechteck: Definiert durch Innenbreite $b$ und Innenhöhe $h$
• Gleichmäßige Rahmenstärke: $s = \frac{B-b}{2} = \frac{H-h}{2}$
• Symmetrische Anordnung: Rahmen ist rundum gleich stark
• Materialverbrauch: Entspricht der Rahmenfläche

Grundlegende Formeln

Spezielle Berechnungsverfahren

Beispielrechnung

Praktische Anwendungen

Elektronik und Design:
• Gehäusedesign mit Wandstärken
• Display-Rahmen bei Monitoren und Tablets
• Verpackungsdesign mit Materialoptimierung
• Architektonische Rahmenelemente

Handwerk und Fertigung:
• Zuschnittoptimierung bei der Materialplanung
• Kalkulationen für Serienfertigung
• Qualitätskontrolle von Rahmenmaßen
• Toleranzberechnungen in der Produktion

Erweiterte Berechnungen

Diagonalen der Rechtecke:
$$d_{außen} = \sqrt{B^2 + H^2} \quad \text{(Außendiagonale)}$$ $$d_{innen} = \sqrt{b^2 + h^2} \quad \text{(Innendiagonale)}$$
Seitenverhältnisse:
$$\text{Außenverhältnis} = \frac{B}{H}, \quad \text{Innenverhältnis} = \frac{b}{h}$$
Materialeffizienz:
$$\text{Effizienz} = \frac{A_{rahmen}}{A_{außen}} = 1 - \frac{A_{innen}}{A_{außen}}$$
Optimale Rahmenstärke:
Für gegebene Außenmaße und gewünschte Materialfläche: $$s = \frac{(B + H) - \sqrt{(B + H)^2 - 4A_{rahmen}}}{4}$$

Materialberechnungen

Lineare Materialverteilung:
Für Rahmenprofile, die aus vier Leisten zusammengesetzt werden: $$\text{Material}_{linear} = 2B + 2H \quad \text{(Außenumfang)}$$ Berücksichtigung von Gehrungsschnitten: zusätzliche Verschnittlänge

Verschnitt bei Gehrungen:
Pro Ecke geht Material durch den 45°-Schnitt verloren: $$\text{Verschnitt} = 4 \times s \times \sqrt{2} \quad \text{(bei 45° Gehrung)}$$
Plattenförmiges Material:
Bei Ausschneiden aus einer größeren Platte: $$\text{Abfall} = \text{Plattenfläche} - A_{außen}$$
Kostenoptimierung:
Optimale Ausnutzung von Standardgrößen: $$\text{Stückzahl} = \left\lfloor \frac{\text{Standardplatte}}{A_{außen}} \right\rfloor$$

Toleranzen und Fertigungsaspekte

Maßtoleranzen:
In der Praxis müssen Fertigungstoleranzen berücksichtigt werden: $$s_{praktisch} = s_{nominal} \pm \Delta s$$
Fugenzugaben:
Bei zusammengesetzten Rahmen: • Klebefugen: typisch 0,1-0,2 mm
• Schweißnähte: typisch 0,5-2 mm
• Schraubverbindungen: typisch 1-5 mm

Materialbedingte Anpassungen:
• Holz: Berücksichtigung der Faserrichtung
• Metall: Biegradien bei scharfen Kanten
• Kunststoff: Schrumpfung beim Abkühlen
• Verbundmaterialien: Schichtaufbau

Qualitätskontrolle:
Prüfmaße für die Fertigung: $$\text{Rechtwinkligkeit} = |d_1 - d_2| < \text{Toleranz}$$ wobei $d_1$ und $d_2$ die beiden Diagonalen sind

Konstruktionsvarianten

Einfacher Rahmen:
Gleichmäßige Rahmenstärke rundum, rechteckige Querschnitte

Stufenrahmen:
Verschiedene Rahmenstärken für unterschiedliche Funktionen: $$s_{oben/unten} \neq s_{links/rechts}$$
Profilrahmen:
Komplexe Querschnitte mit Nuten, Falzen oder Verzierungen: • L-Profile für einfache Aufnahme
• U-Profile für Glaseinlagerung
• T-Profile für Verbindungen
• Kombinationsprofile für Mehrfachfunktionen

Hohlrahmen:
Rahmen mit innenliegenden Hohlräumen: $$A_{material} = A_{außen} - A_{innen} - A_{hohlraum}$$
Mehrschichtrahmen:
Rahmen aus mehreren Materiallagen: $$\text{Gesamtstärke} = \sum_{i=1}^{n} s_i$$

Spezielle Geometrien

Quadratische Rahmen:
Wenn $B = H$, vereinfachen sich die Formeln: $$A_{rahmen} = B^2 - b^2 = (B-b)(B+b) = 2s(2B-2s) = 4s(B-s)$$
Schmale Rahmen:
Für $s \ll B, H$ (Näherung für dünne Rahmen): $$A_{rahmen} \approx 2s(B + H - 2s) \approx 2s(B + H)$$
Breite Rahmen:
Für $s$ vergleichbar mit $B, H$ müssen alle Terme berücksichtigt werden.
Goldener Schnitt im Rahmendesign:
Optimale Proportionen für Bilderrahmen: $$\frac{B}{H} = \phi = \frac{1 + \sqrt{5}}{2} \approx 1{,}618$$
Minimaler Materialverbrauch:
Für gegebene Innenfläche und Rahmenstärke ist das quadratische Format optimal: $$\frac{\partial A_{rahmen}}{\partial B} = 0 \Rightarrow B = H$$

Berechnungstools und Software

CAD-Integration:
Automatische Rahmenberechnung in Konstruktionsprogrammen: • Parametrische Modellierung
• Automatische Stücklisten
• Materialverbrauchsanalyse
• Kostenrechnung

Fertigungsoptimierung:
• Schnittoptimierung für Abfallminimierung
• Reihenfolgenplanung der Bearbeitung
• Werkzeugauswahl und -verschleiß
• Qualitätssicherung durch Messtechnik

Online-Konfiguratoren:
Kundenspezifische Rahmenberechnungen: • Echtzeitpreise basierend auf Maßen
• Materialauswahl und -eigenschaften
• Visualisierung des Endergebnisses
• Automatische Angebotserstellung

Geometrie Rechner 2D Runde Formen

Kreis

Dreiecke

Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)

Spezielle Vierecke

Quadrat
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt

Polygone

N-Eck (Universal)
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)

Allgemeine Vierecke

Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)