Rechteck Rechner

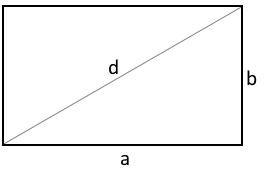
Das Rechteck

Ein Rechteck ist ein Viereck mit vier rechten Winkeln (90°). Die gegenüberliegenden Seiten sind parallel und gleich lang. Das Rechteck ist eine der grundlegendsten geometrischen Formen und kommt in vielen praktischen Anwendungen vor.

Eigenschaften:

• Vier rechte Winkel: $\alpha = \beta = \gamma = \delta = 90°$
• Gegenüberliegende Seiten gleich: $a_1 = a_2$ und $b_1 = b_2$
• Zwei Symmetrieachsen: durch die Mittelpunkte der Seiten
• Punktsymmetrie: zum Mittelpunkt
• Diagonalen: gleich lang, halbieren sich

Formeln für das Rechteck

Grundformeln mit Länge $a$ und Breite $b$:

Fläche:
$$A = a \cdot b$$
Umfang:
$$U = 2(a + b) = 2a + 2b$$
Diagonale (Pythagoras):
$$d = \sqrt{a^2 + b^2}$$
Alternative Flächenformel:
$$A = \frac{d^2 \sin(2\alpha)}{2}$$ wobei $\alpha$ der Winkel zwischen Diagonale und einer Seite ist.

Alle möglichen Rechenwege

Aus Länge und Breite:
• Fläche: $A = a \cdot b$
• Umfang: $U = 2(a + b)$
• Diagonale: $d = \sqrt{a^2 + b^2}$

Aus Fläche und Länge:
• Breite: $b = \frac{A}{a}$
• Umfang: $U = 2a + \frac{2A}{a}$
• Diagonale: $d = \sqrt{a^2 + \left(\frac{A}{a}\right)^2}$

Aus Umfang und Länge:
• Breite: $b = \frac{U}{2} - a$
• Fläche: $A = a \cdot \left(\frac{U}{2} - a\right)$
• Diagonale: $d = \sqrt{a^2 + \left(\frac{U}{2} - a\right)^2}$

Aus Diagonale und Länge:
• Breite: $b = \sqrt{d^2 - a^2}$
• Fläche: $A = a \cdot \sqrt{d^2 - a^2}$
• Umfang: $U = 2a + 2\sqrt{d^2 - a^2}$

Aus Fläche und Umfang:
Lösung der quadratischen Gleichung: $a^2 - \frac{U}{2}a + A = 0$
• $a = \frac{U/2 + \sqrt{(U/2)^2 - 4A}}{2}$
• $b = \frac{U/2 - \sqrt{(U/2)^2 - 4A}}{2}$
• Diagonale: $d = \sqrt{a^2 + b^2}$

Beispielrechnung

Gegeben: Länge $a = 8$ cm, Breite $b = 6$ cm

Fläche berechnen:
$A = a \times b = 8 \times 6 = 48$ cm²

Umfang berechnen:
$U = 2(a + b) = 2(8 + 6) = 2 \times 14 = 28$ cm

Diagonale berechnen:
$d = \sqrt{a^2 + b^2} = \sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10$ cm

Kontrolle mit 3-4-5-Dreieck:
Das Verhältnis 6:8:10 entspricht 3:4:5, einem bekannten rechtwinkligen Dreieck.

Spezialfall: Quadrat

Ein Quadrat ist ein spezielles Rechteck mit $a = b$:
• Fläche: $A = a^2$
• Umfang: $U = 4a$
• Diagonale: $d = a\sqrt{2}$

Übergang vom Rechteck zum Quadrat:
Wenn sich Länge und Breite angleichen, wird das Rechteck immer "quadratischer", bis es bei $a = b$ zum perfekten Quadrat wird.

Besondere Eigenschaften

Symmetrie:

• Das Rechteck hat 2 Symmetrieachsen (parallel zu den Seiten)
• Es ist punktsymmetrisch zum Mittelpunkt
• Drehsymmetrie: 2-zählig (180°)
• Die Diagonalen halbieren sich, aber stehen nicht senkrecht aufeinander

Verhältnisse:

• Seitenverhältnis: $a : b$ (charakterisiert die Form)
• Goldener Schnitt: $a : b = \phi : 1 \approx 1{,}618 : 1$
• DIN-Format: $a : b = \sqrt{2} : 1 \approx 1{,}414 : 1$

Praktische Anwendungen

Rechtecke sind überall in unserem Leben zu finden:

• Architektur: Grundrisse, Fenster, Türen, Zimmer
• Technik: Bildschirme, Displays, Platinen, Bauteile
• Alltag: Bücher, Papier, Tische, Spiegel
• Sport: Fußballfelder, Tennisplätze, Schwimmbecken
• Kunst: Leinwände, Bilderrahmen, Layouts
• Landwirtschaft: Felder, Gärten, Gewächshäuser

Konstruktion und Anwendung

Konstruktion eines Rechtecks:
1. Zeichne eine Gerade und markiere die Länge $a$
2. Errichte an beiden Endpunkten Senkrechte
3. Trage auf beiden Senkrechten die Breite $b$ ab
4. Verbinde die Endpunkte zur vierten Seite

Flächenoptimierung:
Bei gegebenem Umfang hat das Quadrat die größte Fläche aller Rechtecke.
Bei gegebener Fläche hat das Quadrat den kleinsten Umfang aller Rechtecke.

Verwandte geometrische Formen

Parallelogramm:
Das Rechteck ist ein spezielles Parallelogramm mit rechten Winkeln.

Rhombus:
Wenn ein Rhombus rechte Winkel hat, wird es zum Quadrat.

Trapez:
Ein Rechteck ist auch ein spezielles Trapez mit zwei parallelen Seitenpaaren.

Rechteckige Koordinatensysteme:
Das kartesische Koordinatensystem basiert auf der rechtwinkligen Struktur des Rechtecks.

Mathematische Besonderheiten

Flächeninhalt und Optimierung:
• Maximum: Bei festem Umfang maximiert das Quadrat die Fläche
• Minimum: Bei fester Fläche minimiert das Quadrat den Umfang
• Verhältnis: $\frac{\text{Fläche}}{\text{Umfang}^2} = \frac{ab}{4(a+b)^2}$

Diagonaleneigenschaften:
• Beide Diagonalen sind gleich lang: $d_1 = d_2$
• Sie halbieren sich im Mittelpunkt
• Winkel zwischen den Diagonalen: $\alpha = 2 \arctan\left(\frac{b}{a}\right)$

Seitenverhältnisse:
• Goldener Schnitt: $\frac{\text{a}}{\text{b}} = \frac{1 + \sqrt{5}}{2} \approx 1{,}618$
• DIN A-Format: $\frac{\text{a}}{\text{b}} = \sqrt{2} \approx 1{,}414$
• 16:9 (Breitbild): $\frac{\text{a}}{\text{b}} = \frac{16}{9} \approx 1{,}778$

Geometrie Rechner 2D Runde Formen

Kreis

Dreiecke

Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)

Spezielle Vierecke

Quadrat
Rechteck
Parallelogramm
Raute
Trapez
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rechteckiger Rahmen
Konkaves Viereck Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt

Polygone

Pentagon (Fünfeck)
Hexagon (Sechseck)
Heptagon (Siebeneck)

Allgemeine Vierecke

Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)