Hexagon Rechner

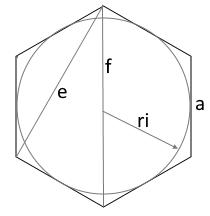
Das Hexagon (Regelmäßiges Sechseck)

Ein Hexagon ist ein regelmäßiges Sechseck mit sechs gleichen Seiten und sechs gleichen Innenwinkeln. Es ist eine der effizientesten Formen in der Natur und Technik, da es eine Fläche lückenlos füllen kann (Parkettierung).

Eigenschaften:

• Sechs gleiche Seiten: alle Seiten haben die Länge $a$
• Sechs gleiche Innenwinkel: jeder Winkel beträgt $120°$
• Sechs Symmetrieachsen: durch jede Ecke und Seitenmitte
• 6-zählige Rotationssymmetrie: alle 60° identisch
• Besonderheit: Der Umkreisradius ist gleich der Seitenlänge ($R=a$)

Grundlegende Formeln

Alle Berechnungen basieren auf der Seitenlänge $a$:

Innenwinkel:
$$\alpha = \frac{(6-2) \times 180°}{6} = 120°$$
Lange Diagonale:
$$d_l = 2a$$
Kurze Diagonale:
$$d_k = a \sqrt{3} \approx 1{,}732 \times a$$
Fläche:
$$A = \frac{3\sqrt{3}}{2} a^2 \approx 2{,}598 \times a^2$$
Umfang:
$$U = 6a$$
Inkreisradius:
$$r = \frac{\sqrt{3}}{2} a \approx 0{,}866 \times a$$
Umkreisradius:
$$R = a$$

Struktur aus gleichseitigen Dreiecken

Das regelmäßige Hexagon ist einzigartig, da es aus sechs gleichseitigen Dreiecken zusammengesetzt ist, die sich im Mittelpunkt treffen.

Flächenberechnung über Dreiecke:
Die Fläche eines gleichseitigen Dreiecks mit Seite $a$ ist $A_{Dreieck} = \frac{\sqrt{3}}{4}a^2$.
Die Gesamtfläche des Hexagons ist daher: $$A = 6 \times A_{Dreieck} = 6 \times \frac{\sqrt{3}}{4}a^2 = \frac{3\sqrt{3}}{2}a^2$$

Rückrechnungsformeln

Seitenlänge aus anderen Werten:
• Aus langer Diagonale: $$a = \frac{d_l}{2}$$ • Aus kurzer Diagonale: $$\displaystyle a = \frac{d_k}{\sqrt{3}} \approx 0{,}577 \times d_k$$ • Aus Fläche: $$\displaystyle a = \sqrt{\frac{2A}{3\sqrt{3}}} \approx 0{,}620 \times \sqrt{A}$$ • Aus Umfang: $$\displaystyle a = \frac{U}{6}$$ • Aus Inkreisradius: $$\displaystyle a = \frac{2r}{\sqrt{3}} \approx 1{,}155 \times r$$ • Aus Umkreisradius: $$\displaystyle a = R$$

Konstruktion des Hexagons

Einfache Konstruktion mit dem Zirkel:

1. Zeichne einen Kreis mit Radius $R$ (dieser wird die Seitenlänge $a$)
2. Wähle einen Punkt auf dem Kreis als erste Ecke
3. Trage den Radius $R$ sechsmal auf dem Kreis ab
4. Verbinde die sechs Punkte zu einem regelmäßigen Sechseck

Beispielrechnung

Gegeben: Seitenlänge $a = 5$ cm

Lange Diagonale berechnen:
$d_l = 2 \times a = 2 \times 5 = 10$ cm

Kurze Diagonale berechnen:
$d_k = a \sqrt{3} = 5 \times 1{,}732 \approx 8{,}66$ cm

Fläche berechnen:
$A = 2{,}598 \times a^2 = 2{,}598 \times 25 \approx 64{,}95$ cm²

Umfang berechnen:
$U = 6 \times a = 6 \times 5 = 30$ cm

Inkreisradius berechnen:
$r = 0{,}866 \times a = 0{,}866 \times 5 \approx 4{,}33$ cm

Umkreisradius berechnen:
$R = a = 5$ cm

Praktische Anwendungen

Hexagone sind aufgrund ihrer Effizienz weit verbreitet:

• Natur: Bienenwaben, Schneeflocken, Basaltsäulen
• Technik: Schraubenköpfe und Muttern, Werkzeuge (Inbusschlüssel)
• Architektur: Fliesen, Kacheln, stabile Strukturen
• Chemie: Benzolringe und andere aromatische Verbindungen
• Spiele: Spielbretter (z.B. Siedler von Catan)

Mathematische Besonderheiten

Perfekte Parkettierung:
Regelmäßige Hexagone können die Ebene lückenlos und ohne Überlappungen füllen (tessellieren), da ihr Innenwinkel von $120°$ ein Teiler von $360°$ ist ($3 \times 120° = 360°$). Dies macht sie zur effizientesten Form, um eine Fläche zu bedecken.

Platonische Körper:
Das Hexagon ist keine Seitenfläche eines platonischen Körpers, bildet aber die Basis für hexagonale Prismen und Pyramiden.

Verwandte Polygone

Andere regelmäßige Polygone:
• Dreieck (3 Seiten): $\alpha = 60°$
• Quadrat (4 Seiten): $\alpha = 90°$
• Pentagon (5 Seiten): $\alpha = 108°$
• Hexagon (6 Seiten): $\alpha = 120°$
• Octagon (8 Seiten): $\alpha = 135°$

Allgemeine Formel für n-Ecke:
$$\alpha = \frac{(n-2) \times 180°}{n}$$

Historisches und Kulturelles

Antike und Natur:
Schon in der Antike wurde die perfekte Form der Bienenwabe bewundert. Pappos von Alexandria bewies mathematisch, dass das Hexagon die effizienteste Form zur Füllung einer Ebene ist.

Symbolik:
• Symbol für Harmonie, Gleichgewicht und Effizienz
• In der Esoterik und Religion (z.B. Davidstern aus zwei Dreiecken)

Geometrie Rechner 2D Runde Formen

Kreis

Dreiecke

Dreieck
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)

Spezielle Vierecke

Quadrat
Rechteck
Parallelogramm
Raute
Trapez
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rechteckiger Rahmen
Konkaves Viereck Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt

Polygone

Pentagon (Fünfeck)
Hexagon (Sechseck)
Heptagon (Siebeneck)

Allgemeine Vierecke

Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)