Konkaves Hexagon Rechner
Online Rechner für einspringende Sechsecke
Geben Sie einen bekannte Werte ein. Der Rechner berechnet die fehlenden Eigenschaften des konkaven Sechsecks.
Eingabeformat
Dezimalzahlen können mit Punkt oder Komma eingegeben werden.
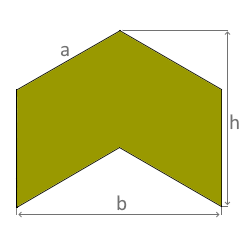
Das Konkave Hexagon (Einspringendes Sechseck)
Ein konkaves Hexagon ist ein sechsseitiges Polygon mit mindestens einem einspringenden Winkel > 180° (Reflexwinkel). Diese Geometrie erzeugt komplexe Formen mit einspringenden Ecken, die in Architektur, Design und Technik verwendet werden.
🔻 Konkavität
- • Reflexwinkel: Mindestens ein Winkel > 180°
- • Einspringende Ecke: Erzeugt "Delle" im Polygon
- • Winkelsumme: Immer exakt 720°
- • Komplexe Geometrie: Nicht konvex
Grundlegende Eigenschaften
📊 Mathematische Grundlagen:
Winkelsumme:
$$\sum_{i=1}^{6} \alpha_i = (6-2) \times 180° = 720°$$
Reflexwinkel-Bedingung:
$$\text{Mindestens ein } \alpha_i > 180°$$
Flächenberechnung :
$$A = \sqrt{3} \times a^2$$
Umfang:
$$U = \sum_{i=1}^{6} s_i = a + b + c + d + e + f$$
Inkreisradius:
$$r = \frac{\sqrt{3}}{2} a \approx 0{,}866 \times a$$
Umkreisradius:
$$R = a$$
Praktische Beispiele
📝 Beispielrechnung
Gegeben: Seitenlänge a = 6 cm
Lange Diagonale berechnen:
$d_l = 2 \times a = 2 \times 6 = 12$ cm
Kurze Diagonale berechnen:
$d_k = a \sqrt{3} = 6 \times 1{,}732 \approx 10{,}39$ cm
Fläche berechnen:
$A = \sqrt{3} \times a^2 = 1{,}732 \times 36 \approx 62{,}35$ cm²
Umfang berechnen:
$U = 6 \times a = 6 \times 6 = 36$ cm
Inkreisradius berechnen:
$r = 0{,}866 \times a = 0{,}866 \times 6 \approx 5{,}20$ cm
Umkreisradius berechnen:
$R = a = 6$ cm
Praktische Anwendungen
🏛️ Architektur & Design
- • Gebäude mit Innenhöfen
- • Atriumhäuser
- • Moderne Fassadengestaltung
- • Landschaftsarchitektur
🔧 Technik & Industrie
- • Maschinenbauteile mit Aussparungen
- • Stanzteile und Blechformen
- • Verpackungsdesign
- • CAD/CAM-Anwendungen
🔻 Besondere Eigenschaften konkaver Hexagone:
- Reflexwinkel: Mindestens ein Winkel > 180° erforderlich
- Anwendungsvielfalt: Architektur, Maschinenbau, Design
Geometrie Rechner
2D Runde Formen
KreisDreiecke
DreieckSpezielle Vierecke
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)
QuadratPolygone
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt
N-Eck (Universal)Allgemeine Vierecke
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)
Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)