Allgemeines Viereck Rechner
Online Rechner für unregelmäßige Vierecke - Eigenschaften und Formeln
Geben Sie die drei Seitenlängen (a, b, c) und zwei Winkel (β, γ) ein. Der Rechner berechnet automatisch die vierte Seite, alle Winkel, Diagonalen und Fläche.
Eingaberegeln
• Drei Seitenlängen (a, b, c) erforderlich
• Zwei Winkel (β, γ) in Grad eingeben
• Winkel zwischen 0° und 180°
• Dezimalzahlen mit Punkt oder Komma
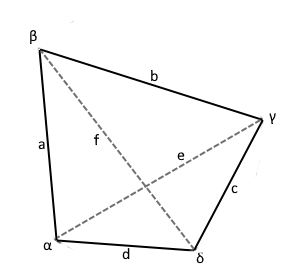
Das allgemeine Viereck
Ein allgemeines Viereck (auch unregelmäßiges Viereck genannt) ist ein Viereck ohne spezielle Symmetrieeigenschaften. Es ist die allgemeinste Form eines Vierecks und umfasst alle möglichen Vierecktypen als Spezialfälle.
🔷 Eigenschaften
- • Vier Seiten: Beliebige Längen a, b, c, d
- • Vier Winkel: α + β + γ + δ = 360°
- • Zwei Diagonalen: Verbinden gegenüberliegende Ecken
- • Bestimmung: Durch 5 unabhängige Parameter
📐 Berechnungsgrundlage
- • Eingabe: 3 Seiten + 2 Winkel
- • Kosinussatz: Für Diagonalen und 4. Seite
- • Bretschneider: Allgemeine Flächenformel
- • Winkelsumme: 4. Winkel automatisch berechnet
Formeln für das allgemeine Viereck
📊 Grundlegende Berechnungsformeln:
Diagonale e (Kosinussatz):
$$e = \sqrt{a^2 + b^2 - 2ab \cdot \cos(\beta)}$$
Diagonale f (Kosinussatz):
$$f = \sqrt{b^2 + c^2 - 2bc \cdot \cos(\gamma)}$$
Seite d (über Zwischenwinkel):
$$d = \sqrt{c^2 + e^2 - 2ce \cdot \cos(\gamma_2)}$$ $$\gamma_2 = \gamma - \gamma_1, \quad \gamma_1 = \arccos\left(\frac{b^2 + e^2 - a^2}{2be}\right)$$
Winkel α (Kosinussatz):
$$\alpha = \arccos\left(\frac{a^2 + d^2 - f^2}{2ad}\right)$$
Winkel δ (Winkelsumme):
$$\delta = 360° - \alpha - \beta - \gamma$$
Umfang:
$$U = a + b + c + d$$
Flächenberechnung
🔺 Bretschneider-Formel (Allgemein)
Für beliebige Vierecke mit Seiten a, b, c, d und Diagonalen e, f:
$$A = \frac{\sqrt{4e^2f^2 - (b^2 + d^2 - a^2 - c^2)^2}}{4}$$
Alternative Form mit Winkeln:
$$A = \sqrt{(s-a)(s-b)(s-c)(s-d) - abcd \cdot \cos^2\left(\frac{\alpha+\gamma}{2}\right)}$$ wobei $s = \frac{a+b+c+d}{2}$ der Halbumfang ist.
Spezialfälle:
• Bei Sehnenvierecken: $\alpha + \gamma = 180°$ → Brahmagupta-Formel
• Bei Tangentenvierecken: Spezielle Vereinfachungen möglich
• Bei Rechtecken: $A = ab$ (einfachste Form)
Praktisches Berechnungsbeispiel
📝 Beispielrechnung: Allgemeines Viereck
Gegeben: Seiten a = 7, b = 5, c = 6; Winkel β = 80°, γ = 70°
Diagonale e berechnen:
$e = \sqrt{7^2 + 5^2 - 2 \cdot 7 \cdot 5 \cdot \cos(80°)} = \sqrt{49 + 25 - 70 \cdot 0{,}174} \approx 7{,}86$
Diagonale f berechnen:
$f = \sqrt{5^2 + 6^2 - 2 \cdot 5 \cdot 6 \cdot \cos(70°)} = \sqrt{25 + 36 - 60 \cdot 0{,}342} \approx 6{,}36$
Klassifikation nach Eigenschaften
📋 Viereck-Hierarchie
Nach Konvexität:
• Konvexes Viereck: Alle Innenwinkel < 180°
• Konkaves Viereck: Ein Innenwinkel > 180°
• Selbstüberschneidendes Viereck: Seiten kreuzen sich
Nach Symmetrie:
• Drachenviereck: Zwei Paare gleicher benachbarter Seiten
• Trapezoid: Keine parallelen Seiten
• Trapez: Ein Paar parallele Seiten
• Parallelogramm: Zwei Paare parallele Seiten
Nach Umkreis:
• Zyklisches Viereck: Alle Eckpunkte auf einem Kreis
• Tangentenviereck: Alle Seiten tangential zu einem Kreis
• Bizyklisches Viereck: Sowohl zyklisch als auch tangential
Spezialfälle:
• Rechteck: Parallelogramm mit rechten Winkeln
• Raute: Parallelogramm mit gleichen Seiten
• Quadrat: Rechteck mit gleichen Seiten
Praktische Anwendungen
🏗️ Bauingenieurwesen
- • Atypische Grundrisse
- • Moderne Gebäudeformen
- • Brückenkonstruktionen
- • Dachgeometrien
📐 Vermessung
- • Unregelmäßige Grundstücke
- • Parzellenvermessung
- • Verwaltungsgrenzen
- • Katastervermessung
⚙️ Maschinenbau
- • Komplexe Bauteile
- • Freiformflächen
- • Werkzeuggeometrie
- • Maschinenkonstruktion
💻 Computergrafik
- • Polygon-Modellierung
- • Mesh-Generierung
- • Textur-Mapping
- • 3D-Modellierung
Mathematische Verallgemeinerungen
Ptolemäus-Ungleichung:
Für jedes Viereck gilt: $ef \leq ac + bd$
Gleichheit tritt nur bei Sehnenvierecken auf.
Varignon-Theorem:
Die Mittelpunkte der Seiten eines beliebigen Vierecks bilden ein Parallelogramm.
Die Fläche dieses Parallelogramms ist halb so groß wie die des ursprünglichen Vierecks.
Gauss-Newton-Linie:
Bei einem vollständigen Viereck (mit Diagonalenschnittpunkt) gibt es besondere Beziehungen zwischen den Mittelpunkten.
Euler-Linie des Vierecks:
Verallgemeinerung der Euler-Linie für Vierecke durch Schwerpunkt und Umkreismittelpunkt.
🌟 Das allgemeine Viereck - Universelle Geometrie:
- Universell: Umfasst alle Vierecktypen als Spezialfälle
- Flexibel: Berechnung mit minimalen Eingabeparametern
- Praktisch: Von Architektur bis Computergrafik anwendbar
- Mathematisch: Grundlage für komplexere geometrische Strukturen
KreisDreiecke
DreieckSpezielle Vierecke
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)
QuadratPolygone
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt
N-Eck (Universal)Allgemeine Vierecke
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)
Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)