Vieleckring Rechner
Online Rechner für regelmäßige Polygon-Ringe (Annuli)
Geben Sie die Anzahl der Ecken und mindestens zwei weitere Werte ein. Der Rechner berechnet automatisch alle anderen Eigenschaften des regelmäßigen Vieleckrings.
Eingabeformat
Anzahl der Ecken: 3 bis 100. Die äußere Seitenlänge muss größer als die innere sein. Dezimalzahlen können mit Punkt oder Komma eingegeben werden.
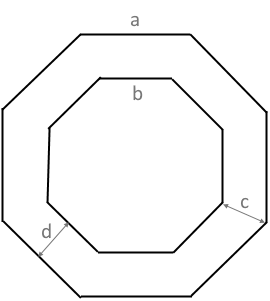
Der regelmäßige Vieleckring (Polygonaler Annulus)
Ein regelmäßiger Vieleckring ist ein Ring zwischen zwei konzentrischen regelmäßigen Polygonen mit gleicher Eckenzahl. Diese Geometrie wird auch als polygonaler Annulus bezeichnet und findet Anwendung in Technik, Architektur und Materialwissenschaft.
🔶 Ring-Eigenschaften
- • Äußeres Polygon mit Seitenlänge a
- • Inneres Polygon mit Seitenlänge b < a
- • Konzentrische Anordnung
- • Gleiche Eckenzahl n für beide Polygone
📏 Dicken-Konzept
Zwei verschiedene Dicken:
c > d (Ecken > Seiten)
Grundlegende Formeln
📊 Alle Berechnungen basieren auf äußerer (a) und innerer (b) Seitenlänge:
Ring-Fläche:
$$A_{Ring} = \frac{n}{4} \cot\left(\frac{\pi}{n}\right) \times (a^2 - b^2)$$
Gesamt-Umfang:
$$U_{gesamt} = n \times (a + b)$$
Dicke an Ecken:
$$c = \frac{a - b}{2 \sin(\pi/n)}$$
Dicke an Seiten:
$$d = \frac{a - b}{2 \tan(\pi/n)}$$
Verhältnis der Dicken:
$$\frac{c}{d} = \frac{1}{\sin(\pi/n) \cdot \tan(\pi/n)} = \frac{1}{\sin^2(\pi/n)} \cdot \cos(\pi/n)$$
Praktische Beispiele
📝 Beispielrechnung: Oktagon-Ring
Gegeben: n = 8, äußere Seitenlänge a = 5 cm, innere Seitenlänge b = 3 cm
Ring-Fläche berechnen:
$A = \frac{8}{4} \cot\left(\frac{\pi}{8}\right) \times (25 - 9) = 2 \times 2{,}414 \times 16 \approx 77{,}25$ cm²
Gesamt-Umfang berechnen:
$U = 8 \times (5 + 3) = 8 \times 8 = 64$ cm
Dicke an Ecken berechnen:
$c = \frac{5 - 3}{2 \sin(\pi/8)} = \frac{2}{2 \times 0{,}383} \approx 2{,}61$ cm
Dicke an Seiten berechnen:
$d = \frac{5 - 3}{2 \tan(\pi/8)} = \frac{2}{2 \times 0{,}414} \approx 2{,}41$ cm
Verhältnis prüfen:
$\frac{c}{d} = \frac{2{,}61}{2{,}41} \approx 1{,}08$ (c > d ✓)
Geometrische Analyse
Der Vieleckring zeigt eine wichtige geometrische Eigenschaft: Die Dicke ist nicht konstant um den Ring herum.
Dicken-Variation:
• Maximale Dicke c tritt an den Ecken auf
• Minimale Dicke d tritt in der Mitte der Seiten auf
• Das Verhältnis c/d hängt nur von der Eckenzahl n ab
Beziehung zu trigonometrischen Funktionen:
$$\frac{c}{d} = \frac{\tan(\pi/n)}{\sin(\pi/n)} = \frac{1}{\cos(\pi/n)}$$
Für große n (viele Ecken) nähert sich c/d dem Wert 1, da das Polygon einem Kreis ähnelt.
Rückrechnungsformeln
🔄 Umkehrformeln für verschiedene Eingabeparameter
Aus Ring-Fläche und äußerer Seitenlänge:
$$b = \sqrt{a^2 - \frac{4A \tan(\pi/n)}{n}}$$
Aus Ring-Fläche und innerer Seitenlänge:
$$a = \sqrt{b^2 + \frac{4A \tan(\pi/n)}{n}}$$
Aus Dicke an Ecken:
$$a = b + 2c \sin(\pi/n)$$
Aus Dicke an Seiten:
$$a = b + 2d \tan(\pi/n)$$
Spezialfälle und Grenzwerte
🔍 Mathematische Grenzfälle
Grenzfall n → ∞ (Kreisring):
$$\lim_{n \to \infty} A_{Ring} = \pi \left(\frac{a}{2\sin(\pi/n)}\right)^2 - \pi \left(\frac{b}{2\sin(\pi/n)}\right)^2$$ $$= \pi(R_a^2 - R_i^2) \text{ mit } R_a,R_i \text{ als Kreisradien}$$
Dreieck-Ring (n = 3):
$$A = \frac{\sqrt{3}}{4}(a^2 - b^2), \quad c = \frac{a-b}{2\sin(60°)} = \frac{a-b}{\sqrt{3}}$$
Quadrat-Ring (n = 4):
$$A = a^2 - b^2, \quad c = d = \frac{a-b}{\sqrt{2}}$$
Praktische Anwendungen
🏗️ Maschinenbau & Technik
- • Dichtungsringe mit polygonaler Form
- • Rohrleitungen mit eckigem Querschnitt
- • Werkzeugaufnahmen
- • Stanzwerkzeuge
🏛️ Architektur & Design
- • Polygonale Säulenquerschnitte
- • Dekorative Rahmen
- • Strukturelle Hohlprofile
- • Ornamente und Muster
🔬 Materialwissenschaft
- • Hohlkörper-Berechnung
- • Materialersparnis-Analyse
- • Gewichts-Optimierung
- • Festigkeits-Berechnungen
🎨 Geometrische Kunst
- • Muster und Ornamente
- • Symmetrische Designs
- • Fraktale Strukturen
- • Tessellations
🌟 Wichtige Eigenschaften des Vieleckrings:
- Variable Dicke: c (an Ecken) > d (an Seiten) für alle n
- Konzentrisch: Beide Polygone haben denselben Mittelpunkt
- Skalierbar: Verhältnisse bleiben bei Größenänderung erhalten
- Annulus-Geometrie: Spezialfall der Ring-Geometrie für Polygone
KreisDreiecke
DreieckSpezielle Vierecke
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)
QuadratPolygone
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt
N-Eck (Universal)Allgemeine Vierecke
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)
Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)