N-Eck Rechner
Online Rechner für regelmäßige Polygone mit n Seiten
Geben Sie die Anzahl der Ecken und einen weiteren Wert ein. Der Rechner berechnet automatisch alle anderen Eigenschaften des regelmäßigen n-Ecks.
Eingabeformat
Anzahl der Ecken: 3 bis 100. Dezimalzahlen können mit Punkt oder Komma eingegeben werden. Geben Sie nur einen weiteren Wert ein - alle anderen werden berechnet.
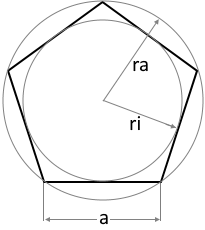
Das regelmäßige N-Eck (Allgemeines Polygon)
Ein regelmäßiges n-Eck ist ein Polygon mit n gleichen Seiten und n gleichen Innenwinkeln. Dieser universelle Rechner kann für jede Anzahl von Seiten von 3 (Dreieck) bis 100 verwendet werden und ermöglicht die Berechnung aller geometrischen Eigenschaften.
🔷 Universelle Eigenschaften
- • n gleiche Seiten der Länge a
- • n gleiche Innenwinkel
- • n Symmetrieachsen
- • n-zählige Rotationssymmetrie
⚙️ Konstruierbarkeit
Abhängig von n:
Gauß-Wantzel-Theorem
Allgemeine Formeln
📊 Alle Berechnungen basieren auf der Seitenlänge a und Eckenzahl n:
Innenwinkel:
$$\alpha = \frac{(n-2) \times 180°}{n}$$
Außenwinkel:
$$\beta = \frac{360°}{n}$$
Fläche:
$$A = \frac{n}{4} \cot\left(\frac{\pi}{n}\right) \times a^2$$
Umfang:
$$U = n \times a$$
Inkreisradius:
$$r = \frac{1}{2} \cot\left(\frac{\pi}{n}\right) \times a$$
Umkreisradius:
$$R = \frac{1}{2\sin(\pi/n)} \times a$$
Diagonalen (gesamt):
$$d_{gesamt} = \frac{n(n-3)}{2}$$
Praktische Beispiele
📝 Beispielrechnung: 8-Eck (Oktagon)
Gegeben: n = 8, Seitenlänge a = 5 cm
Innenwinkel berechnen:
$\alpha = \frac{(8-2) \times 180°}{8} = \frac{6 \times 180°}{8} = 135°$
Fläche berechnen:
$A = \frac{8}{4} \cot\left(\frac{\pi}{8}\right) \times 25 = 2 \times 2{,}414 \times 25 \approx 120{,}71$ cm²
Umfang berechnen:
$U = 8 \times 5 = 40$ cm
Inkreisradius berechnen:
$r = \frac{1}{2} \cot\left(\frac{\pi}{8}\right) \times 5 = 0{,}5 \times 2{,}414 \times 5 \approx 6{,}04$ cm
Umkreisradius berechnen:
$R = \frac{5}{2\sin(\pi/8)} = \frac{5}{2 \times 0{,}383} \approx 6{,}53$ cm
Konstruierbarkeit nach Gauß-Wantzel
Ein regelmäßiges n-Eck ist genau dann mit Zirkel und Lineal konstruierbar, wenn:
$$n = 2^k \times p_1 \times p_2 \times \ldots \times p_s$$
wobei k ≥ 0 und die $p_i$ verschiedene Fermat-Primzahlen sind.
Bekannte Fermat-Primzahlen:
$F_0 = 3$, $F_1 = 5$, $F_2 = 17$, $F_3 = 257$, $F_4 = 65537$
Konstruierbare n-Ecke (kleine n):
3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, ...
Nicht konstruierbare n-Ecke:
7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 26, 27, 28, 29, 31, 33, 35, 36, 37, 38, 39, ...
Spezialfall-Tabelle
| n | Name | Innenwinkel | Konstruierbar | Besonderheit |
|---|---|---|---|---|
| 3 | Dreieck | 60° | ✓ | Einfachstes Polygon |
| 4 | Quadrat | 90° | ✓ | Rechte Winkel |
| 5 | Pentagon | 108° | ✓ | Goldener Schnitt |
| 6 | Hexagon | 120° | ✓ | Bienenwaben |
| 7 | Heptagon | 128,57° | ✗ | Erste nicht konstruierbare |
| 8 | Oktagon | 135° | ✓ | Stoppschild-Form |
| 10 | Dekagon | 144° | ✓ | Pentagon × 2 |
| 12 | Dodekagon | 150° | ✓ | Uhren-Zifferblatt |
Praktische Anwendungen
🏛️ Architektur & Design
- • Kuppeln und Gewölbe
- • Grundrisse von Gebäuden
- • Dekorative Elemente
- • Parkettierung und Muster
🔬 Wissenschaft & Technik
- • Kristallstrukturen
- • Maschinenbau-Komponenten
- • Optische Instrumente
- • Computergrafik-Algorithmen
🌟 Universeller N-Eck Rechner:
- Flexibilität: Alle regelmäßigen Polygone von 3 bis 100 Ecken
- Präzision: Exakte trigonometrische Berechnungen
- Konstruierbarkeit: Automatische Überprüfung nach Gauß-Wantzel-Theorem
- Bildung: Ideal zum Verstehen von Polygon-Eigenschaften
KreisDreiecke
DreieckSpezielle Vierecke
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)
QuadratPolygone
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt
N-Eck (Universal)Allgemeine Vierecke
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)
Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)