Hendekagon Rechner
Online Rechner für regelmäßige Elfecke
Geben Sie einen bekannten Wert ein. Der Rechner berechnet automatisch alle anderen Eigenschaften des regelmäßigen Elfecks (Hendekagon).
Eingabeformat
Dezimalzahlen können mit Punkt oder Komma eingegeben werden. Geben Sie nur einen Wert ein - alle anderen werden berechnet.
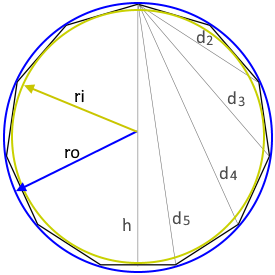
Das Hendekagon (Regelmäßiges Elfeck)
Ein Hendekagon ist ein regelmäßiges Elfeck mit elf gleichen Seiten und elf gleichen Innenwinkeln. Es ist ein besonderes Polygon, da 11 eine Primzahl ist und daher nicht mit Zirkel und Lineal konstruierbar ist.
1️⃣1️⃣ Grundeigenschaften
- • 11 gleiche Seiten der Länge a
- • 11 gleiche Innenwinkel von ≈ 147,27°
- • 11 Symmetrieachsen
- • 11-zählige Rotationssymmetrie
⚠️ Nicht konstruierbar
Mathematische Eigenschaft:
11 ist Primzahl
Grundlegende Formeln
📊 Alle Berechnungen basieren auf der Seitenlänge a:
Innenwinkel:
$$\alpha = \frac{(11-2) \times 180°}{11} = \frac{1620°}{11} \approx 147{,}27°$$
Diagonalen (trigonometrisch):
$$d_k = 2R \sin\left(\frac{k\pi}{11}\right) \text{ für } k = 2, 3, 4, 5$$
Fläche:
$$A = \frac{11a^2}{4 \tan(\pi/11)} \approx 9{,}366 \times a^2$$
Umfang:
$$U = 11a$$
Inkreisradius:
$$r = \frac{a}{2 \tan(\pi/11)} \approx 1{,}703 \times a$$
Umkreisradius:
$$R = \frac{a}{2 \sin(\pi/11)} \approx 1{,}775 \times a$$
Praktische Beispiele
📝 Beispielrechnung
Gegeben: Seitenlänge a = 5 cm
Innenwinkel berechnen:
$\alpha = \frac{9 \times 180°}{11} = \frac{1620°}{11} \approx 147{,}27°$
Fläche berechnen:
$A = 9{,}366 \times a^2 = 9{,}366 \times 25 \approx 234{,}15$ cm²
Umfang berechnen:
$U = 11 \times a = 11 \times 5 = 55$ cm
Inkreisradius berechnen:
$r = 1{,}703 \times a = 1{,}703 \times 5 \approx 8{,}52$ cm
Umkreisradius berechnen:
$R = 1{,}775 \times a = 1{,}775 \times 5 \approx 8{,}88$ cm
Konstruierbarkeit und Approximation
Das regelmäßige Hendekagon ist nicht mit Zirkel und Lineal konstruierbar, da 11 eine Primzahl ist.
Näherungskonstruktionen:
- Winkelteilung: Teilung von 360° in 11 gleiche Teile (≈ 32,73°)
- Trigonometrische Berechnung: Verwendung von sin(π/11) und cos(π/11)
- Iterative Verfahren: Numerische Näherung
- Computer-gestützte Konstruktion: CAD-Programme
Praktische Anwendungen
🎨 Kunst & Design
- • Spezielle Ornamente
- • Mandala-Designs
- • Abstrakte Kunst
- • Digitale Muster
🔬 Wissenschaft & Technik
- • Kristallstruktur-Studien
- • Robotik-Sensoren
- • Optische Anwendungen
- • Mathematische Forschung
1️⃣1️⃣ Besondere Eigenschaften:
- Primzahl: 11 ist eine Primzahl, daher nicht konstruierbar
- 11-zählige Symmetrie: Rotation um ≈ 32,73° führt zur deckungsgleichen Figur
- Seltene Verwendung: Hauptsächlich in spezieller Mathematik und Kunst
- Annäherung: Nur durch numerische Verfahren exakt darstellbar
KreisDreiecke
DreieckSpezielle Vierecke
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)
QuadratPolygone
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt
N-Eck (Universal)Allgemeine Vierecke
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)
Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)