Hexadekagon Rechner
Online Rechner für regelmäßige 16-Ecke
Geben Sie einen bekannten Wert ein. Der Rechner berechnet automatisch alle anderen Eigenschaften des regelmäßigen 16-Ecks (Hexadekagon).
Eingabeformat
Dezimalzahlen können mit Punkt oder Komma eingegeben werden. Geben Sie nur einen Wert ein - alle anderen werden berechnet.
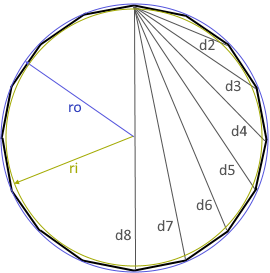
Das Hexadekagon (Regelmäßiges 16-Eck)
Ein Hexadekagon ist ein regelmäßiges 16-Eck mit sechzehn gleichen Seiten und sechzehn gleichen Innenwinkeln. Es ist konstruierbar, da 16 = 2⁴ ist, und verfügt über bemerkenswerte Symmetrieeigenschaften mit 7 verschiedenen Diagonalenlängen.
🟠 Grundeigenschaften
- • 16 gleiche Seiten der Länge a
- • 16 gleiche Innenwinkel von 157,5°
- • 16 Symmetrieachsen
- • 16-zählige Rotationssymmetrie
🌟 Konstruierbarkeit
Besondere Eigenschaft:
16 = 2⁴ (reine Zweierpotenz)
Grundlegende Formeln
📊 Alle Berechnungen basieren auf der Seitenlänge a:
Innenwinkel:
$$\alpha = \frac{(16-2) \times 180°}{16} = 157{,}5°$$
Diagonalen (dk für k=2..8):
$$d_k = \frac{\sin(k \times \pi/16)}{\sin(\pi/16)} \times a$$
Durchmesser (d8):
$$d_8 = \frac{a}{\sin(\pi/16)} \approx 5{,}126 \times a$$
Fläche:
$$A = 4 \cot(\pi/16) \times a^2 \approx 20{,}109 \times a^2$$
Umfang:
$$U = 16a$$
Inkreisradius:
$$r = \frac{1}{2} \cot(\pi/16) \times a \approx 2{,}514 \times a$$
Umkreisradius:
$$R = \frac{1}{2\sin(\pi/16)} \times a \approx 2{,}563 \times a$$
Praktische Beispiele
📝 Beispielrechnung
Gegeben: Seitenlänge a = 5 cm
Erste Diagonale berechnen:
$d_2 = 1{,}961 \times a = 1{,}961 \times 5 \approx 9{,}81$ cm
Durchmesser berechnen:
$d_8 = 5{,}126 \times a = 5{,}126 \times 5 \approx 25{,}63$ cm
Fläche berechnen:
$A = 20{,}109 \times a^2 = 20{,}109 \times 25 \approx 502{,}73$ cm²
Umfang berechnen:
$U = 16 \times a = 16 \times 5 = 80$ cm
Inkreisradius berechnen:
$r = 2{,}514 \times a = 2{,}514 \times 5 \approx 12{,}57$ cm
Umkreisradius berechnen:
$R = 2{,}563 \times a = 2{,}563 \times 5 \approx 12{,}82$ cm
Konstruierbarkeit und mathematische Eigenschaften
Das regelmäßige Hexadekagon ist vollständig konstruierbar, da 16 = 2⁴ eine reine Zweierpotenz ist.
Konstruktionsverfahren:
- Aus dem Oktagon: Halbierung aller Zentralwinkel (22,5° → 11,25°)
- Aus dem Quadrat: Vierteilung aller Zentralwinkel (90° → 22,5° → 11,25°)
- Direkte Konstruktion: Kreisteilung in 16 gleiche Teile
- 7 verschiedene Diagonalen: d₂, d₃, d₄, d₅, d₆, d₇, d₈
- Symmetrie: 16 Symmetrieachsen, sehr hohe Rotationssymmetrie
- Trigonometrie: Alle Werte basieren auf sin(π/16) und cos(π/16)
- Konstruierbarkeit: Exakte Konstruktion mit Zirkel und Lineal möglich
Praktische Anwendungen
🏛️ Architektur & Design
- • Seltene Kuppelformen
- • Dekorative Grundrisse
- • Spezielle Fensterformen
- • Pavillon-Design
🔧 Technik & Wissenschaft
- • Präzisions-Maschinenbau
- • Optische Instrumente
- • Mathematische Studien
- • CAD-Design
🌟 Besondere Eigenschaften des Hexadekagons:
- Konstruierbar: 16 = 2⁴, vollständig mit Zirkel und Lineal konstruierbar
- 7 Diagonalen: Alle mit exakten trigonometrischen Werten berechenbar
- Hohe Symmetrie: 16 Symmetrieachsen, sehr gleichmäßige Form
- Mathematische Bedeutung: Wichtig für Studien regulärer Polygone
KreisDreiecke
DreieckSpezielle Vierecke
Gleichseitiges Dreieck
Gleichschenkliges Dreieck
Rechtwinkliges Dreieck
Seitenhalbierende
Dreieck (Koordinaten)
QuadratPolygone
Rechteck
Parallelogramm
Raute
Symmetrisches Trapez
Rechtwinkliges Trapez
Dreigleichseitiges Trapez
Trapez Diagonale p
Trapez Diagonale q
Goldene-Rechteck
Rechteck in Quadrat
Rahmen (rechteckig)
Konkaves Viereck
Pfeilviereck
Drachenviereck
Drachenviereck Flächeninhalt
N-Eck (Universal)Allgemeine Vierecke
Vieleckring
Pentagon (Fünfeck)
Hexagon (Sechseck)
Konkaves Hexagon
Heptagon (Siebeneck)
Oktagon (Achteck)
Nonagon (Neuneck)
Dekagon (Zehneck)
Hendekagon (Elfeck)
Dodekagon (Zwölfeck)
Hexadekagon (16-eck)
Sehnenviereck
Überschlagenes Viereck
Unregelmäßiges Viereck
Viereck (Koordinaten)