Inverser hyperbolischer Tangens (atanh) Rechner
Berechnung des Winkels zum hyperbolischen Tangens mit mathematischen Eigenschaften
Geben Sie den hyperbolischen Tangenswert ein (zwischen -1 und 1) und klicken Sie auf Berechnen um den entsprechenden Winkel zu ermitteln. Der inverse hyperbolische Tangens ist die Umkehrfunktion von tanh.
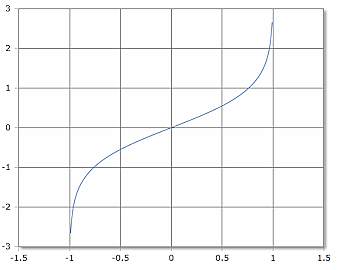
Graphische Darstellung der atanh-Funktion
Umkehrfunktion des hyperbolischen Tangens
Inverser hyperbolischer Tangens verstehen
Der inverse hyperbolische Tangens (atanh) ist die Umkehrfunktion des hyperbolischen Tangens. Er berechnet den Winkel α, für den tanh(α) = x gilt. Diese Funktion ist nur für -1 < x < 1 definiert und hat Singularitäten bei \(x = \pm 1\).
📐 Definition
Umkehrfunktion von tanh:
⚠️ Kritische Eigenschaften
- • Definitionsbereich: \((-1, 1)\)
- • Wertebereich: \((-\infty, \infty)\)
- • Singularitäten bei \(x = \pm 1\)
- • Ungerade Funktion: \(\text{atanh}(-x) = -\text{atanh}(x)\)
🔬 Anwendungen
- • Geschwindigkeitsaddition (Relativitätstheorie)
- • Logistische Regression
- • Fisher-Transformation
- • Hyperbolic Geometry
⭐ Spezielle Werte
- • \(\text{atanh}(0) = 0\)
- • \(\text{atanh}(0{,}5) \approx 0{,}549\)
- • \(\text{atanh}(-0{,}5) \approx -0{,}549\)
- • \(\lim_{x \to 1^-} \text{atanh}(x) = +\infty\)
Mathematische Eigenschaften
📐 Grundformel
Definition des inversen hyperbolischen Tangens:
\[\text{atanh}(x) = \frac{1}{2}\ln\left(\frac{1+x}{1-x}\right)\] \[\text{für } x \in (-1, 1)\]
Herleitung: Aus \(y = \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}\) folgt \(x = \text{atanh}(y)\)
🔄 Beziehungen zu anderen Funktionen
Zusammenhänge mit verwandten Funktionen:
\[\tanh(\text{atanh}(x)) = x \text{ für } x \in (-1, 1)\] \[\text{atanh}(\tanh(x)) = x \text{ für alle } x \in \mathbb{R}\] \[\text{atanh}(x) = -\text{atanh}(-x) \text{ (ungerade Funktion)}\] \[\text{atanh}(x) = \frac{1}{2}\text{asinh}\left(\frac{2x}{1-x^2}\right) \text{ für } |x| < 1\]
📊 Ableitung und Integration
Differential- und Integralrechnung:
\[\frac{d}{dx}\text{atanh}(x) = \frac{1}{1-x^2} \text{ für } |x| < 1\] \[\int \text{atanh}(x) \, dx = x \cdot \text{atanh}(x) + \frac{1}{2}\ln(1-x^2) + C\] \[\int \frac{1}{1-x^2} \, dx = \text{atanh}(x) + C \text{ für } |x| < 1\]
Beachte: Die Ableitung hat Pole bei \(x = \pm 1\)
Singularitäten und Grenzverhalten
⚠️ Kritisches Verhalten bei den Rändern
Verhalten nahe den Singularitäten:
\[\lim_{x \to 1^-} \text{atanh}(x) = +\infty\] \[\lim_{x \to -1^+} \text{atanh}(x) = -\infty\] \[\text{Für } x \to 1^-: \text{atanh}(x) \sim -\frac{1}{2}\ln(1-x)\] \[\text{Für } x \to 0: \text{atanh}(x) \sim x\]
Wichtig: Bei \(x = \pm 1\) ist die Funktion nicht definiert
Praktische Berechnungsbeispiele
📝 Beispiel 1: Grundwerte berechnen
Aufgabe: Berechnung verschiedener atanh-Werte
Berechnung:
\[\text{atanh}(0) = \frac{1}{2}\ln\left(\frac{1+0}{1-0}\right) = \frac{1}{2}\ln(1) = 0\] \[\text{atanh}(0{,}5) = \frac{1}{2}\ln\left(\frac{1{,}5}{0{,}5}\right) = \frac{1}{2}\ln(3) \approx 0{,}549\] \[\text{atanh}(-0{,}5) = \frac{1}{2}\ln\left(\frac{0{,}5}{1{,}5}\right) = \frac{1}{2}\ln\left(\frac{1}{3}\right) \approx -0{,}549\]
Verifikation: \(\tanh(0{,}549) \approx 0{,}5\) ✓, ungerade Funktion ✓
📝 Beispiel 2: Relativistische Geschwindigkeitsaddition
Aufgabe: Rapidität in der speziellen Relativitätstheorie
Gegeben: Geschwindigkeit \(v = 0{,}8c\)
Berechnung:
\[\text{Rapidität: } \phi = \text{atanh}\left(\frac{v}{c}\right)\] \[\phi = \text{atanh}(0{,}8) = \frac{1}{2}\ln\left(\frac{1{,}8}{0{,}2}\right) = \frac{1}{2}\ln(9) \approx 1{,}099\] \[\text{Verifikation: } v = c \cdot \tanh(\phi) = c \cdot \tanh(1{,}099) \approx 0{,}8c\]
Physik: Rapiditäten addieren sich linear: \(\phi_{ges} = \phi_1 + \phi_2\)
📝 Beispiel 3: Fisher-Transformation
Aufgabe: Transformation des Korrelationskoeffizienten
Gegeben: Korrelation \(r = 0{,}6\)
Berechnung:
\[\text{Fisher-z: } z = \text{atanh}(r) = \text{atanh}(0{,}6)\] \[z = \frac{1}{2}\ln\left(\frac{1{,}6}{0{,}4}\right) = \frac{1}{2}\ln(4) \approx 0{,}693\] \[\text{Standardfehler: } SE_z = \frac{1}{\sqrt{n-3}} \text{ (für große Stichproben)}\]
Statistik: Fisher-z ist approximativ normalverteilt
Numerische und geometrische Eigenschaften
📊 Asymptotisches Verhalten
- • Für \(x \to 1^-\): \(\text{atanh}(x) \to +\infty\)
- • Für \(x \to -1^+\): \(\text{atanh}(x) \to -\infty\)
- • Für \(x \to 0\): \(\text{atanh}(x) \sim x\)
- • Vertikale Asymptoten bei \(x = \pm 1\)
🔢 Reihenentwicklung
- • Für \(|x| < 1\):
- • \(\text{atanh}(x) = x + \frac{x^3}{3} + \frac{x^5}{5} + \frac{x^7}{7} + \ldots\)
- • \(\text{atanh}(x) = \sum_{n=0}^{\infty} \frac{x^{2n+1}}{2n+1}\)
- • Konvergenzradius: \(R = 1\)
Vergleich der hyperbolischen Umkehrfunktionen
asinh(x)
Inverser hyperbolischer Sinus
Def: \(\mathbb{R} \to \mathbb{R}\)
\(\text{asinh}(x) = \ln(x + \sqrt{x^2+1})\)
Universell definiert
acosh(x)
Inverser hyperbolischer Kosinus
Def: \([1,\infty) \to [0,\infty)\)
\(\text{acosh}(x) = \ln(x + \sqrt{x^2-1})\)
Halbseitig beschränkt
atanh(x)
Inverser hyperbolischer Tangens
Def: \((-1,1) \to \mathbb{R}\)
\(\text{atanh}(x) = \frac{1}{2}\ln\left(\frac{1+x}{1-x}\right)\)
Mit Singularitäten
Anwendungen in Physik und Mathematik
🚀 Relativitätstheorie
Geschwindigkeitsaddition und Rapidität:
\[\text{Rapidität: } \phi = \text{atanh}\left(\frac{v}{c}\right)\] \[\text{Geschwindigkeitsaddition: } v_{12} = \frac{v_1 + v_2}{1 + \frac{v_1 v_2}{c^2}}\] \[\text{Rapiditäten addieren sich linear: } \phi_{12} = \phi_1 + \phi_2\]
Vorteil: Linearität der Rapiditäten vereinfacht Berechnungen
📊 Statistik und Data Science
Fisher-Transformation und Logit-Funktion:
\[\text{Fisher-z: } z = \text{atanh}(r) \text{ für Korrelation } r\] \[\text{Logit: } \text{logit}(p) = \ln\left(\frac{p}{1-p}\right) = 2 \cdot \text{atanh}(2p-1)\] \[\text{Standardfehler: } SE_z = \frac{1}{\sqrt{n-3}}\]
Anwendung: Konfidenzintervalle für Korrelationskoeffizienten
⚠️ Wichtige Warnung bei atanh-Berechnungen:
- Definitionsbereich beachten: Nur für \(-1 < x < 1\) definiert
- Singularitäten vermeiden: Bei \(x = \pm 1\) entstehen unendliche Werte
- Numerische Stabilität: Für \(|x|\) nahe 1 alternative Formeln verwenden
- Physikalische Bedeutung: In der Relativitätstheorie entspricht \(|x| = 1\) Lichtgeschwindigkeit
🔬 Anwendungsgebiete der atanh-Funktion:
- Relativitätstheorie: Rapidität und Geschwindigkeitsaddition
- Statistik: Fisher-Transformation von Korrelationskoeffizienten
- Machine Learning: Logit-Funktion und logistische Regression
- Hyperbolische Geometrie: Poincaré-Modell und Distanzmessungen
Vollständige Taylor-Reihenentwicklung
🔢 Taylor-Reihe von atanh(x)
Vollständige Reihenentwicklung um \(x = 0\):
\[\text{atanh}(x) = \sum_{n=0}^{\infty} \frac{x^{2n+1}}{2n+1} = x + \frac{x^3}{3} + \frac{x^5}{5} + \frac{x^7}{7} + \frac{x^9}{9} + \ldots\] \[\text{Konvergenzradius: } R = 1\] \[\text{Konvergenzintervall: } (-1, 1)\]
Beachte: Die Reihe konvergiert nur für \(|x| < 1\) und divergiert an den Rändern \(x = \pm 1\)
Praktische Integralformeln mit atanh
| Integral | Stammfunktion | Gültigkeitsbereich |
|---|---|---|
| \(\int \frac{1}{1-x^2} dx\) | \(\text{atanh}(x) + C\) | \(|x| < 1\) |
| \(\int \frac{1}{a^2-x^2} dx\) | \(\frac{1}{a}\text{atanh}\left(\frac{x}{a}\right) + C\) | \(|x| < a\) |
| \(\int \text{atanh}(x) dx\) | \(x \cdot \text{atanh}(x) + \frac{1}{2}\ln(1-x^2) + C\) | \(|x| < 1\) |
| \(\int \frac{x}{\sqrt{1-x^2}} dx\) | \(-\sqrt{1-x^2} + C\) | \(|x| < 1\) |
acos - Arkuskosinus
acot - Arkuskotangens
acsc - Arkuskosekans
asec - Arkussekans
asin - Arkussinus
atan - Arkustangens
atan2 - Arkustangens von y/x
cos - Kosinus
cot - Kotangens
csc - Kosekans
sec - Sekans
sin - Sinus
sinc - Kardinalsinus
tan - Tangens
hypot - Hypotenuse
deg2rad - Grad in Radiant
rad2deg - Radiant in Grad
Hyperbolik
acosh - Arkuskosinus hyperbolikus
asinh - Areasinus hyperbolikus
atanh - Arkustangens hyperbolikus
cosh - Kosinus hyperbolikus
sinh - Sinus hyperbolikus
tanh - Tangens hyperbolikus
Logarithmus
log - Logarithmus zur angegebene Basis
ln - Natürlicher Logarithmus zur Basis e
log10 - Logarithmus zur Basis 10
log2 - Logarithmus zur Basis 2
exp - Exponenten zur Basis e
Aktivierung
Softmax
Sigmoid
Derivate Sigmoid
Logit
Derivate Logit
Softsign
Derivate Softsign
Softplus
Logistic
Gamma
Eulersche Gamma Funktion
Lanczos Gamma-Funktion
Stirling Gamma-Funktion
Log Gamma-Funktion
Beta
Beta Funktion
Logarithmische Beta Funktion
Unvollstaendige Beta Funktion
Inverse unvollstaendige Beta Funktion
Fehlerfunktionen
erf - Fehlerfunktion
erfc - komplementäre Fehlerfunktion
Kombinatorik
Fakultät
Semifakultät
Steigende Fakultät
Fallende Fakultät
Subfakultät
Permutationen und Kombinationen
Permutation
Kombinationen
Mittlerer Binomialkoeffizient
Catalan-Zahl
Lah Zahl