Arkuskotangens (acot) Rechner
Berechnung des Winkels zum gegebenen Kotangenswert mit mathematischen Eigenschaften
Geben Sie den Kotangenswert ein (beliebige reelle Zahl ≠ 0) und klicken Sie auf Berechnen um den entsprechenden Winkel zu ermitteln. Der Arkuskotangens ist die Umkehrfunktion von cot.
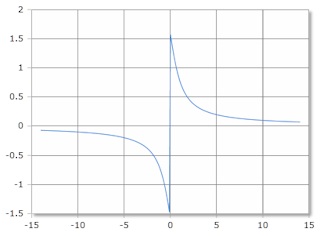
Graphische Darstellung der acot-Funktion
Arkuskotangens (Inverser Kotangens)
Arkuskotangens verstehen
Der Arkuskotangens (acot) ist die Umkehrfunktion des Kotangens. Er berechnet den Winkel α, für den cot(α) = x gilt. Diese Funktion ist für alle x ≠ 0 definiert und hat einen Wertebereich von (0, π) Radiant bzw. (0°, 180°).
📐 Definition
Umkehrfunktion von cot:
📊 Eigenschaften
- • Definitionsbereich: \(\mathbb{R} \setminus \{0\}\)
- • Wertebereich: \((0, \pi)\) rad
- • Wertebereich: \((0°, 180°)\)
- • Streng monoton fallend
🔬 Anwendungen
- • Geometrie und Trigonometrie
- • Physik (Optik, Mechanik)
- • Ingenieurswesen (Statik)
- • Computergrafik
⭐ Spezielle Werte
- • \(\text{acot}(1) = 45° = \frac{\pi}{4}\)
- • \(\text{acot}(\sqrt{3}) = 30° = \frac{\pi}{6}\)
- • \(\text{acot}(\frac{1}{\sqrt{3}}) = 60° = \frac{\pi}{3}\)
- • \(\lim_{x \to 0^+} \text{acot}(x) = \frac{\pi}{2}\)
Mathematische Eigenschaften
📐 Grundbeziehung
Definition des Arkuskotangens:
\[y = \text{acot}(x) \Leftrightarrow \cot(y) = x\] \[\text{für } x \neq 0 \text{ und } y \in (0, \pi)\]
Beziehung zu arctan: \(\text{acot}(x) = \arctan\left(\frac{1}{x}\right)\) für \(x > 0\)
🔄 Wichtige Beziehungen
Zusammenhänge mit anderen Funktionen:
\[\text{acot}(x) = \arctan\left(\frac{1}{x}\right) \text{ für } x > 0\] \[\text{acot}(x) = \pi + \arctan\left(\frac{1}{x}\right) \text{ für } x < 0\] \[\text{acot}(x) + \text{acot}\left(\frac{1}{x}\right) = \frac{\pi}{2} \text{ für } x > 0\] \[\cot(\text{acot}(x)) = x \text{ für alle } x \neq 0\]
📊 Ableitung und Integration
Differential- und Integralrechnung:
\[\frac{d}{dx}\text{acot}(x) = -\frac{1}{1+x^2} \text{ für } x \neq 0\] \[\int \text{acot}(x) \, dx = x \cdot \text{acot}(x) + \frac{1}{2}\ln(1+x^2) + C\] \[\int \frac{1}{1+x^2} \, dx = \arctan(x) + C = -\text{acot}(x) + \frac{\pi}{2} + C\]
Beachte: Die Ableitung ist immer negativ, acot ist streng monoton fallend
Praktische Berechnungsbeispiele
📝 Beispiel 1: Rechtwinkliges Dreieck
Aufgabe: Winkel aus Seitenverhältnissen berechnen
Gegeben: Ankathete \(b = 8\), Gegenkathete \(a = 6\)
Berechnung:
\[\cot(\alpha) = \frac{\text{Ankathete}}{\text{Gegenkathete}} = \frac{8}{6} = \frac{4}{3} \approx 1{,}333\] \[\alpha = \text{acot}(1{,}333) \approx 36{,}87°\] \[\text{In Radiant: } \alpha \approx 0{,}644 \text{ rad}\]
Verifikation: \(\cot(36{,}87°) = 1{,}333\) ✓
📝 Beispiel 2: Spezielle Winkel
Aufgabe: Bekannte Kotangenswerte und ihre Winkel
Berechnung:
\[\text{acot}(\sqrt{3}) = 30° = \frac{\pi}{6} \text{ rad}\] \[\text{acot}(1) = 45° = \frac{\pi}{4} \text{ rad}\] \[\text{acot}\left(\frac{1}{\sqrt{3}}\right) = 60° = \frac{\pi}{3} \text{ rad}\] \[\lim_{x \to 0^+} \text{acot}(x) = 90° = \frac{\pi}{2} \text{ rad}\] \[\lim_{x \to \infty} \text{acot}(x) = 0° = 0 \text{ rad}\]
Merkhilfe: Diese Werte sind die Komplemente der entsprechenden arctan-Werte
📝 Beispiel 3: Steigungswinkel berechnen
Aufgabe: Steigungswinkel einer Rampe
Gegeben: Steigung 1:8 (Höhe:Länge)
Berechnung:
\[\text{Steigung} = \frac{\text{Höhe}}{\text{Länge}} = \frac{1}{8} = 0{,}125\] \[\tan(\alpha) = 0{,}125 \Rightarrow \cot(\alpha) = \frac{1}{0{,}125} = 8\] \[\alpha = \text{acot}(8) = \arctan\left(\frac{1}{8}\right) \approx 7{,}13°\] \[\text{Steigungswinkel: } \alpha \approx 7{,}13° \text{ oder } 0{,}124 \text{ rad}\]
Anwendung: Straßenbau, Rampenplanung, Architektur
Numerische und geometrische Eigenschaften
📊 Funktionsverhalten
- • Streng monoton fallend
- • Stetig für alle \(x \neq 0\)
- • \(\lim_{x \to 0^+} \text{acot}(x) = \frac{\pi}{2}\)
- • \(\lim_{x \to +\infty} \text{acot}(x) = 0\)
🔢 Reihenentwicklung
- • Für \(|x| > 1\):
- • \(\text{acot}(x) = \frac{1}{x} - \frac{1}{3x^3} + \frac{1}{5x^5} - \ldots\)
- • Für \(|x| < 1\): über arctan-Reihe
- • Asymptotisches Verhalten
Vergleich der inversen trigonometrischen Funktionen
arctan(x)
Arkustangens
Def: \(\mathbb{R} \to (-\frac{\pi}{2}, \frac{\pi}{2})\)
\(\arctan(x) = \frac{\pi}{2} - \text{acot}(x)\)
Monoton steigend
acot(x)
Arkuskotangens
Def: \(\mathbb{R}\setminus\{0\} \to (0, \pi)\)
\(\text{acot}(x) = \arctan\left(\frac{1}{x}\right)\)
Monoton fallend
arcsin(x)
Arkussinus
Def: \([-1,1] \to [-\frac{\pi}{2}, \frac{\pi}{2}]\)
\(\arcsin(x) = \arctan\left(\frac{x}{\sqrt{1-x^2}}\right)\)
Beschränkt
Geometrische Interpretation
🔵 Kotangens und rechtwinkliges Dreieck
Geometrische Bedeutung im rechtwinkligen Dreieck:
\[\cot(\alpha) = \frac{\text{Ankathete}}{\text{Gegenkathete}} = \frac{b}{a}\] \[\text{Dann: } \alpha = \text{acot}\left(\frac{b}{a}\right)\] \[\text{Komplementärwinkel: } \beta = 90° - \alpha = \text{acot}\left(\frac{a}{b}\right)\] \[\text{Pythagoras: } c^2 = a^2 + b^2\]
Interpretation: acot gibt den Winkel für ein gegebenes Seitenverhältnis an
💡 Wichtige Eigenschaften der acot-Funktion:
- Definitionsbereich: \(\mathbb{R} \setminus \{0\}\) (alle reellen Zahlen außer 0)
- Wertebereich: \((0, \pi)\) rad bzw. \((0°, 180°)\)
- Monotonie: Streng monoton fallend
- Beziehung: Komplement zu arctan für positive Werte
🔬 Anwendungsgebiete der acot-Funktion:
- Geometrie: Winkelberechnung in rechtwinkligen Dreiecken
- Ingenieurswesen: Steigungswinkel, Neigungsanalyse
- Physik: Optik (Brechungsgesetze), Mechanik
- Architektur: Dachneigungen, Rampenplanung
Vollständige Reihenentwicklung
🔢 Reihenentwicklung von acot(x)
Asymptotische Entwicklung für große |x|:
\[\text{acot}(x) = \frac{1}{x} - \frac{1}{3x^3} + \frac{1}{5x^5} - \frac{1}{7x^7} + \ldots \text{ für } |x| > 1\] \[= \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)x^{2n+1}} \text{ für } |x| > 1\] \[\text{Für kleine Werte: über } \text{acot}(x) = \arctan\left(\frac{1}{x}\right)\]
Beachte: Verschiedene Reihen für verschiedene Bereiche von x
Praktische Integralformeln mit acot
| Integral | Stammfunktion | Gültigkeitsbereich |
|---|---|---|
| \(\int \text{acot}(x) dx\) | \(x \cdot \text{acot}(x) + \frac{1}{2}\ln(1+x^2) + C\) | \(x \neq 0\) |
| \(\int \frac{1}{1+x^2} dx\) | \(\arctan(x) + C\) | Alle \(x\) |
| \(\int x \cdot \text{acot}(x) dx\) | \(\frac{x^2+1}{2}\text{acot}(x) - \frac{x}{2} + C\) | \(x \neq 0\) |
| \(\int \frac{\text{acot}(x)}{1+x^2} dx\) | \(\frac{[\text{acot}(x)]^2}{2} + C\) | \(x \neq 0\) |
acos - Arkuskosinus
acot - Arkuskotangens
acsc - Arkuskosekans
asec - Arkussekans
asin - Arkussinus
atan - Arkustangens
atan2 - Arkustangens von y/x
cos - Kosinus
cot - Kotangens
csc - Kosekans
sec - Sekans
sin - Sinus
sinc - Kardinalsinus
tan - Tangens
hypot - Hypotenuse
deg2rad - Grad in Radiant
rad2deg - Radiant in Grad
Hyperbolik
acosh - Arkuskosinus hyperbolikus
asinh - Areasinus hyperbolikus
atanh - Arkustangens hyperbolikus
cosh - Kosinus hyperbolikus
sinh - Sinus hyperbolikus
tanh - Tangens hyperbolikus
Logarithmus
log - Logarithmus zur angegebene Basis
ln - Natürlicher Logarithmus zur Basis e
log10 - Logarithmus zur Basis 10
log2 - Logarithmus zur Basis 2
exp - Exponenten zur Basis e
Aktivierung
Softmax
Sigmoid
Derivate Sigmoid
Logit
Derivate Logit
Softsign
Derivate Softsign
Softplus
Logistic
Gamma
Eulersche Gamma Funktion
Lanczos Gamma-Funktion
Stirling Gamma-Funktion
Log Gamma-Funktion
Beta
Beta Funktion
Logarithmische Beta Funktion
Unvollstaendige Beta Funktion
Inverse unvollstaendige Beta Funktion
Fehlerfunktionen
erf - Fehlerfunktion
erfc - komplementäre Fehlerfunktion
Kombinatorik
Fakultät
Semifakultät
Steigende Fakultät
Fallende Fakultät
Subfakultät
Permutationen und Kombinationen
Permutation
Kombinationen
Mittlerer Binomialkoeffizient
Catalan-Zahl
Lah Zahl