Fehlerfunktion Erf Rechner
Online Berechnung der Error Function für Statistik und Physik
Geben Sie das Argument x ein und klicken Sie auf Berechnen um die Fehlerfunktion zu ermitteln. Die Fehlerfunktion erf(x) ist eine fundamentale mathematische Funktion in der Statistik, Physik und Wahrscheinlichkeitstheorie, die eng mit der Normalverteilung verknüpft ist.
💡 Fehlerfunktion
\(\text{erf}(x) = \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2} \, dt\)
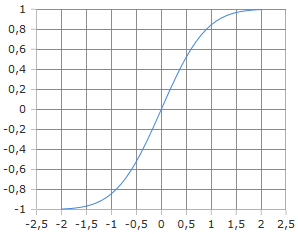
Charakteristische S-förmige Kurve der Fehlerfunktion
Die Fehlerfunktion verstehen
Die Fehlerfunktion (englisch: error function, abgekürzt als erf) ist eine spezielle mathematische Funktion, die vor allem in Statistik, Physik und Ingenieurwissenschaften verwendet wird. Sie ist eine Sigmoidfunktion mit einer charakteristischen S-förmigen Kurve und tritt häufig bei der Normalverteilung auf, wo sie die Wahrscheinlichkeit beschreibt, dass ein Wert innerhalb eines bestimmten Bereichs liegt.
📈 Definition
Mathematische Form:
📊 Eigenschaften
- • Ungerade Funktion: erf(-x) = -erf(x)
- • erf(0) = 0
- • erf(∞) = 1, erf(-∞) = -1
- • Wertebereich: [-1, 1]
- • Sigmoidaler Verlauf
🔬 Anwendungen
- • Normalverteilung CDF
- • Wärmeleitungsgleichung
- • Diffusionsprozesse
- • Quantenmechanik
⭐ Verwandte Funktionen
- • erfc(x) = 1 - erf(x)
- • erfi(x) = -i·erf(ix)
- • Φ(x) = ½[1 + erf(x/√2)]
- • dawson(x)
Mathematische Eigenschaften
📈 Grundlegende Eigenschaften
Wichtige mathematische Eigenschaften der Fehlerfunktion:
\[\text{Definition: } \text{erf}(x) = \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2} \, dt\] \[\text{Ungerade Funktion: } \text{erf}(-x) = -\text{erf}(x)\] \[\text{Grenzwerte: } \text{erf}(0) = 0, \quad \text{erf}(\infty) = 1, \quad \text{erf}(-\infty) = -1\] \[\text{Ableitung: } \frac{d}{dx}\text{erf}(x) = \frac{2}{\sqrt{\pi}} e^{-x^2}\] \[\text{Reihenentwicklung: } \text{erf}(x) = \frac{2}{\sqrt{\pi}} \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{n!(2n+1)}\]
🔄 Verbindung zur Normalverteilung
Zentrale Rolle in der Statistik:
\[\text{Standardnormalverteilung CDF: } \Phi(x) = \frac{1}{2}\left[1 + \text{erf}\left(\frac{x}{\sqrt{2}}\right)\right]\] \[\text{Allgemeine Normalverteilung: } F(x; \mu, \sigma) = \frac{1}{2}\left[1 + \text{erf}\left(\frac{x-\mu}{\sigma\sqrt{2}}\right)\right]\] \[\text{Wahrscheinlichkeit im Intervall: } P(a \leq X \leq b) = \frac{1}{2}\left[\text{erf}\left(\frac{b-\mu}{\sigma\sqrt{2}}\right) - \text{erf}\left(\frac{a-\mu}{\sigma\sqrt{2}}\right)\right]\] \[\text{2σ-Regel: } P(|\mu - X| \leq 2\sigma) = \text{erf}(\sqrt{2}) \approx 0{,}9545\]
📊 Wichtige Werte
Häufig verwendete Funktionswerte:
\[\text{erf}(0) = 0\] \[\text{erf}(0{,}5) \approx 0{,}5205\] \[\text{erf}(1) \approx 0{,}8427\] \[\text{erf}(\sqrt{2}) \approx 0{,}9545 \text{ (2σ-Bereich)}\] \[\text{erf}(2) \approx 0{,}9953\] \[\text{erf}(3) \approx 0{,}9999779\]
Praktische Anwendungsbeispiele
📝 Beispiel 1: Normalverteilung
Aufgabe: Wahrscheinlichkeit bei Standardnormalverteilung
Gegeben: X ~ N(0,1), gesucht P(X ≤ 1)
Berechnung:
\[P(X \leq 1) = \Phi(1) = \frac{1}{2}\left[1 + \text{erf}\left(\frac{1}{\sqrt{2}}\right)\right]\] \[\text{erf}\left(\frac{1}{\sqrt{2}}\right) = \text{erf}(0{,}7071) \approx 0{,}6827\] \[P(X \leq 1) = \frac{1}{2}[1 + 0{,}6827] = 0{,}8413\]
Interpretation: 84,13% der Werte liegen unter 1 bei der Standardnormalverteilung
📝 Beispiel 2: Wärmeleitung
Aufgabe: Temperaturverteilung in einem Stab
Szenario: Eindimensionale Wärmeleitung mit Anfangsbedingungen
Lösung:
\[\text{Wärmeleitungsgleichung: } \frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partial x^2}\] \[\text{Lösung mit Sprungfunktion: } u(x,t) = \frac{u_0}{2}\left[1 + \text{erf}\left(\frac{x}{2\sqrt{\alpha t}}\right)\right]\] \[\text{Für } x = 1, t = 1, \alpha = 0{,}1: u(1,1) = \frac{u_0}{2}\left[1 + \text{erf}\left(\frac{1}{2\sqrt{0{,}1}}\right)\right]\] \[= \frac{u_0}{2}[1 + \text{erf}(1{,}58)] \approx \frac{u_0}{2}[1 + 0{,}976] = 0{,}988 u_0\]
Anwendung: Temperaturverlauf in technischen Systemen
📝 Beispiel 3: Qualitätskontrolle
Aufgabe: Ausschussrate bei Fertigungsprozess
Gegeben: μ = 100mm, σ = 2mm, Toleranz: 96-104mm
Berechnung:
\[P(96 \leq X \leq 104) = P\left(\frac{96-100}{2} \leq Z \leq \frac{104-100}{2}\right)\] \[= P(-2 \leq Z \leq 2) = \Phi(2) - \Phi(-2)\] \[= \frac{1}{2}\left[\text{erf}\left(\frac{2}{\sqrt{2}}\right) - \text{erf}\left(\frac{-2}{\sqrt{2}}\right)\right]\] \[= \text{erf}(\sqrt{2}) = \text{erf}(1{,}414) \approx 0{,}9545\]
Bedeutung: 95,45% der Produkte liegen innerhalb der Toleranz (2σ-Regel)
Anwendungen in verschiedenen Bereichen
📊 Statistik
- • Normalverteilung CDF
- • Hypothesentests
- • Konfidenzintervalle
- • Qualitätskontrolle
🔬 Physik
- • Wärmeleitungsgleichung
- • Diffusionsprozesse
- • Quantenmechanik
- • Optik und Wellenlehre
⚙️ Ingenieurswesen
- • Signalverarbeitung
- • Regelungstechnik
- • Kommunikationstechnik
- • Zuverlässigkeitsanalyse
🧮 Numerische Mathematik
- • Spezielle Funktionen
- • Integralrechnung
- • Approximationstheorie
- • Monte-Carlo-Methoden
Implementierung und Code
💻 Code-Implementierungen
Effiziente Implementierung der Fehlerfunktion:
Python (SciPy/Math):
import math
from scipy.special import erf, erfc
import numpy as np
# Fehlerfunktion
result = math.erf(x) # Built-in seit Python 3.2
result = erf(x) # SciPy Version
# Anwendung: Normalverteilung CDF
def normal_cdf(x, mu=0, sigma=1):
"""Kumulative Verteilungsfunktion der Normalverteilung"""
return 0.5 * (1 + erf((x - mu) / (sigma * np.sqrt(2))))
# Beispiel: P(X ≤ 1) bei N(0,1)
prob = normal_cdf(1, 0, 1)
print(f"P(X ≤ 1) = {prob:.4f}")
R:
# R hat keine built-in erf, aber:
erf <- function(x) 2 * pnorm(x * sqrt(2)) - 1
# Oder mit speziellen Paketen:
library(pracma)
result <- erf(x)
MATLAB:
result = erf(x); % Built-in Funktion
% Normalverteilung CDF:
normal_cdf = @(x, mu, sigma) 0.5 * (1 + erf((x - mu) / (sigma * sqrt(2))));
🎯 Statistische Anwendung
Normalverteilungs-Toolkit:
Python Normalverteilungs-Toolkit:
import math
import numpy as np
class NormalDistribution:
def __init__(self, mu=0, sigma=1):
self.mu = mu
self.sigma = sigma
def cdf(self, x):
"""Kumulative Verteilungsfunktion"""
return 0.5 * (1 + math.erf((x - self.mu) / (self.sigma * math.sqrt(2))))
def pdf(self, x):
"""Wahrscheinlichkeitsdichtefunktion"""
return (1 / (self.sigma * math.sqrt(2 * math.pi))) * math.exp(-0.5 * ((x - self.mu) / self.sigma)**2)
def interval_prob(self, a, b):
"""P(a ≤ X ≤ b)"""
return self.cdf(b) - self.cdf(a)
def sigma_rule(self, k):
"""k-Sigma-Regel: P(|X - μ| ≤ k*σ)"""
return 2 * self.cdf(self.mu + k * self.sigma) - 1
# Beispiel
norm = NormalDistribution(100, 15)
print(f"2σ-Regel: {norm.sigma_rule(2):.4f}") # ≈ 0.9545
print(f"P(85 ≤ X ≤ 115): {norm.interval_prob(85, 115):.4f}")
🎯 Numerische Approximation
Eigene Implementierung für Lernzwecke:
Python Approximation:
import math
def erf_approx_series(x, terms=20):
"""Reihenentwicklung der Fehlerfunktion"""
if abs(x) > 3: # Für große x andere Methode verwenden
return math.copysign(1, x)
sum_term = 0
for n in range(terms):
numerator = ((-1)**n) * (x**(2*n + 1))
denominator = math.factorial(n) * (2*n + 1)
sum_term += numerator / denominator
return (2 / math.sqrt(math.pi)) * sum_term
def erf_approx_rational(x):
"""Rationale Approximation (Abramowitz & Stegun)"""
# Konstanten für die Approximation
a1, a2, a3, a4, a5 = 0.254829592, -0.284496736, 1.421413741, -1.453152027, 1.061405429
p = 0.3275911
# Für negative x nutzen wir die Ungerade-Eigenschaft
sign = 1 if x >= 0 else -1
x = abs(x)
# Approximationsformel
t = 1.0 / (1.0 + p * x)
y = 1.0 - (((((a5 * t + a4) * t) + a3) * t + a2) * t + a1) * t * math.exp(-x * x)
return sign * y
# Vergleich
x = 1.0
exact = math.erf(x)
series = erf_approx_series(x)
rational = erf_approx_rational(x)
print(f"Exakt: {exact:.8f}")
print(f"Reihe: {series:.8f}, Fehler: {abs(exact-series):.2e}")
print(f"Rational: {rational:.8f}, Fehler: {abs(exact-rational):.2e}")
💡 Wichtige Eigenschaften der Fehlerfunktion:
- Sigmoidfunktion: S-förmiger Verlauf zwischen -1 und 1
- Ungerade Funktion: erf(-x) = -erf(x)
- Normalverteilung: Zentrale Rolle bei der CDF
- Physikalische Anwendungen: Lösungen von Diffusionsgleichungen
🔬 Anwendungsgebiete der Fehlerfunktion:
- Statistik: Normalverteilung, Hypothesentests, Qualitätskontrolle
- Physik: Wärmeleitung, Diffusion, Quantenmechanik
- Ingenieurswesen: Signalverarbeitung, Regelungstechnik
- Mathematik: Spezielle Funktionen, Integralrechnung
acos - Arkuskosinus
acot - Arkuskotangens
acsc - Arkuskosekans
asec - Arkussekans
asin - Arkussinus
atan - Arkustangens
atan2 - Arkustangens von y/x
cos - Kosinus
cot - Kotangens
csc - Kosekans
sec - Sekans
sin - Sinus
sinc - Kardinalsinus
tan - Tangens
hypot - Hypotenuse
deg2rad - Grad in Radiant
rad2deg - Radiant in Grad
Hyperbolik
acosh - Arkuskosinus hyperbolikus
asinh - Areasinus hyperbolikus
atanh - Arkustangens hyperbolikus
cosh - Kosinus hyperbolikus
sinh - Sinus hyperbolikus
tanh - Tangens hyperbolikus
Logarithmus
log - Logarithmus zur angegebene Basis
ln - Natürlicher Logarithmus zur Basis e
log10 - Logarithmus zur Basis 10
log2 - Logarithmus zur Basis 2
exp - Exponenten zur Basis e
Aktivierung
Softmax
Sigmoid
Derivate Sigmoid
Logit
Derivate Logit
Softsign
Derivate Softsign
Softplus
Logistic
Gamma
Eulersche Gamma Funktion
Lanczos Gamma-Funktion
Stirling Gamma-Funktion
Log Gamma-Funktion
Beta
Beta Funktion
Logarithmische Beta Funktion
Unvollstaendige Beta Funktion
Inverse unvollstaendige Beta Funktion
Fehlerfunktionen
erf - Fehlerfunktion
erfc - komplementäre Fehlerfunktion
Kombinatorik
Fakultät
Semifakultät
Steigende Fakultät
Fallende Fakultät
Subfakultät
Permutationen und Kombinationen
Permutation
Kombinationen
Mittlerer Binomialkoeffizient
Catalan-Zahl
Lah Zahl