Kotangens (cot) Rechner
Berechnung des Kotangens eines Winkels mit mathematischen Eigenschaften
Geben Sie den Winkel ein (in Grad oder Radiant) und klicken Sie auf Berechnen um den entsprechenden Kotangenswert zu ermitteln. Der Kotangens ist der Kehrwert des Tangens.
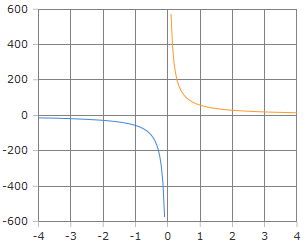
Graphische Darstellung der cot-Funktion
Kotangens (Cotangent)
Kotangens verstehen
Der Kotangens (cot) ist eine der trigonometrischen Funktionen und der Kehrwert des Tangens. Im rechtwinkligen Dreieck ist der Kotangens das Verhältnis von Ankathete zu Gegenkathete. Der Kotangens hat Pole bei Vielfachen von π (180°).
📐 Definition
Im rechtwinkligen Dreieck:
📊 Eigenschaften
- • Definitionsbereich: \(\mathbb{R} \setminus \{k\pi : k \in \mathbb{Z}\}\)
- • Wertebereich: \(\mathbb{R}\)
- • Periode: \(\pi\) rad = \(180°\)
- • Ungerade Funktion: \(\cot(-x) = -\cot(x)\)
🔬 Anwendungen
- • Geometrie und Trigonometrie
- • Optik (Brechungsgesetze)
- • Astronomie (Höhenwinkel)
- • Ingenieurswesen (Steigungen)
⭐ Spezielle Werte
- • \(\cot(30°) = \sqrt{3}\)
- • \(\cot(45°) = 1\)
- • \(\cot(60°) = \frac{1}{\sqrt{3}}\)
- • \(\cot(90°) = 0\)
- • \(\cot(0°) = \infty\) (undefiniert)
Mathematische Eigenschaften
📐 Grundbeziehungen
Wichtige Identitäten des Kotangens:
\[\cot(\alpha) = \frac{1}{\tan(\alpha)} = \frac{\cos(\alpha)}{\sin(\alpha)}\] \[\cot(-x) = -\cot(x) \text{ (ungerade Funktion)}\] \[\cot(x + \pi) = \cot(x) \text{ (Periodizität)}\] \[\cot\left(\frac{\pi}{2} - x\right) = \tan(x)\]
🔄 Additionstheoreme
Zusammenhänge mit Winkelsummen und -differenzen:
\[\cot(a + b) = \frac{\cot(a)\cot(b) - 1}{\cot(a) + \cot(b)}\] \[\cot(a - b) = \frac{\cot(a)\cot(b) + 1}{\cot(b) - \cot(a)}\] \[\cot(2x) = \frac{\cot^2(x) - 1}{2\cot(x)}\] \[\cot\left(\frac{x}{2}\right) = \frac{1 + \cos(x)}{\sin(x)}\]
📊 Ableitung und Integration
Differential- und Integralrechnung:
\[\frac{d}{dx}\cot(x) = -\csc^2(x) = -\frac{1}{\sin^2(x)}\] \[\int \cot(x) \, dx = \ln|\sin(x)| + C\] \[\frac{d^2}{dx^2}\cot(x) = 2\cot(x)\csc^2(x)\] \[\int \cot(ax) \, dx = \frac{1}{a}\ln|\sin(ax)| + C\]
Beachte: Die Ableitung des Kotangens ist immer negativ
Praktische Berechnungsbeispiele
📝 Beispiel 1: Rechtwinkliges Dreieck
Aufgabe: Ankathete aus Gegenkathete und Winkel berechnen
Gegeben: Gegenkathete \(a = 5\), Winkel \(\alpha = 30°\)
Berechnung:
\[\cot(30°) = \frac{b}{a} = \frac{b}{5}\] \[b = 5 \cdot \cot(30°) = 5 \cdot \sqrt{3} \approx 5 \cdot 1{,}732 = 8{,}66\] \[\text{Ankathete: } b \approx 8{,}66 \text{ Einheiten}\]
Verifikation: \(\cot(30°) = \sqrt{3} \approx 1{,}732\) ✓
📝 Beispiel 2: Spezielle Winkel
Aufgabe: Wichtige Kotangenswerte merken
Berechnung:
\[\cot(30°) = \sqrt{3} \approx 1{,}732\] \[\cot(45°) = 1\] \[\cot(60°) = \frac{1}{\sqrt{3}} \approx 0{,}577\] \[\cot(90°) = 0\] \[\cot(120°) = -\frac{1}{\sqrt{3}} \approx -0{,}577\] \[\cot(135°) = -1\]
Merkhilfe: \(\cot(\alpha) = \frac{1}{\tan(\alpha)}\) - Kehrwert des Tangens
📝 Beispiel 3: Steigungsberechnung
Aufgabe: Horizontale Entfernung bei Steigung
Gegeben: Höhenunterschied \(h = 10\) m, Steigungswinkel \(\alpha = 15°\)
Berechnung:
\[\text{Horizontale Entfernung: } d = h \cdot \cot(\alpha)\] \[d = 10 \cdot \cot(15°) = 10 \cdot 3{,}732 = 37{,}32 \text{ m}\] \[\text{Steigung in Prozent: } s = \frac{h}{d} \cdot 100\% = \frac{10}{37{,}32} \cdot 100\% \approx 26{,}8\%\]
Anwendung: Straßenbau, Architektur, Vermessungswesen
Pole und Asymptoten
⚠️ Polstellen
- • Bei \(x = k\pi\) (k ganzzahlig)
- • \(\cot(0°) = \infty\) (undefiniert)
- • \(\cot(180°) = \infty\) (undefiniert)
- • Vertikale Asymptoten
🔢 Grenzverhalten
- • \(\lim_{x \to 0^+} \cot(x) = +\infty\)
- • \(\lim_{x \to 0^-} \cot(x) = -\infty\)
- • Periode: \(180°\) = \(\pi\) rad
- • Stetig außer an Polstellen
Vergleich der trigonometrischen Funktionen
sin(x)
Sinus
Gegenkathete/Hypotenuse
Wertebereich: [-1, 1]
Keine Pole
cos(x)
Kosinus
Ankathete/Hypotenuse
Wertebereich: [-1, 1]
Keine Pole
tan(x)
Tangens
Gegenkathete/Ankathete
Wertebereich: \(\mathbb{R}\)
Pole bei \(\frac{\pi}{2} + k\pi\)
cot(x)
Kotangens
Ankathete/Gegenkathete
Wertebereich: \(\mathbb{R}\)
Pole bei \(k\pi\)
💡 Wichtige Eigenschaften der cot-Funktion:
- Definitionsbereich: \(\mathbb{R} \setminus \{k\pi : k \in \mathbb{Z}\}\)
- Wertebereich: \(\mathbb{R}\) (alle reellen Zahlen)
- Periode: \(\pi\) rad = \(180°\)
- Symmetrie: Ungerade Funktion: \(\cot(-x) = -\cot(x)\)
🔬 Anwendungsgebiete der cot-Funktion:
- Geometrie: Dreieckberechnung und Winkelverhältnisse
- Vermessungswesen: Höhen- und Entfernungsmessung
- Optik: Brechungsgesetze und Strahlengänge
- Bauingenieurswesen: Steigungsberechnungen und Neigungen
Taylor-Reihenentwicklung
🔢 Laurent-Reihe von cot(x)
Reihenentwicklung um \(x = 0\) (Laurent-Reihe wegen Pol):
\[\cot(x) = \frac{1}{x} - \frac{x}{3} - \frac{x^3}{45} - \frac{2x^5}{945} - \ldots\] \[\cot(x) = \frac{1}{x} - \sum_{n=1}^{\infty} \frac{2^{2n} B_{2n}}{(2n)!} x^{2n-1}\] \[\text{Gültig für } 0 < |x| < \pi\]
Besonderheit: \(B_{2n}\) sind Bernoulli-Zahlen, \(\frac{1}{x}\)-Term wegen Pol bei x=0
Praktische Integralformeln mit cot
| Integral | Stammfunktion | Besonderheiten |
|---|---|---|
| \(\int \cot(x) dx\) | \(\ln|\sin(x)| + C\) | Grundintegral |
| \(\int \cot(ax) dx\) | \(\frac{1}{a}\ln|\sin(ax)| + C\) | Lineare Substitution |
| \(\int \cot^2(x) dx\) | \(-\cot(x) - x + C\) | Trigonometrische Identität |
| \(\int x \cot(x) dx\) | Keine elementare Form | Reihenentwicklung nötig |
acos - Arkuskosinus
acot - Arkuskotangens
acsc - Arkuskosekans
asec - Arkussekans
asin - Arkussinus
atan - Arkustangens
atan2 - Arkustangens von y/x
cos - Kosinus
cot - Kotangens
csc - Kosekans
sec - Sekans
sin - Sinus
sinc - Kardinalsinus
tan - Tangens
hypot - Hypotenuse
deg2rad - Grad in Radiant
rad2deg - Radiant in Grad
Hyperbolik
acosh - Arkuskosinus hyperbolikus
asinh - Areasinus hyperbolikus
atanh - Arkustangens hyperbolikus
cosh - Kosinus hyperbolikus
sinh - Sinus hyperbolikus
tanh - Tangens hyperbolikus
Logarithmus
log - Logarithmus zur angegebene Basis
ln - Natürlicher Logarithmus zur Basis e
log10 - Logarithmus zur Basis 10
log2 - Logarithmus zur Basis 2
exp - Exponenten zur Basis e
Aktivierung
Softmax
Sigmoid
Derivate Sigmoid
Logit
Derivate Logit
Softsign
Derivate Softsign
Softplus
Logistic
Gamma
Eulersche Gamma Funktion
Lanczos Gamma-Funktion
Stirling Gamma-Funktion
Log Gamma-Funktion
Beta
Beta Funktion
Logarithmische Beta Funktion
Unvollstaendige Beta Funktion
Inverse unvollstaendige Beta Funktion
Fehlerfunktionen
erf - Fehlerfunktion
erfc - komplementäre Fehlerfunktion
Kombinatorik
Fakultät
Semifakultät
Steigende Fakultät
Fallende Fakultät
Subfakultät
Permutationen und Kombinationen
Permutation
Kombinationen
Mittlerer Binomialkoeffizient
Catalan-Zahl
Lah Zahl