Hyperbolischer Tangens (tanh) Rechner
Berechnung des hyperbolischen Tangens eines Winkels mit mathematischen Eigenschaften
Geben Sie den Winkel ein und klicken Sie auf Berechnen um den hyperbolischen Tangens zu ermitteln. Der hyperbolische Tangens ist für alle reellen Zahlen definiert und hat einen Wertebereich von (-1, 1).
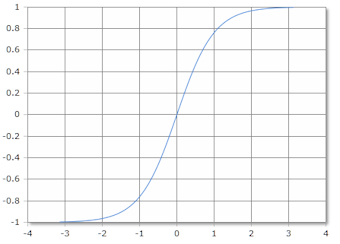
Graphische Darstellung der tanh-Funktion
Hyperbolischer Tangens
Hyperbolischer Tangens verstehen
Der hyperbolische Tangens (tanh) ist eine fundamentale hyperbolische Funktion. Er ist für alle reellen Zahlen definiert und hat wichtige Eigenschaften: Er ist eine ungerade Funktion (tanh(-x) = -tanh(x)) und sein Wertebereich ist (-1, 1). In der künstlichen Intelligenz wird tanh häufig als Aktivierungsfunktion verwendet.
📐 Definition
Exponentialform:
📊 Eigenschaften
- • Definitionsbereich: \((-\infty, \infty)\)
- • Wertebereich: \((-1, 1)\)
- • Ungerade Funktion: \(\tanh(-x) = -\tanh(x)\)
- • Nullstelle: \(\tanh(0) = 0\)
🔬 Anwendungen
- • Künstliche Intelligenz (Aktivierungsfunktion)
- • Signalverarbeitung
- • Relativitätstheorie
- • Differentialgleichungen
⭐ Spezielle Werte
- • \(\tanh(0) = 0\)
- • \(\tanh(1) \approx 0{,}762\)
- • \(\tanh(-1) \approx -0{,}762\)
- • \(\lim_{x \to \infty} \tanh(x) = 1\)
Mathematische Eigenschaften
📐 Grundformel
Definition des hyperbolischen Tangens:
\[\tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}}\] \[\text{für alle } x \in \mathbb{R}\]
Alternative Darstellung: \(\tanh(x) = \frac{e^{2x} - 1}{e^{2x} + 1}\)
🔄 Wichtige Beziehungen
Zusammenhänge mit anderen Funktionen:
\[\tanh^2(x) = 1 - \text{sech}^2(x) = 1 - \frac{1}{\cosh^2(x)}\] \[\tanh(x + y) = \frac{\tanh(x) + \tanh(y)}{1 + \tanh(x)\tanh(y)}\] \[\tanh(2x) = \frac{2\tanh(x)}{1 + \tanh^2(x)}\] \[\tanh(-x) = -\tanh(x) \text{ (ungerade Funktion)}\]
📊 Ableitung und Integration
Differential- und Integralrechnung:
\[\frac{d}{dx}\tanh(x) = \text{sech}^2(x) = 1 - \tanh^2(x)\] \[\int \tanh(x) \, dx = \ln(\cosh(x)) + C\] \[\int \text{sech}^2(x) \, dx = \tanh(x) + C\]
Beachte: Die Ableitung ist immer positiv, tanh ist streng monoton steigend
Praktische Berechnungsbeispiele
📝 Beispiel 1: Grundwerte berechnen
Aufgabe: Berechnung verschiedener tanh-Werte
Berechnung:
\[\tanh(0) = \frac{e^0 - e^{-0}}{e^0 + e^{-0}} = \frac{1 - 1}{1 + 1} = 0\] \[\tanh(1) = \frac{e^1 - e^{-1}}{e^1 + e^{-1}} = \frac{e - \frac{1}{e}}{e + \frac{1}{e}} \approx 0{,}762\] \[\tanh(\ln(2)) = \frac{2 - \frac{1}{2}}{2 + \frac{1}{2}} = \frac{1{,}5}{2{,}5} = 0{,}6\]
Symmetrie: \(\tanh(-1) = -\tanh(1) = -0{,}762\) ✓
📝 Beispiel 2: Neuronale Netze (Aktivierungsfunktion)
Aufgabe: Anwendung als Aktivierungsfunktion
Eingabe: Gewichtete Summe \(z = 2{,}5\)
Berechnung:
\[\text{Aktivierung: } a = \tanh(z) = \tanh(2{,}5)\] \[a = \frac{e^{2{,}5} - e^{-2{,}5}}{e^{2{,}5} + e^{-2{,}5}} \approx 0{,}987\] \[\text{Ableitung: } \frac{da}{dz} = 1 - \tanh^2(2{,}5) = 1 - 0{,}987^2 \approx 0{,}026\]
Vorteil: Ausgabe zwischen -1 und 1, differenzierbar, verhindert Gradient Explosion
📝 Beispiel 3: Geschwindigkeitsaddition (Relativität)
Aufgabe: Rapidität in der speziellen Relativitätstheorie
Gegeben: Rapidität \(\phi = 1{,}5\)
Berechnung:
\[\text{Geschwindigkeit: } \frac{v}{c} = \tanh(\phi) = \tanh(1{,}5)\] \[\frac{v}{c} = \frac{e^{1{,}5} - e^{-1{,}5}}{e^{1{,}5} + e^{-1{,}5}} \approx 0{,}905\] \[\text{Also: } v \approx 0{,}905c = 271{.}000{.}000 \text{ m/s}\]
Physik: tanh garantiert, dass \(v < c\) (Lichtgeschwindigkeit)
Numerische und geometrische Eigenschaften
📊 Asymptotisches Verhalten
- • Für \(x \to +\infty\): \(\tanh(x) \to 1\)
- • Für \(x \to -\infty\): \(\tanh(x) \to -1\)
- • Monoton steigend für alle \(x\)
- • Horizontale Asymptoten bei \(y = \pm 1\)
🔢 Reihenentwicklung
- • Taylor-Reihe um \(x = 0\):
- • \(\tanh(x) = x - \frac{x^3}{3} + \frac{2x^5}{15} - \frac{17x^7}{315} + \ldots\)
- • \(\tanh(x) = \sum_{n=1}^{\infty} \frac{B_{2n}(2^{2n}-1)2^{2n}}{(2n)!}x^{2n-1}\)
- • Konvergenzradius: \(R = \frac{\pi}{2}\)
Vergleich der hyperbolischen Funktionen
sinh(x)
Hyperbolischer Sinus
\(\sinh(x) = \frac{e^x - e^{-x}}{2}\)
Ungerade Funktion
Def: \(\mathbb{R} \to \mathbb{R}\)
cosh(x)
Hyperbolischer Kosinus
\(\cosh(x) = \frac{e^x + e^{-x}}{2}\)
Gerade Funktion
Def: \(\mathbb{R} \to [1,\infty)\)
tanh(x)
Hyperbolischer Tangens
\(\tanh(x) = \frac{\sinh(x)}{\cosh(x)}\)
Beschränkt auf (-1,1)
Def: \(\mathbb{R} \to (-1,1)\)
Geometrische Interpretation
🔵 Einheitshyperbel und tanh
Zusammenhang mit hyperbolischen Koordinaten:
\[x^2 - y^2 = 1 \text{ (Einheitshyperbel)}\] \[\text{Parametrisierung: } x = \cosh(t), \quad y = \sinh(t)\] \[\text{Steigung: } \frac{dy}{dx} = \frac{\sinh(t)}{\cosh(t)} = \tanh(t)\] \[\text{Geschwindigkeit: } \left|\frac{d}{dt}(x, y)\right|^2 = \sinh^2(t) + \cosh^2(t) = \cosh(2t)\]
Interpretation: tanh beschreibt die "normalisierte Geschwindigkeit" auf der Hyperbel
💡 Wichtige Eigenschaften der tanh-Funktion:
- Beschränkt: \(-1 < \tanh(x) < 1\) für alle \(x \in \mathbb{R}\)
- Ungerade Funktion: \(\tanh(-x) = -\tanh(x)\)
- Monoton steigend: \(\tanh'(x) = 1 - \tanh^2(x) > 0\)
- Aktivierungsfunktion: Beliebte Wahl in neuronalen Netzen
🔬 Anwendungsgebiete der tanh-Funktion:
- Künstliche Intelligenz: Aktivierungsfunktion in neuronalen Netzen
- Signalverarbeitung: Weiche Begrenzung und Normalisierung
- Relativitätstheorie: Geschwindigkeitskomposition und Rapidität
- Kontrolltheorie: Sättigungsfunktionen und Stabilitätsanalyse
Vollständige Taylor-Reihenentwicklung
🔢 Taylor-Reihe von tanh(x)
Vollständige Reihenentwicklung um \(x = 0\):
\[\tanh(x) = \sum_{n=1}^{\infty} \frac{B_{2n}(2^{2n}-1)2^{2n}}{(2n)!}x^{2n-1\] \[= x - \frac{x^3}{3} + \frac{2x^5}{15} - \frac{17x^7}{315} + \frac{62x^9}{2835} - \ldots\] \[\text{Konvergenzradius: } R = \frac{\pi}{2}\]
Beachte: \(B_{2n}\) sind die Bernoulli-Zahlen
Praktische Integralformeln mit tanh
| Integral | Stammfunktion | Anwendung |
|---|---|---|
| \(\int \tanh(x) dx\) | \(\ln(\cosh(x)) + C\) | Grundintegral |
| \(\int \text{sech}^2(x) dx\) | \(\tanh(x) + C\) | Ableitung von tanh |
| \(\int x \tanh(x) dx\) | \(x \ln(\cosh(x)) - \text{Li}_2(-e^{2x}) + C\) | Partielle Integration |
| \(\int \tanh^2(x) dx\) | \(x - \tanh(x) + C\) | Quadratische Form |
Anwendungen in der künstlichen Intelligenz
🤖 Aktivierungsfunktion in neuronalen Netzen
Eigenschaften und Verwendung:
\[\text{Output: } y = \tanh(w \cdot x + b)\] \[\text{Gradient: } \frac{\partial y}{\partial x} = w(1 - \tanh^2(w \cdot x + b))\] \[\text{Vorteil: } -1 \leq y \leq 1 \text{ (zentriert um Null)}\] \[\text{Problem: } \text{Vanishing Gradient für große } |x|\]
Vergleich zu anderen Aktivierungsfunktionen:
- Sigmoid: Ausgabe (0,1), aber nicht nullzentriert
- ReLU: Ausgabe [0,∞), löst Vanishing Gradient Problem
- Tanh: Ausgabe (-1,1), nullzentriert, aber Vanishing Gradient
🎯 LSTM und GRU Gating-Mechanismen
Anwendung in rekurrenten neuronalen Netzen:
\[\text{Output Gate: } o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o)\] \[\text{Cell State: } \tilde{C}_t = \tanh(W_C \cdot [h_{t-1}, x_t] + b_C)\] \[\text{Hidden State: } h_t = o_t \odot \tanh(C_t)\] \[\text{Wobei: } \sigma = \text{Sigmoid}, \odot = \text{Element-wise Produkt}\]
Rolle von tanh: Reguliert die Information zwischen -1 und 1
acos - Arkuskosinus
acot - Arkuskotangens
acsc - Arkuskosekans
asec - Arkussekans
asin - Arkussinus
atan - Arkustangens
atan2 - Arkustangens von y/x
cos - Kosinus
cot - Kotangens
csc - Kosekans
sec - Sekans
sin - Sinus
sinc - Kardinalsinus
tan - Tangens
hypot - Hypotenuse
deg2rad - Grad in Radiant
rad2deg - Radiant in Grad
Hyperbolik
acosh - Arkuskosinus hyperbolikus
asinh - Areasinus hyperbolikus
atanh - Arkustangens hyperbolikus
cosh - Kosinus hyperbolikus
sinh - Sinus hyperbolikus
tanh - Tangens hyperbolikus
Logarithmus
log - Logarithmus zur angegebene Basis
ln - Natürlicher Logarithmus zur Basis e
log10 - Logarithmus zur Basis 10
log2 - Logarithmus zur Basis 2
exp - Exponenten zur Basis e
Aktivierung
Softmax
Sigmoid
Derivate Sigmoid
Logit
Derivate Logit
Softsign
Derivate Softsign
Softplus
Logistic
Gamma
Eulersche Gamma Funktion
Lanczos Gamma-Funktion
Stirling Gamma-Funktion
Log Gamma-Funktion
Beta
Beta Funktion
Logarithmische Beta Funktion
Unvollstaendige Beta Funktion
Inverse unvollstaendige Beta Funktion
Fehlerfunktionen
erf - Fehlerfunktion
erfc - komplementäre Fehlerfunktion
Kombinatorik
Fakultät
Semifakultät
Steigende Fakultät
Fallende Fakultät
Subfakultät
Permutationen und Kombinationen
Permutation
Kombinationen
Mittlerer Binomialkoeffizient
Catalan-Zahl
Lah Zahl