Hypotenuse (hypot) Rechner
Berechnung der Hypotenuse mit dem Satz des Pythagoras
Geben Sie die beiden Katheten eines rechtwinkligen Dreiecks ein und klicken Sie auf Berechnen um die Hypotenuse zu ermitteln. Die hypot-Funktion verwendet den Satz des Pythagoras für eine numerisch stabile Berechnung.
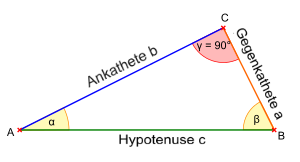
Rechtwinkliges Dreieck
Katheten a, b und Hypotenuse c
Hypotenuse und Pythagoras verstehen
Die hypot-Funktion berechnet die Hypotenuse eines rechtwinkligen Dreiecks aus den beiden Katheten. Sie basiert auf dem berühmten Satz des Pythagoras und ist eine der wichtigsten mathematischen Funktionen für geometrische Berechnungen. Die Funktion ist numerisch optimiert und vermeidet Über- oder Unterläufe bei sehr großen oder kleinen Werten.
📐 Satz des Pythagoras
Fundamentales Theorem:
📊 Eigenschaften
- • Hypotenuse ist längste Seite
- • Gegenüber dem rechten Winkel
- • \(c > a\) und \(c > b\)
- • Numerisch stabile Berechnung
🔬 Anwendungen
- • Geometrie und Trigonometrie
- • Entfernungsberechnung (2D/3D)
- • Computergrafik und CAD
- • Physik (Vektorlängen)
⭐ Pythagoräische Tripel
- • (3, 4, 5) → c = 5
- • (5, 12, 13) → c = 13
- • (8, 15, 17) → c = 17
- • (1, 1, √2) → c ≈ 1.414
Mathematische Grundlagen
📐 Der Satz des Pythagoras
Fundamentaler Satz der Geometrie:
\[a^2 + b^2 = c^2\] \[\text{Daraus folgt: } c = \sqrt{a^2 + b^2}\] \[\text{hypot}(a, b) = \sqrt{a^2 + b^2}\]
Bedingung: Gilt nur für rechtwinklige Dreiecke (ein Winkel = 90°)
🔄 Numerische Stabilität
Warum hypot() besser als √(a² + b²) ist:
\[\text{Problem: } a^2 + b^2 \text{ kann bei großen Werten überlaufen}\] \[\text{Lösung: } \text{hypot}(a, b) = |a| \sqrt{1 + \left(\frac{b}{a}\right)^2} \text{ für } |a| \geq |b|\] \[\text{Algorithmus vermeidet Unter-/Überläufe}\]
Vorteil: Präzise Berechnung auch bei extremen Werten
📊 Erweiterte Formen
Verallgemeinerungen der hypot-Funktion:
\[\text{2D: } \text{hypot}(x, y) = \sqrt{x^2 + y^2}\] \[\text{3D: } \text{hypot}(x, y, z) = \sqrt{x^2 + y^2 + z^2}\] \[\text{nD: } \text{hypot}(x_1, x_2, \ldots, x_n) = \sqrt{\sum_{i=1}^{n} x_i^2}\]
Anwendung: Berechnung der euklidischen Norm (Länge) von Vektoren
Praktische Berechnungsbeispiele
📝 Beispiel 1: Klassisches 3-4-5 Dreieck
Aufgabe: Hypotenuse eines Dreiecks mit Katheten 3 und 4
Berechnung:
\[c = \text{hypot}(3, 4) = \sqrt{3^2 + 4^2}\] \[c = \sqrt{9 + 16} = \sqrt{25} = 5\] \[\text{Verifikation: } 3^2 + 4^2 = 9 + 16 = 25 = 5^2 \checkmark\]
Ergebnis: Die Hypotenuse ist exakt 5 Einheiten lang
📝 Beispiel 2: Entfernungsberechnung
Aufgabe: Entfernung zwischen zwei Punkten
Gegeben: Punkt A(2, 3) und Punkt B(8, 11)
Berechnung:
\[\Delta x = 8 - 2 = 6\] \[\Delta y = 11 - 3 = 8\] \[d = \text{hypot}(6, 8) = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10\]
Anwendung: GPS-Navigation, Computergrafik, Robotik
📝 Beispiel 3: Dachkonstruktion
Aufgabe: Sparrenlänge für ein Dach berechnen
Gegeben: Dachbreite = 12 m, Dachhöhe = 5 m
Berechnung:
\[\text{Halbe Dachbreite: } a = \frac{12}{2} = 6 \text{ m}\] \[\text{Dachhöhe: } b = 5 \text{ m}\] \[\text{Sparrenlänge: } c = \text{hypot}(6, 5) = \sqrt{6^2 + 5^2}\] \[c = \sqrt{36 + 25} = \sqrt{61} \approx 7{,}81 \text{ m}\]
Praxis: Materialberechnung, Statik, Kosten
Pythagoräische Tripel
🔢 Bekannte ganzzahlige Lösungen
Tripel natürlicher Zahlen (a, b, c) mit a² + b² = c²:
| Kathete a | Kathete b | Hypotenuse c | Verhältnis a:b:c | Besonderheit |
|---|---|---|---|---|
| 3 | 4 | 5 | 3:4:5 | Kleinstes primitives Tripel |
| 5 | 12 | 13 | 5:12:13 | Häufig in Aufgaben |
| 8 | 15 | 17 | 8:15:17 | Nächstes primitives Tripel |
| 7 | 24 | 25 | 7:24:25 | Großer Unterschied in Katheten |
| 1 | 1 | √2 | 1:1:√2 | 45°-45°-90° Dreieck |
Anwendungen in verschiedenen Bereichen
🏗️ Bauingenieurswesen
- • Dachsparren und Träger
- • Diagonalverstrebungen
- • Treppen und Rampen
- • Fundamentabmessungen
💻 Informatik
- • Computergrafik (Pixelabstände)
- • Spieleentwicklung (Kollision)
- • Bildverarbeitung
- • Machine Learning (Distanzen)
🧭 Navigation
- • GPS-Koordinaten
- • Entfernungsmessung
- • Seekarten und Luftfahrt
- • Triangulation
🔬 Physik
- • Vektoraddition
- • Kräftezerlegung
- • Schwingungen und Wellen
- • Kinematik (Geschwindigkeit)
Erweiterte Konzepte
🌐 3D-Erweiterung
Hypotenuse in drei Dimensionen:
\[\text{3D-Abstand: } d = \sqrt{x^2 + y^2 + z^2}\] \[\text{Beispiel: } A(1, 2, 3) \text{ zu } B(4, 6, 8)\] \[\Delta x = 3, \Delta y = 4, \Delta z = 5\] \[d = \sqrt{3^2 + 4^2 + 5^2} = \sqrt{9 + 16 + 25} = \sqrt{50} \approx 7{,}07\]
Anwendung: 3D-Grafik, Robotik, Astronomie
📊 Euklidische Norm
Mathematische Verallgemeinerung:
\[\text{Vektor: } \vec{v} = (v_1, v_2, \ldots, v_n)\] \[\text{Euklidische Norm: } \|\vec{v}\| = \sqrt{v_1^2 + v_2^2 + \cdots + v_n^2}\] \[\text{Eigenschaften:}\] \[\|\vec{v}\| \geq 0 \text{ (nicht-negativ)}\] \[\|\alpha \vec{v}\| = |\alpha| \|\vec{v}\| \text{ (homogen)}\] \[\|\vec{u} + \vec{v}\| \leq \|\vec{u}\| + \|\vec{v}\| \text{ (Dreiecksungleichung)}\]
💡 Wichtige Eigenschaften der hypot-Funktion:
- Numerisch stabil: Vermeidet Über-/Unterläufe bei extremen Werten
- Symmetrisch: hypot(a, b) = hypot(b, a)
- Homogen: hypot(ka, kb) = k · hypot(a, b) für k > 0
- Erweiterbar: Kann auf beliebige Dimensionen verallgemeinert werden
🔬 Anwendungsgebiete der hypot-Funktion:
- Geometrie: Entfernungsberechnung, Dreieckslehre
- Physik: Vektoroperationen, Kraftzerlegung
- Informatik: Computergrafik, Bildverarbeitung, Algorithmen
- Ingenieurswesen: Konstruktion, Vermessung, CAD-Systeme
Historischer Hintergrund
📜 Geschichte des Pythagoras
Entwicklung und Bedeutung:
Antike (ca. 500 v. Chr.): Pythagoras von Samos
Babylonier (ca. 1900-1600 v. Chr.): Bereits bekannte Tripel
Moderne Zeit: Numerisch stabile Implementierungen
Heute: Standard in allen Programmiersprachen
Bedeutung: Einer der fundamentalsten mathematischen Sätze
Programmierung und Implementation
💻 Algorithmus
Numerisch stabile Implementierung:
function hypot(a, b) {
a = Math.abs(a);
b = Math.abs(b);
if (a > b) [a, b] = [b, a]; // a ≤ b
if (a === 0) return b;
var ratio = a / b;
return b * Math.sqrt(1 + ratio * ratio);
}
Vorteil: Vermeidet Overflow bei großen und Underflow bei kleinen Werten
acos - Arkuskosinus
acot - Arkuskotangens
acsc - Arkuskosekans
asec - Arkussekans
asin - Arkussinus
atan - Arkustangens
atan2 - Arkustangens von y/x
cos - Kosinus
cot - Kotangens
csc - Kosekans
sec - Sekans
sin - Sinus
sinc - Kardinalsinus
tan - Tangens
hypot - Hypotenuse
deg2rad - Grad in Radiant
rad2deg - Radiant in Grad
Hyperbolik
acosh - Arkuskosinus hyperbolikus
asinh - Areasinus hyperbolikus
atanh - Arkustangens hyperbolikus
cosh - Kosinus hyperbolikus
sinh - Sinus hyperbolikus
tanh - Tangens hyperbolikus
Logarithmus
log - Logarithmus zur angegebene Basis
ln - Natürlicher Logarithmus zur Basis e
log10 - Logarithmus zur Basis 10
log2 - Logarithmus zur Basis 2
exp - Exponenten zur Basis e
Aktivierung
Softmax
Sigmoid
Derivate Sigmoid
Logit
Derivate Logit
Softsign
Derivate Softsign
Softplus
Logistic
Gamma
Eulersche Gamma Funktion
Lanczos Gamma-Funktion
Stirling Gamma-Funktion
Log Gamma-Funktion
Beta
Beta Funktion
Logarithmische Beta Funktion
Unvollstaendige Beta Funktion
Inverse unvollstaendige Beta Funktion
Fehlerfunktionen
erf - Fehlerfunktion
erfc - komplementäre Fehlerfunktion
Kombinatorik
Fakultät
Semifakultät
Steigende Fakultät
Fallende Fakultät
Subfakultät
Permutationen und Kombinationen
Permutation
Kombinationen
Mittlerer Binomialkoeffizient
Catalan-Zahl
Lah Zahl