Softsign Funktion Rechner
Online Rechner für die Softsign-Aktivierungsfunktion
Geben Sie das Argument (x) ein und klicken Sie auf Berechnen um die Softsign-Funktion zu ermitteln. Die Softsign-Funktion ist eine alternative Aktivierungsfunktion zu Tanh mit ähnlicher S-Form, aber langsamerer Sättigung und weniger steilen Gradienten.
💡 Softsign-Funktion
\(\text{softsign}(x) = \frac{x}{1 + |x|}\)
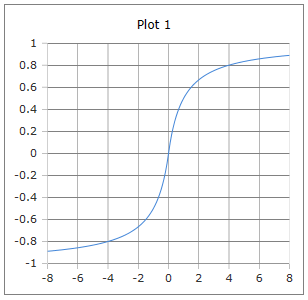
Die charakteristische S-förmige Kurve der Softsign-Funktion
Die Softsign-Funktion verstehen
Die Softsign-Funktion ist eine S-förmige Aktivierungsfunktion für neuronale Netze, die als Alternative zur Tanh-Funktion entwickelt wurde. Sie zeichnet sich durch ihre einfache Berechnung und langsamere Sättigung aus, was zu weniger extremen Gradienten führt. Mit der Formel softsign(x) = x/(1+|x|) bietet sie einen Wertebereich von (-1, 1) und eine zentrale Symmetrie um den Ursprung.
📊 Grunddefinition
Mathematische Form:
📈 Eigenschaften
- • Wertebereich: (-1, 1)
- • softsign(0) = 0
- • Punktsymmetrie zum Ursprung
- • Langsamere Sättigung als Tanh
🔬 Anwendungen
- • Aktivierungsfunktion in NN
- • Alternative zu Tanh
- • Normalisierung von Daten
- • Glättung von Entscheidungen
⭐ Vorteile
- • Einfache Berechnung
- • Keine Exponentialfunktion
- • Sanfte Gradienten
- • Numerisch stabil
Mathematische Grundlagen
📊 Verschiedene Darstellungen
Alternative Formulierungen der Softsign-Funktion:
\[\text{softsign}(x) = \frac{x}{1 + |x|} \quad \text{(Standard-Form)}\] \[\text{softsign}(x) = \begin{cases} \frac{x}{1 + x} & \text{wenn } x \geq 0 \\ \frac{x}{1 - x} & \text{wenn } x < 0 \end{cases}\] \[\text{softsign}(x) = \text{sign}(x) \cdot \frac{|x|}{1 + |x|} \quad \text{(Aufgeteilte Form)}\]
🔄 Vergleich mit Tanh
Softsign vs. Tanh-Funktion:
\[\text{Tanh: } \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} = \frac{e^{2x} - 1}{e^{2x} + 1}\] \[\text{Softsign: } \text{softsign}(x) = \frac{x}{1 + |x|}\] \[\text{Gemeinsam: } f(0) = 0, \text{ Wertebereich } (-1, 1), \text{ Punktsymmetrie}\] \[\text{Unterschied: Tanh sättigt schneller, Softsign langsamer}\]
📈 Ableitungen und Eigenschaften
Wichtige mathematische Eigenschaften:
\[\text{Ableitung: } \frac{d}{dx}\text{softsign}(x) = \frac{1}{(1 + |x|)^2}\] \[\text{Für } x > 0: \frac{d}{dx}\text{softsign}(x) = \frac{1}{(1 + x)^2}\] \[\text{Für } x < 0: \frac{d}{dx}\text{softsign}(x) = \frac{1}{(1 - x)^2}\] \[\text{Maximum der Ableitung bei } x = 0: \text{softsign}'(0) = 1\]
Praktische Berechnungsbeispiele
📝 Beispiel 1: Grundlegende Berechnungen
Aufgabe: Softsign-Werte für verschiedene Eingaben
Berechnung:
\[\text{softsign}(-2) = \frac{-2}{1 + |-2|} = \frac{-2}{1 + 2} = \frac{-2}{3} \approx -0{,}667\] \[\text{softsign}(-1) = \frac{-1}{1 + 1} = \frac{-1}{2} = -0{,}5\] \[\text{softsign}(0) = \frac{0}{1 + 0} = 0\] \[\text{softsign}(1) = \frac{1}{1 + 1} = \frac{1}{2} = 0{,}5\] \[\text{softsign}(2) = \frac{2}{1 + 2} = \frac{2}{3} \approx 0{,}667\]
Symmetrie: softsign(-x) = -softsign(x) für alle x
📝 Beispiel 2: Vergleich mit Tanh
Aufgabe: Unterschiede zwischen Softsign und Tanh
Eingabe: x = 2
Berechnung:
\[\text{Softsign: } \text{softsign}(2) = \frac{2}{1 + 2} = \frac{2}{3} \approx 0{,}667\] \[\text{Tanh: } \tanh(2) = \frac{e^4 - 1}{e^4 + 1} \approx \frac{54{,}6 - 1}{54{,}6 + 1} \approx 0{,}964\] \[\text{Verhältnis: } \frac{\text{softsign}(2)}{\tanh(2)} \approx \frac{0{,}667}{0{,}964} \approx 0{,}692\] \[\text{Beobachtung: Softsign sättigt langsamer}\]
Verhalten: Bei großen |x| nähert sich Softsign langsamer den Grenzen ±1
📝 Beispiel 3: Neuronales Netzwerk
Aufgabe: Aktivierung in versteckter Schicht
Gegeben: Gewichtete Summe z = 1.5
Berechnung:
\[\text{Aktivierung: } a = \text{softsign}(1{,}5) = \frac{1{,}5}{1 + 1{,}5} = \frac{1{,}5}{2{,}5} = 0{,}6\] \[\text{Ableitung: } \frac{da}{dz} = \frac{1}{(1 + |1{,}5|)^2} = \frac{1}{(2{,}5)^2} = \frac{1}{6{,}25} = 0{,}16\] \[\text{Vergleich Tanh: } \tanh(1{,}5) \approx 0{,}905, \quad \tanh'(1{,}5) \approx 0{,}181\] \[\text{Gradient-Verhalten: Ähnliche Ableitungen, aber andere Aktivierung}\]
Backpropagation: Sanftere Gradienten können stabileres Training fördern
Vor- und Nachteile
✅ Vorteile der Softsign-Funktion
Positive Eigenschaften im Vergleich zu anderen Aktivierungsfunktionen:
\[\text{✓ Einfache Berechnung ohne Exponentialfunktionen}\] \[\text{✓ Numerisch stabil für alle Eingabewerte}\] \[\text{✓ Langsamere Sättigung als Tanh}\] \[\text{✓ Sanfte Gradienten reduzieren Exploding Gradients}\] \[\text{✓ Symmetrisch um den Ursprung}\] \[\text{✓ Kontinuierlich differenzierbar}\]
⚠️ Nachteile und Limitationen
Herausforderungen bei der Verwendung:
\[\text{⚠ Kann zu langsames Lernen verursachen}\] \[\text{⚠ Weniger expressive Power als Tanh für komplexe Muster}\] \[\text{⚠ Begrenzte empirische Evidenz für Überlegenheit}\] \[\text{⚠ Vanishing Gradient Problem bei sehr tiefen Netzen}\] \[\text{⚠ Nicht so weit verbreitet wie ReLU oder Tanh}\]
Vergleichstabelle der Aktivierungsfunktionen
📊 Funktionswerte-Vergleich
| Input x | Softsign | Tanh | Sigmoid | ReLU |
|---|---|---|---|---|
| -3 | -0.750 | -0.995 | 0.047 | 0 |
| -1 | -0.500 | -0.762 | 0.269 | 0 |
| 0 | 0.000 | 0.000 | 0.500 | 0 |
| 1 | 0.500 | 0.762 | 0.731 | 1 |
| 3 | 0.750 | 0.995 | 0.953 | 3 |
| 5 | 0.833 | 0.999 | 0.993 | 5 |
Anwendungen in verschiedenen Bereichen
🧠 Neuronale Netze
- • Alternative zu Tanh in Hidden Layers
- • Sanftere Aktivierung
- • Stabilere Gradienten
- • Experimentelle Architektur
📊 Datenverarbeitung
- • Normalisierung von Signalen
- • Glättung von Entscheidungen
- • Robuste Transformation
- • Outlier-resistente Skalierung
🔬 Forschung
- • Alternative Aktivierungsfunktionen
- • Gradient-Flow-Studien
- • Vergleichende Analysen
- • Theoretische Untersuchungen
⚙️ Spezialanwendungen
- • Numerisch sensible Berechnungen
- • Embedded Systems
- • Low-Power Implementierungen
- • Hardware-freundliche Designs
Implementierung und Code
💻 Code-Implementierungen
Implementierung der Softsign-Funktion:
Python (NumPy):
def softsign(x):
return x / (1 + np.abs(x))
def softsign_derivative(x):
return 1 / ((1 + np.abs(x)) ** 2)
# Vektorisierte Version
def softsign_vectorized(x):
return np.divide(x, 1 + np.abs(x))
TensorFlow/Keras:
tf.nn.softsign(x)
# oder als Layer:
tf.keras.activations.softsign
PyTorch:
torch.nn.functional.softsign(x)
# oder als Layer:
torch.nn.Softsign()
🎯 Praktische Anwendung
Verwendung in neuronalen Netzen:
Keras/TensorFlow Beispiel:
model = tf.keras.Sequential([
tf.keras.layers.Dense(64, activation='softsign'),
tf.keras.layers.Dense(32, activation='softsign'),
tf.keras.layers.Dense(10, activation='softmax')
])
# Oder als benutzerdefinierte Schicht:
class SoftsignLayer(tf.keras.layers.Layer):
def call(self, inputs):
return tf.nn.softsign(inputs)
PyTorch Beispiel:
class Net(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 128)
self.fc2 = nn.Linear(128, 64)
self.fc3 = nn.Linear(64, 10)
self.softsign = nn.Softsign()
def forward(self, x):
x = self.softsign(self.fc1(x))
x = self.softsign(self.fc2(x))
return self.fc3(x)
💡 Wichtige Eigenschaften der Softsign-Funktion:
- Einfachheit: softsign(x) = x/(1+|x|) - keine Exponentialfunktionen
- Wertebereich: (-1, 1) - ähnlich wie Tanh, aber sanftere Sättigung
- Symmetrie: Punktsymmetrie um den Ursprung
- Stabilität: Numerisch stabil für alle Eingabewerte
🔬 Anwendungsgebiete der Softsign-Funktion:
- Neuronale Netze: Alternative Aktivierungsfunktion zu Tanh
- Datenverarbeitung: Sanfte Normalisierung und Glättung
- Embedded Systems: Hardware-freundliche Implementation
- Forschung: Studien zu alternativen Aktivierungsfunktionen
acos - Arkuskosinus
acot - Arkuskotangens
acsc - Arkuskosekans
asec - Arkussekans
asin - Arkussinus
atan - Arkustangens
atan2 - Arkustangens von y/x
cos - Kosinus
cot - Kotangens
csc - Kosekans
sec - Sekans
sin - Sinus
sinc - Kardinalsinus
tan - Tangens
hypot - Hypotenuse
deg2rad - Grad in Radiant
rad2deg - Radiant in Grad
Hyperbolik
acosh - Arkuskosinus hyperbolikus
asinh - Areasinus hyperbolikus
atanh - Arkustangens hyperbolikus
cosh - Kosinus hyperbolikus
sinh - Sinus hyperbolikus
tanh - Tangens hyperbolikus
Logarithmus
log - Logarithmus zur angegebene Basis
ln - Natürlicher Logarithmus zur Basis e
log10 - Logarithmus zur Basis 10
log2 - Logarithmus zur Basis 2
exp - Exponenten zur Basis e
Aktivierung
Softmax
Sigmoid
Derivate Sigmoid
Logit
Derivate Logit
Softsign
Derivate Softsign
Softplus
Logistic
Gamma
Eulersche Gamma Funktion
Lanczos Gamma-Funktion
Stirling Gamma-Funktion
Log Gamma-Funktion
Beta
Beta Funktion
Logarithmische Beta Funktion
Unvollstaendige Beta Funktion
Inverse unvollstaendige Beta Funktion
Fehlerfunktionen
erf - Fehlerfunktion
erfc - komplementäre Fehlerfunktion
Kombinatorik
Fakultät
Semifakultät
Steigende Fakultät
Fallende Fakultät
Subfakultät
Permutationen und Kombinationen
Permutation
Kombinationen
Mittlerer Binomialkoeffizient
Catalan-Zahl
Lah Zahl