Beta Funktion Rechner
Online Rechner für die Eulersche Beta-Funktion
Geben Sie die Argumente a und b ein und klicken Sie auf Berechnen um die Beta-Funktion zu ermitteln. Die Beta-Funktion ist eine fundamentale spezielle Funktion, die eng mit der Gamma-Funktion verwandt ist und in der Wahrscheinlichkeitstheorie, Kombinatorik und bei Integralproblemen eine zentrale Rolle spielt.
💡 Beta-Funktion
\(B(a,b) = \int_0^1 t^{a-1}(1-t)^{b-1} \, dt\)
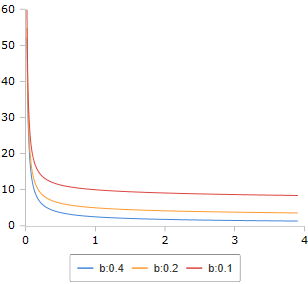
Die Beta-Funktion mit ihrer charakteristischen Integraldarstellung
Die Beta-Funktion verstehen
Die Beta-Funktion B(a,b), benannt nach Leonhard Euler, ist eine der wichtigsten speziellen Funktionen der Mathematik. Sie ist eng mit der Gamma-Funktion verwandt durch die Beziehung B(a,b) = Γ(a)Γ(b)/Γ(a+b) und tritt häufig bei Integralproblemen, Wahrscheinlichkeitsverteilungen und in der Kombinatorik auf. Die Funktion besitzt wichtige Symmetrieeigenschaften und ist fundamental für die Beta-Verteilung in der Statistik.
🧮 Grunddefinition
Integraldarstellung:
📊 Eigenschaften
- • Symmetrisch: B(a,b) = B(b,a)
- • Gamma-Relation
- • Normierungskonstante
- • Rekursionsformeln
🔬 Anwendungen
- • Beta-Verteilung
- • Binomialkoeffizienten
- • Integralrechnung
- • Bayesianische Statistik
⭐ Varianten
- • Unvollständige Beta
- • Regularisierte Beta
- • Inverse Beta
- • Logarithmische Beta
Mathematische Grundlagen
🧮 Definition und Eigenschaften
Die Beta-Funktion und ihre fundamentalen Eigenschaften:
\[\text{Integral-Definition: } B(a,b) = \int_0^1 t^{a-1}(1-t)^{b-1} \, dt \quad (a,b > 0)\] \[\text{Gamma-Beziehung: } B(a,b) = \frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)}\] \[\text{Symmetrie: } B(a,b) = B(b,a)\] \[\text{Rekursion: } B(a,b) = \frac{a-1}{a+b-1} B(a-1,b) \quad (a > 1)\]
🔄 Alternative Darstellungen
Verschiedene Integraldarstellungen der Beta-Funktion:
\[\text{Standard: } B(a,b) = \int_0^1 t^{a-1}(1-t)^{b-1} \, dt\] \[\text{Trigonometrisch: } B(a,b) = 2\int_0^{\pi/2} \sin^{2a-1}\theta \cos^{2b-1}\theta \, d\theta\] \[\text{Unendlich: } B(a,b) = \int_0^\infty \frac{u^{a-1}}{(1+u)^{a+b}} \, du\] \[\text{Symmetrisch: } B(a,b) = \int_{-\infty}^\infty \frac{e^{au}}{(1+e^u)^{a+b}} \, du\]
📊 Spezielle Werte
Wichtige Beta-Funktionswerte:
\[B(1,1) = \int_0^1 1 \, dt = 1\] \[B(1,n) = \frac{1}{n} \quad (n > 0)\] \[B(m,n) = \frac{(m-1)!(n-1)!}{(m+n-1)!} \quad (m,n \in \mathbb{N})\] \[B(1/2,1/2) = \pi\] \[B(1/2,n+1/2) = \frac{\sqrt{\pi} \Gamma(n+1/2)}{\Gamma(n+1)} = \frac{\sqrt{\pi} (2n-1)!!}{2^n n!}\]
Praktische Berechnungsbeispiele
📝 Beispiel 1: Klassische Berechnung
Aufgabe: Berechne B(2,3)
Lösung mit Integraldefinition:
\[B(2,3) = \int_0^1 t^{2-1}(1-t)^{3-1} \, dt = \int_0^1 t(1-t)^2 \, dt\] \[= \int_0^1 t(1-2t+t^2) \, dt = \int_0^1 (t - 2t^2 + t^3) \, dt\] \[= \left[\frac{t^2}{2} - \frac{2t^3}{3} + \frac{t^4}{4}\right]_0^1\] \[= \frac{1}{2} - \frac{2}{3} + \frac{1}{4} = \frac{6-8+3}{12} = \frac{1}{12}\]
Verifikation mit Gamma-Funktion:
\[B(2,3) = \frac{\Gamma(2)\Gamma(3)}{\Gamma(5)} = \frac{1! \cdot 2!}{4!} = \frac{1 \cdot 2}{24} = \frac{1}{12} \checkmark\]
📝 Beispiel 2: Binomialkoeffizienten
Aufgabe: Beziehung zu Binomialkoeffizienten
Herleitung:
\[\text{Binomialkoeffizient: } \binom{n}{k} = \frac{n!}{k!(n-k)!}\] \[\text{Beta-Funktion: } B(k+1, n-k+1) = \frac{\Gamma(k+1)\Gamma(n-k+1)}{\Gamma(n+2)}\] \[= \frac{k!(n-k)!}{(n+1)!} = \frac{k!(n-k)!}{(n+1) \cdot n!}\] \[\text{Daher: } \binom{n}{k} = \frac{1}{(n+1) \cdot B(k+1, n-k+1)}\] \[\text{Beispiel: } \binom{5}{2} = \frac{1}{6 \cdot B(3,4)} = \frac{1}{6 \cdot \frac{1}{60}} = 10\]
Anwendung: Wahrscheinlichkeitsverteilungen und Kombinatorik
📝 Beispiel 3: Beta-Verteilung
Aufgabe: Normierungskonstante der Beta-Verteilung
Wahrscheinlichkeitsdichte:
\[\text{Beta-Verteilung: } f(x|\alpha,\beta) = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)}\] \[\text{für } x \in [0,1], \alpha,\beta > 0\] \[\text{Normierung: } \int_0^1 f(x|\alpha,\beta) \, dx = 1\] \[\int_0^1 \frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)} \, dx = \frac{1}{B(\alpha,\beta)} \int_0^1 x^{\alpha-1}(1-x)^{\beta-1} \, dx\] \[= \frac{1}{B(\alpha,\beta)} \cdot B(\alpha,\beta) = 1 \checkmark\]
Bedeutung: Beta-Funktion ist essentiell für Wahrscheinlichkeitsverteilungen
Beta-Funktionen Familie
📊 Übersicht der Beta-Funktionen
| Funktion | Definition | Anwendung |
|---|---|---|
| Beta-Funktion B(a,b) |
∫₀¹ t^(a-1)(1-t)^(b-1) dt | Normierungskonstante, Kombinatorik |
| Unvollständige Beta Bₓ(a,b) |
∫₀ˣ t^(a-1)(1-t)^(b-1) dt | Kumulativeverteilungen |
| Regularisierte Beta Iₓ(a,b) |
Bₓ(a,b) / B(a,b) | Statistische Tests, p-Werte |
| Inverse Beta Iₓ⁻¹(a,b) |
x sodass Iₓ(a,b) = p | Quantile, Konfidenzintervalle |
| Log-Beta ln B(a,b) |
ln(Γ(a)) + ln(Γ(b)) - ln(Γ(a+b)) | Numerische Stabilität |
Anwendungen in verschiedenen Bereichen
📊 Wahrscheinlichkeitstheorie
- • Beta-Verteilung
- • Dirichlet-Verteilung
- • Bayesianische Konjugation
- • Prior-Verteilungen
🔢 Kombinatorik
- • Binomialkoeffizienten
- • Catalan-Zahlen
- • Stirling-Zahlen
- • Partitionen
🧮 Analysis
- • Integralrechnung
- • Spezielle Funktionen
- • Asymptotische Entwicklungen
- • Funktionalgleichungen
📈 Statistik
- • Hypothesentests
- • Konfidenzintervalle
- • ANOVA
- • Regressionsanalyse
Implementierung und Code
💻 Code-Implementierungen
Effiziente Implementierung der Beta-Funktion:
Python (SciPy):
from scipy.special import beta, betainc, betaincinv
import numpy as np
# Beta-Funktion
result = beta(a, b) # B(a,b)
incomplete = betainc(a, b, x) # Iₓ(a,b)
inverse = betaincinv(a, b, p) # Iₓ⁻¹(a,b)(p)
# Eigene Implementation
def beta_function(a, b):
"""Beta-Funktion über Gamma-Funktionen"""
from math import gamma
return gamma(a) * gamma(b) / gamma(a + b)
R:
result <- beta(a, b) # Beta-Funktion
incomplete <- pbeta(x, a, b) # Kumulativ
quantile <- qbeta(p, a, b) # Quantil
MATLAB:
result = beta(a, b); % Beta-Funktion
incomplete = betainc(x, a, b); % Unvollständig
inverse = betaincinv(p, a, b); % Invers
🎯 Numerische Implementation
Robuste Implementierung für praktische Anwendungen:
C++ (Hochpräzise):
#include <cmath>
#include <stdexcept>
double beta_function(double a, double b) {
if (a <= 0 || b <= 0) {
throw std::domain_error("Beta function: arguments must be positive");
}
// Verwende Log-Gamma für numerische Stabilität
return exp(lgamma(a) + lgamma(b) - lgamma(a + b));
}
double log_beta(double a, double b) {
"""Logarithmische Beta-Funktion für große Werte"""
return lgamma(a) + lgamma(b) - lgamma(a + b);
}
Statistische Anwendung:
def beta_distribution_pdf(x, alpha, beta):
"""Beta-Verteilung Wahrscheinlichkeitsdichte"""
if x < 0 or x > 1:
return 0
if alpha <= 0 or beta <= 0:
raise ValueError("Parameter müssen positiv sein")
# Verwende Log für numerische Stabilität
log_pdf = ((alpha - 1) * np.log(x) +
(beta - 1) * np.log(1 - x) -
log_beta(alpha, beta))
return np.exp(log_pdf)
🎯 Praktische Anwendung
Beta-Funktion in der Bayesianischen Statistik:
Bayesianische Konjugation:
def bayesian_update_beta(prior_alpha, prior_beta, successes, failures):
"""Update Beta-Prior mit neuen Daten"""
posterior_alpha = prior_alpha + successes
posterior_beta = prior_beta + failures
return posterior_alpha, posterior_beta
def beta_credible_interval(alpha, beta, confidence=0.95):
"""Bayesianisches Konfidenzintervall"""
tail_prob = (1 - confidence) / 2
lower = betaincinv(alpha, beta, tail_prob)
upper = betaincinv(alpha, beta, 1 - tail_prob)
return lower, upper
A/B Testing:
def ab_test_probability(alpha_a, beta_a, alpha_b, beta_b, n_samples=10000):
"""Monte Carlo für P(A > B) in A/B Test"""
samples_a = np.random.beta(alpha_a, beta_a, n_samples)
samples_b = np.random.beta(alpha_b, beta_b, n_samples)
return np.mean(samples_a > samples_b)
💡 Wichtige Eigenschaften der Beta-Funktion:
- Gamma-Beziehung: B(a,b) = Γ(a)Γ(b)/Γ(a+b)
- Symmetrie: B(a,b) = B(b,a)
- Normierung: Fundamentale Konstante für Beta-Verteilung
- Kombinatorik: Verbindung zu Binomialkoeffizienten
🔬 Anwendungsgebiete der Beta-Funktion:
- Wahrscheinlichkeit: Beta-Verteilung, Bayesianische Statistik
- Kombinatorik: Binomialkoeffizienten, Catalan-Zahlen
- Analysis: Integralrechnung, spezielle Funktionen
- Statistik: Hypothesentests, Konfidenzintervalle
acos - Arkuskosinus
acot - Arkuskotangens
acsc - Arkuskosekans
asec - Arkussekans
asin - Arkussinus
atan - Arkustangens
atan2 - Arkustangens von y/x
cos - Kosinus
cot - Kotangens
csc - Kosekans
sec - Sekans
sin - Sinus
sinc - Kardinalsinus
tan - Tangens
hypot - Hypotenuse
deg2rad - Grad in Radiant
rad2deg - Radiant in Grad
Hyperbolik
acosh - Arkuskosinus hyperbolikus
asinh - Areasinus hyperbolikus
atanh - Arkustangens hyperbolikus
cosh - Kosinus hyperbolikus
sinh - Sinus hyperbolikus
tanh - Tangens hyperbolikus
Logarithmus
log - Logarithmus zur angegebene Basis
ln - Natürlicher Logarithmus zur Basis e
log10 - Logarithmus zur Basis 10
log2 - Logarithmus zur Basis 2
exp - Exponenten zur Basis e
Aktivierung
Softmax
Sigmoid
Derivate Sigmoid
Logit
Derivate Logit
Softsign
Derivate Softsign
Softplus
Logistic
Gamma
Eulersche Gamma Funktion
Lanczos Gamma-Funktion
Stirling Gamma-Funktion
Log Gamma-Funktion
Beta
Beta Funktion
Logarithmische Beta Funktion
Unvollstaendige Beta Funktion
Inverse unvollstaendige Beta Funktion
Fehlerfunktionen
erf - Fehlerfunktion
erfc - komplementäre Fehlerfunktion
Kombinatorik
Fakultät
Semifakultät
Steigende Fakultät
Fallende Fakultät
Subfakultät
Permutationen und Kombinationen
Permutation
Kombinationen
Mittlerer Binomialkoeffizient
Catalan-Zahl
Lah Zahl