Logistische Funktion Rechner
Online Rechner für die logistische Sigmoid-Funktion
Geben Sie das Argument (x) ein und klicken Sie auf Berechnen um die logistische Funktion zu ermitteln. Die logistische Funktion ist eine fundamentale S-förmige Sigmoid-Kurve, die in Wachstumsmodellen, Statistik und maschinellem Lernen weit verbreitet ist.
💡 Logistische Funktion
\(\sigma(x) = \frac{1}{1 + e^{-x}}\)
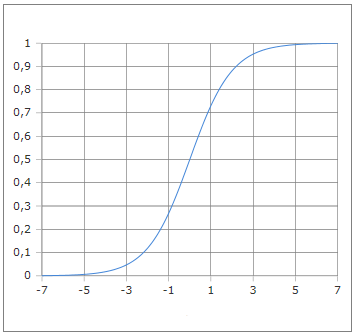
Die charakteristische S-förmige Kurve der logistischen Funktion
Die logistische Funktion verstehen
Die logistische Funktion, auch bekannt als Sigmoid-Funktion, ist eine der wichtigsten mathematischen Funktionen mit vielfältigen Anwendungen. Mit der Formel σ(x) = 1/(1+e^(-x)) erzeugt sie eine charakteristische S-förmige Kurve, die sich asymptotisch den Werten 0 und 1 nähert. Sie wird zur Modellierung begrenzten Wachstums, in der Statistik für Wahrscheinlichkeiten und im maschinellen Lernen als Aktivierungsfunktion verwendet.
📈 Grunddefinition
Mathematische Form:
📊 Eigenschaften
- • Wertebereich: (0, 1)
- • σ(0) = 0.5 (Wendepunkt)
- • Punktsymmetrie um (0, 0.5)
- • Monoton steigend
🔬 Anwendungen
- • Wachstumsmodellierung
- • Logistische Regression
- • Neuronale Netze
- • Wahrscheinlichkeitsmodelle
⭐ Vorteile
- • Begrenzte Ausgabe [0,1]
- • Überall differenzierbar
- • Einfache Ableitung
- • Probabilistische Interpretation
Mathematische Grundlagen
📈 Definition und Herleitung
Die logistische Funktion und ihre mathematischen Eigenschaften:
\[\text{Standard-Form: } \sigma(x) = \frac{1}{1 + e^{-x}}\] \[\text{Allgemeine Form: } f(x) = \frac{L}{1 + e^{-k(x-x_0)}}\] \[\text{Wobei: } L = \text{Grenzwert}, k = \text{Steigung}, x_0 = \text{Wendepunkt}\] \[\text{Inverse: } \text{logit}(p) = \ln\left(\frac{p}{1-p}\right) = \sigma^{-1}(p)\]
🔄 Ableitung und Eigenschaften
Wichtige mathematische Eigenschaften:
\[\text{Ableitung: } \sigma'(x) = \sigma(x) \cdot (1 - \sigma(x))\] \[\text{Alternative: } \sigma'(x) = \frac{e^{-x}}{(1 + e^{-x})^2}\] \[\text{Symmetrie: } \sigma(-x) = 1 - \sigma(x)\] \[\text{Wendepunkt: } \sigma(0) = 0{,}5, \quad \sigma'(0) = 0{,}25\]
📊 Charakteristische Werte
Wichtige Punkte der logistischen Funktion:
\[\text{Grenzwerte: } \lim_{x \to -\infty} \sigma(x) = 0, \quad \lim_{x \to \infty} \sigma(x) = 1\] \[\text{Wendepunkt: } x = 0 \Rightarrow \sigma(0) = 0{,}5\] \[\text{95%-Bereich: } \sigma(-3) \approx 0{,}05, \quad \sigma(3) \approx 0{,}95\] \[\text{Steiler Bereich: } x \in [-2, 2] \text{ enthält die meiste Änderung}\]
Praktische Berechnungsbeispiele
📝 Beispiel 1: Logistische Regression
Aufgabe: Wahrscheinlichkeit für binäre Klassifikation
Gegeben: Linear kombinierte Features z = 2.5
Berechnung:
\[\text{Logits: } z = w_1x_1 + w_2x_2 + b = 2{,}5\] \[\text{Wahrscheinlichkeit: } P(y=1|x) = \sigma(2{,}5) = \frac{1}{1 + e^{-2{,}5}}\] \[= \frac{1}{1 + 0{,}082} = \frac{1}{1{,}082} \approx 0{,}924\] \[\text{Klassifikation: } \hat{y} = 1 \text{ (da } P > 0{,}5\text{)}\]
Interpretation: 92.4% Wahrscheinlichkeit für Klasse 1
📝 Beispiel 2: Bevölkerungswachstum
Aufgabe: Logistisches Wachstumsmodell
Modell: P(t) = K/(1 + e^(-r(t-t₀)))
Parameter:
\[\text{Kapazität: } K = 1000 \text{ (maximale Population)}\] \[\text{Wachstumsrate: } r = 0{,}1 \text{ pro Jahr}\] \[\text{Wendepunkt: } t_0 = 10 \text{ Jahre}\] \[\text{Population nach 15 Jahren: } P(15) = \frac{1000}{1 + e^{-0{,}1(15-10)}}\] \[= \frac{1000}{1 + e^{-0{,}5}} = \frac{1000}{1 + 0{,}607} \approx 622\]
Interpretation: 622 Individuen nach 15 Jahren
📝 Beispiel 3: Neuronales Netz
Aufgabe: Aktivierungsfunktion in Ausgabeschicht
Kontext: Binäre Klassifikation
Berechnung:
\[\text{Pre-Aktivierung: } z = \sum_{i} w_i a_i + b = 1{,}2\] \[\text{Aktivierung: } a = \sigma(1{,}2) = \frac{1}{1 + e^{-1{,}2}} \approx 0{,}769\] \[\text{Ableitung für Backpropagation: } \frac{\partial a}{\partial z} = a(1-a)\] \[= 0{,}769 \times (1-0{,}769) = 0{,}769 \times 0{,}231 \approx 0{,}178\]
Gradient: Benötigt für Gewichtsaktualisierung im Training
Vor- und Nachteile
✅ Vorteile der logistischen Funktion
Positive Eigenschaften in verschiedenen Anwendungen:
\[\text{✓ Begrenzte Ausgabe zwischen 0 und 1}\] \[\text{✓ Direkte probabilistische Interpretation}\] \[\text{✓ Glatte, differenzierbare Kurve}\] \[\text{✓ Einfache Ableitung: } \sigma'(x) = \sigma(x)(1-\sigma(x))\] \[\text{✓ Numerisch stabile Implementierung möglich}\] \[\text{✓ Biologisch plausible S-Form}\]
⚠️ Nachteile und Limitationen
Herausforderungen bei der Verwendung:
\[\text{⚠ Vanishing Gradient Problem bei extremen Werten}\] \[\text{⚠ Nicht zero-centered (Ausgabe nur positiv)}\] \[\text{⚠ Sättigung bei großen |x| Werten}\] \[\text{⚠ Exponentialfunktion kann numerisch instabil sein}\] \[\text{⚠ Langsame Konvergenz in tiefen Netzen}\]
Vergleichstabelle der S-förmigen Funktionen
📊 Funktionswerte-Vergleich
| Input x | Logistic σ(x) | Tanh | Softsign | ArcTan |
|---|---|---|---|---|
| -3 | 0.047 | -0.995 | -0.750 | -1.249 |
| -1 | 0.269 | -0.762 | -0.500 | -0.785 |
| 0 | 0.500 | 0.000 | 0.000 | 0.000 |
| 1 | 0.731 | 0.762 | 0.500 | 0.785 |
| 3 | 0.953 | 0.995 | 0.750 | 1.249 |
| 5 | 0.993 | 0.999 | 0.833 | 1.373 |
Anwendungen in verschiedenen Bereichen
📊 Statistik & ML
- • Logistische Regression
- • Binäre Klassifikation
- • Wahrscheinlichkeitsmodelle
- • Generalized Linear Models
🧠 Neuronale Netze
- • Aktivierungsfunktion
- • Ausgabeschicht (binär)
- • Gating-Mechanismen
- • LSTM/GRU Tore
🔬 Wissenschaft
- • Bevölkerungsdynamik
- • Epidemiologie
- • Dose-Response Kurven
- • Psychophysik
💼 Wirtschaft
- • Marktadoption
- • Produktlebenszyklus
- • Technologie-Diffusion
- • Nachfragekurven
Implementierung und Code
💻 Code-Implementierungen
Implementierung der logistischen Funktion:
Python (NumPy):
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(x):
sig = sigmoid(x)
return sig * (1 - sig)
# Numerisch stabile Version
def stable_sigmoid(x):
return np.where(x >= 0,
1 / (1 + np.exp(-x)),
np.exp(x) / (1 + np.exp(x)))
TensorFlow/Keras:
tf.nn.sigmoid(x)
# oder als Layer:
tf.keras.activations.sigmoid
PyTorch:
torch.sigmoid(x)
# oder als Layer:
torch.nn.Sigmoid()
🎯 Praktische Anwendung
Verwendung in Machine Learning:
Logistische Regression (Scikit-learn):
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
# Daten generieren
X, y = make_classification(n_samples=1000, n_features=2)
# Modell trainieren
model = LogisticRegression()
model.fit(X, y)
# Vorhersagen (gibt Wahrscheinlichkeiten zurück)
probabilities = model.predict_proba(X)
predictions = model.predict(X)
Neuronales Netz (PyTorch):
class BinaryClassifier(nn.Module):
def __init__(self, input_size):
super().__init__()
self.linear = nn.Linear(input_size, 1)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
return self.sigmoid(self.linear(x))
# Verwendung mit BCELoss
criterion = nn.BCELoss()
🎯 Numerische Stabilität
Vermeidung von Overflow/Underflow:
Problem: exp(-x) kann für große x überlaufen
Lösung: Bedingte Implementierung
def stable_sigmoid(x):
"""
Numerisch stabile Sigmoid-Implementation
"""
# Für x >= 0: Standard-Form verwenden
# Für x < 0: Umgeformte Version verwenden
if x >= 0:
exp_neg_x = np.exp(-x)
return 1 / (1 + exp_neg_x)
else:
exp_x = np.exp(x)
return exp_x / (1 + exp_x)
# Vektorisierte Version
def vectorized_stable_sigmoid(x):
return np.where(x >= 0,
1 / (1 + np.exp(-np.clip(x, 0, 500))),
np.exp(np.clip(x, -500, 0)) / (1 + np.exp(np.clip(x, -500, 0))))
💡 Wichtige Eigenschaften der logistischen Funktion:
- S-Form: σ(x) = 1/(1+e^(-x)) - charakteristische Sigmoid-Kurve
- Wertebereich: (0, 1) - ideal für Wahrscheinlichkeiten
- Wendepunkt: Bei x=0 mit σ(0)=0.5
- Symmetrie: Punktsymmetrisch um (0, 0.5)
🔬 Anwendungsgebiete der logistischen Funktion:
- Machine Learning: Logistische Regression und binäre Klassifikation
- Neuronale Netze: Aktivierungsfunktion für Ausgabeschichten
- Statistik: Modellierung von Wahrscheinlichkeiten
- Naturwissenschaften: Wachstumsmodelle und Dose-Response-Kurven
acos - Arkuskosinus
acot - Arkuskotangens
acsc - Arkuskosekans
asec - Arkussekans
asin - Arkussinus
atan - Arkustangens
atan2 - Arkustangens von y/x
cos - Kosinus
cot - Kotangens
csc - Kosekans
sec - Sekans
sin - Sinus
sinc - Kardinalsinus
tan - Tangens
hypot - Hypotenuse
deg2rad - Grad in Radiant
rad2deg - Radiant in Grad
Hyperbolik
acosh - Arkuskosinus hyperbolikus
asinh - Areasinus hyperbolikus
atanh - Arkustangens hyperbolikus
cosh - Kosinus hyperbolikus
sinh - Sinus hyperbolikus
tanh - Tangens hyperbolikus
Logarithmus
log - Logarithmus zur angegebene Basis
ln - Natürlicher Logarithmus zur Basis e
log10 - Logarithmus zur Basis 10
log2 - Logarithmus zur Basis 2
exp - Exponenten zur Basis e
Aktivierung
Softmax
Sigmoid
Derivate Sigmoid
Logit
Derivate Logit
Softsign
Derivate Softsign
Softplus
Logistic
Gamma
Eulersche Gamma Funktion
Lanczos Gamma-Funktion
Stirling Gamma-Funktion
Log Gamma-Funktion
Beta
Beta Funktion
Logarithmische Beta Funktion
Unvollstaendige Beta Funktion
Inverse unvollstaendige Beta Funktion
Fehlerfunktionen
erf - Fehlerfunktion
erfc - komplementäre Fehlerfunktion
Kombinatorik
Fakultät
Semifakultät
Steigende Fakultät
Fallende Fakultät
Subfakultät
Permutationen und Kombinationen
Permutation
Kombinationen
Mittlerer Binomialkoeffizient
Catalan-Zahl
Lah Zahl