Logit Funktion Rechner
Online Rechner für die Umkehrfunktion der Sigmoid-Funktion
Geben Sie die Wahrscheinlichkeit (p) zwischen 0 und 1 ein und klicken Sie auf Berechnen um die Logit-Funktion zu ermitteln. Die Logit-Funktion ist die Umkehrfunktion der Sigmoid-Funktion und wandelt Wahrscheinlichkeiten in unbeschränkte reelle Zahlen um, was sie ideal für lineare Modellierung macht.
💡 Logit-Funktion
\(\text{logit}(p) = \ln\left(\frac{p}{1-p}\right) = \ln(\text{odds})\)
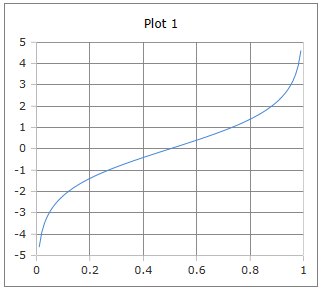
Die charakteristische Kurve der Logit-Funktion
Die Logit-Funktion verstehen
Die Logit-Funktion (auch Log-Odds-Funktion genannt) ist die Umkehrfunktion der Sigmoid-Funktion. Sie transformiert Wahrscheinlichkeiten aus dem Intervall (0,1) in unbeschränkte reelle Zahlen (-∞, +∞). Dies macht sie zur fundamentalen Link-Funktion in der logistischen Regression und ein wichtiges Werkzeug in der statistischen Modellierung.
📈 Grunddefinition
Mathematische Formen:
📊 Eigenschaften
- • Definitionsbereich: (0, 1)
- • Wertebereich: (-∞, +∞)
- • \(\text{logit}(0{,}5) = 0\)
- • Streng monoton steigend
🔬 Anwendungen
- • Logistische Regression
- • Binäre Klassifikation
- • Odds Ratio Berechnung
- • Epidemiologische Studien
⭐ Vorteile
- • Linearisiert Wahrscheinlichkeiten
- • Unbeschränkter Wertebereich
- • Symmetrisch um 0
- • Differenzierbar
Mathematische Grundlagen
📈 Verschiedene Darstellungen
Äquivalente mathematische Formulierungen:
\[\text{logit}(p) = \ln\left(\frac{p}{1-p}\right) \quad \text{(Standard-Form)}\] \[\text{logit}(p) = \ln(p) - \ln(1-p) \quad \text{(Logarithmus-Differenz)}\] \[\text{logit}(p) = -\ln\left(\frac{1}{p} - 1\right) \quad \text{(Alternative Form)}\] \[\text{logit}(p) = 2 \cdot \text{arctanh}(2p - 1) \quad \text{(Hyperbolische Form)}\]
🔄 Beziehung zur Sigmoid-Funktion
Umkehrfunktion der Sigmoid-Funktion:
\[\text{Sigmoid: } \sigma(x) = \frac{1}{1 + e^{-x}}\] \[\text{Logit: } \text{logit}(p) = \sigma^{-1}(p)\] \[\text{Verifikation: } \sigma(\text{logit}(p)) = p\] \[\text{und: } \text{logit}(\sigma(x)) = x\]
📊 Odds und Log-Odds
Konzeptuelle Grundlagen:
\[\text{Wahrscheinlichkeit: } p = P(\text{Ereignis})\] \[\text{Odds: } \text{odds} = \frac{p}{1-p} = \frac{P(\text{Ereignis})}{P(\text{Nicht-Ereignis})}\] \[\text{Log-Odds (Logit): } \text{logit}(p) = \ln(\text{odds})\] \[\text{Eigenschaften: odds} \in (0, \infty), \text{ logit} \in (-\infty, \infty)\]
Praktische Berechnungsbeispiele
📝 Beispiel 1: Klassische Wahrscheinlichkeiten
Aufgabe: Logit-Werte für typische Wahrscheinlichkeiten
Berechnung:
\[\text{logit}(0{,}1) = \ln\left(\frac{0{,}1}{0{,}9}\right) = \ln(0{,}111) \approx -2{,}197\] \[\text{logit}(0{,}5) = \ln\left(\frac{0{,}5}{0{,}5}\right) = \ln(1) = 0\] \[\text{logit}(0{,}9) = \ln\left(\frac{0{,}9}{0{,}1}\right) = \ln(9) \approx 2{,}197\] \[\text{Symmetrie: } \text{logit}(0{,}1) = -\text{logit}(0{,}9)\]
Interpretation: Symmetrische Verteilung um den Neutralpunkt 0.5
📝 Beispiel 2: Logistische Regression
Aufgabe: Modellierung einer binären Klassifikation
Szenario: Vorhersage der Bestehen-Wahrscheinlichkeit einer Prüfung
Berechnung:
\[\text{Lineare Gleichung: } \text{logit}(p) = \beta_0 + \beta_1 x_1 + \beta_2 x_2\] \[\text{Beispiel: } \text{logit}(p) = -3 + 0{,}5 \cdot \text{Lernstunden} + 0{,}3 \cdot \text{Vorerfahrung}\] \[\text{Bei 10 Stunden, Vorerfahrung 5: } \text{logit}(p) = -3 + 5 + 1{,}5 = 3{,}5\] \[\text{Wahrscheinlichkeit: } p = \sigma(3{,}5) = \frac{1}{1+e^{-3{,}5}} \approx 0{,}970\]
Interpretation: 97% Wahrscheinlichkeit für das Bestehen der Prüfung
📝 Beispiel 3: Odds Ratio Berechnung
Aufgabe: Vergleich von Behandlungsgruppen
Gegeben: Gruppe A: 80% Erfolg, Gruppe B: 60% Erfolg
Berechnung:
\[\text{Gruppe A: } \text{logit}(0{,}8) = \ln\left(\frac{0{,}8}{0{,}2}\right) = \ln(4) \approx 1{,}386\] \[\text{Gruppe B: } \text{logit}(0{,}6) = \ln\left(\frac{0{,}6}{0{,}4}\right) = \ln(1{,}5) \approx 0{,}405\] \[\text{Differenz: } 1{,}386 - 0{,}405 = 0{,}981\] \[\text{Odds Ratio: } e^{0{,}981} \approx 2{,}67\]
Interpretation: Gruppe A hat 2,67-fach höhere Odds als Gruppe B
Ableitung und mathematische Eigenschaften
📈 Ableitung der Logit-Funktion
Wichtige Ableitungseigenschaften:
\[\frac{d}{dp}\text{logit}(p) = \frac{d}{dp}\ln\left(\frac{p}{1-p}\right)\] \[= \frac{1-p}{p} \cdot \frac{1 \cdot (1-p) - p \cdot (-1)}{(1-p)^2}\] \[= \frac{1-p}{p} \cdot \frac{1}{(1-p)^2} = \frac{1}{p(1-p)}\] \[\text{Minimum bei } p = 0{,}5: \frac{d\text{logit}}{dp}\Big|_{p=0{,}5} = 4\]
🔄 Grenzwertverhalten
Verhalten an den Rändern des Definitionsbereichs:
\[\lim_{p \to 0^+} \text{logit}(p) = \lim_{p \to 0^+} \ln\left(\frac{p}{1-p}\right) = -\infty\] \[\lim_{p \to 1^-} \text{logit}(p) = \lim_{p \to 1^-} \ln\left(\frac{p}{1-p}\right) = +\infty\] \[\text{logit}(0{,}5) = 0 \quad \text{(Neutralpunkt)}\] \[\text{Symmetrie: } \text{logit}(1-p) = -\text{logit}(p)\]
Anwendungen in verschiedenen Bereichen
📊 Statistik & Data Science
- • Logistische Regression
- • Generalisierte lineare Modelle
- • Binäre Klassifikation
- • A/B-Testing Analyse
🧠 Machine Learning
- • Preprocessing für Sigmoid
- • Feature Engineering
- • Calibration von Modellen
- • Ensemble-Methoden
🏥 Medizin & Epidemiologie
- • Risikofaktor-Analyse
- • Odds Ratio Berechnung
- • Klinische Studien
- • Diagnosevorhersage
💼 Wirtschaft & Finance
- • Kreditrisikobewertung
- • Marktforschung
- • Kundenverhalten-Analyse
- • Investitionsentscheidungen
Implementierung und Code
💻 Code-Implementierungen
Numerisch stabile Implementierungen:
Python (NumPy):
import numpy as np
def logit(p):
# Numerisch stabile Version
return np.log(p / (1 - p))
def safe_logit(p, eps=1e-7):
# Mit Clipping für numerische Stabilität
p_clipped = np.clip(p, eps, 1-eps)
return np.log(p_clipped / (1 - p_clipped))
SciPy:
from scipy.special import logit
result = logit(0.75) # Built-in Funktion
R:
logit <- qlogis # Built-in Funktion
# oder selbst implementiert:
logit <- function(p) log(p/(1-p))
📊 Logistische Regression in Python
Praktische Implementierung mit sklearn:
Logistische Regression:
from sklearn.linear_model import LogisticRegression
import numpy as np
# Modell trainieren
model = LogisticRegression()
model.fit(X, y)
# Logit-Werte (log-odds) vorhersagen
logits = model.decision_function(X_new)
# In Wahrscheinlichkeiten umwandeln
probabilities = 1 / (1 + np.exp(-logits))
# oder direkt:
probabilities = model.predict_proba(X_new)[:, 1]
# Odds ratio berechnen
odds_ratio = np.exp(model.coef_[0])
⚡ Numerische Überlegungen
Wichtige Punkte für die Implementierung:
\[\text{Problem: } p = 0 \text{ oder } p = 1 \Rightarrow \text{logit nicht definiert}\] \[\text{Lösung: Clipping mit } \epsilon: p \in [\epsilon, 1-\epsilon]\] \[\text{Typisch: } \epsilon = 10^{-7} \text{ oder } 10^{-15}\] \[\text{Alternative: Regulierung in der Verlustfunktion}\]
Probleme und Lösungsansätze
⚠️ Numerische Instabilität
Herausforderungen bei extremen Wahrscheinlichkeiten:
\[\text{Problem: } p \to 0 \text{ oder } p \to 1 \Rightarrow \text{logit} \to \pm\infty\] \[\text{Floating-Point-Fehler bei } p \approx 0 \text{ oder } p \approx 1\] \[\text{Lösung 1: Clipping } p \in [\epsilon, 1-\epsilon]\] \[\text{Lösung 2: Regularisierung in Verlustfunktion}\] \[\text{Lösung 3: Alternative Parametrisierung}\]
💡 Wichtige Eigenschaften der Logit-Funktion:
- Linearisierung: Wandelt beschränkte Wahrscheinlichkeiten in unbeschränkte Werte um
- Symmetrie: logit(1-p) = -logit(p) um den Neutralpunkt 0.5
- Link-Funktion: Ermöglicht lineare Modellierung von Wahrscheinlichkeiten
- Interpretierbarkeit: Direkte Verbindung zu Odds und Odds Ratios
🔬 Anwendungsgebiete der Logit-Funktion:
- Statistik: Logistische Regression, generalisierte lineare Modelle
- Machine Learning: Binäre Klassifikation, Feature Engineering
- Medizin: Risikobewertung, epidemiologische Studien
- Wirtschaft: Kreditrisiko, Marktanalyse, Kundenverhalten
acos - Arkuskosinus
acot - Arkuskotangens
acsc - Arkuskosekans
asec - Arkussekans
asin - Arkussinus
atan - Arkustangens
atan2 - Arkustangens von y/x
cos - Kosinus
cot - Kotangens
csc - Kosekans
sec - Sekans
sin - Sinus
sinc - Kardinalsinus
tan - Tangens
hypot - Hypotenuse
deg2rad - Grad in Radiant
rad2deg - Radiant in Grad
Hyperbolik
acosh - Arkuskosinus hyperbolikus
asinh - Areasinus hyperbolikus
atanh - Arkustangens hyperbolikus
cosh - Kosinus hyperbolikus
sinh - Sinus hyperbolikus
tanh - Tangens hyperbolikus
Logarithmus
log - Logarithmus zur angegebene Basis
ln - Natürlicher Logarithmus zur Basis e
log10 - Logarithmus zur Basis 10
log2 - Logarithmus zur Basis 2
exp - Exponenten zur Basis e
Aktivierung
Softmax
Sigmoid
Derivate Sigmoid
Logit
Derivate Logit
Softsign
Derivate Softsign
Softplus
Logistic
Gamma
Eulersche Gamma Funktion
Lanczos Gamma-Funktion
Stirling Gamma-Funktion
Log Gamma-Funktion
Beta
Beta Funktion
Logarithmische Beta Funktion
Unvollstaendige Beta Funktion
Inverse unvollstaendige Beta Funktion
Fehlerfunktionen
erf - Fehlerfunktion
erfc - komplementäre Fehlerfunktion
Kombinatorik
Fakultät
Semifakultät
Steigende Fakultät
Fallende Fakultät
Subfakultät
Permutationen und Kombinationen
Permutation
Kombinationen
Mittlerer Binomialkoeffizient
Catalan-Zahl
Lah Zahl