Komplementäre Fehlerfunktion Erfc Rechner
Online Berechnung der Complementary Error Function für Statistik und Physik
Geben Sie das Argument x ein und klicken Sie auf Berechnen um die komplementäre Fehlerfunktion zu ermitteln. Die komplementäre Fehlerfunktion erfc(x) ist eine wichtige mathematische Funktion in der Statistik, Physik und Wahrscheinlichkeitstheorie, die die Wahrscheinlichkeit außerhalb eines bestimmten Bereichs in der Normalverteilung beschreibt.
💡 Komplementäre Fehlerfunktion
\(\text{erfc}(x) = 1 - \text{erf}(x) = \frac{2}{\sqrt{\pi}} \int_x^\infty e^{-t^2} \, dt\)
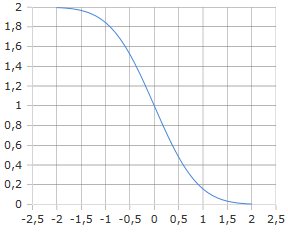
Charakteristische abfallende Kurve der komplementären Fehlerfunktion
Die komplementäre Fehlerfunktion verstehen
Die komplementäre Fehlerfunktion (englisch: complementary error function, abgekürzt als erfc) ist eine mathematische Funktion, die eng mit der Fehlerfunktion erf(x) verknüpft ist und in Statistik, Physik und Technik häufig verwendet wird. Sie misst die Fläche unter der Kurve der Gauß-Funktion ab x bis unendlich und gibt die Wahrscheinlichkeit an, dass ein Wert außerhalb eines bestimmten Bereichs liegt.
📈 Definition
Mathematische Formen:
📊 Eigenschaften
- • erfc(0) = 1
- • erfc(∞) = 0, erfc(-∞) = 2
- • Monoton fallend
- • Wertebereich: [0, 2]
- • Für negative x ist erfc(x) > 1
🔬 Anwendungen
- • Tail-Wahrscheinlichkeiten
- • Signalverarbeitung
- • Wärmeleitungsgleichung
- • Diffusionsprozesse
⭐ Beziehungen
- • erfc(x) = 1 - erf(x)
- • erf(x) + erfc(x) = 1
- • erfc(-x) = 2 - erfc(x)
- • P(X > x) = ½ erfc(x/√2)
Mathematische Eigenschaften
📈 Grundlegende Eigenschaften
Wichtige mathematische Eigenschaften der komplementären Fehlerfunktion:
\[\text{Definition: } \text{erfc}(x) = 1 - \text{erf}(x) = \frac{2}{\sqrt{\pi}} \int_x^\infty e^{-t^2} \, dt\] \[\text{Komplementarität: } \text{erf}(x) + \text{erfc}(x) = 1\] \[\text{Grenzwerte: } \text{erfc}(0) = 1, \quad \text{erfc}(\infty) = 0, \quad \text{erfc}(-\infty) = 2\] \[\text{Symmetrieeigenschaft: } \text{erfc}(-x) = 2 - \text{erfc}(x)\] \[\text{Ableitung: } \frac{d}{dx}\text{erfc}(x) = -\frac{2}{\sqrt{\pi}} e^{-x^2}\]
🔄 Verbindung zur Normalverteilung
Tail-Wahrscheinlichkeiten und Überlebensfunktionen:
\[\text{Tail-Wahrscheinlichkeit: } P(X > x) = \frac{1}{2}\text{erfc}\left(\frac{x}{\sqrt{2}}\right) \text{ für } X \sim N(0,1)\] \[\text{Allgemeine Normalverteilung: } P(X > x) = \frac{1}{2}\text{erfc}\left(\frac{x-\mu}{\sigma\sqrt{2}}\right)\] \[\text{Signifikanzgrenze: } \alpha = P(|Z| > z_{\alpha/2}) = \text{erfc}\left(\frac{z_{\alpha/2}}{\sqrt{2}}\right)\] \[\text{Q-Funktion: } Q(x) = \frac{1}{2}\text{erfc}\left(\frac{x}{\sqrt{2}}\right)\]
📊 Wichtige Werte
Häufig verwendete Funktionswerte:
\[\text{erfc}(0) = 1\] \[\text{erfc}(0{,}5) \approx 0{,}4795\] \[\text{erfc}(1) \approx 0{,}1573\] \[\text{erfc}(\sqrt{2}) \approx 0{,}0455 \text{ (2σ-Tail)}\] \[\text{erfc}(2) \approx 0{,}0047\] \[\text{erfc}(3) \approx 0{,}0000221\]
Praktische Anwendungsbeispiele
📝 Beispiel 1: Tail-Wahrscheinlichkeit
Aufgabe: Wahrscheinlichkeit für extreme Werte
Gegeben: X ~ N(0,1), gesucht P(X > 2)
Berechnung:
\[P(X > 2) = \frac{1}{2}\text{erfc}\left(\frac{2}{\sqrt{2}}\right)\] \[\text{erfc}(\sqrt{2}) = \text{erfc}(1{,}414) \approx 0{,}0455\] \[P(X > 2) = \frac{1}{2} \times 0{,}0455 = 0{,}0228\]
Interpretation: Nur 2,28% der Werte liegen über 2 bei der Standardnormalverteilung
📝 Beispiel 2: Signalverarbeitung
Aufgabe: Bit-Fehlerrate bei digitaler Übertragung
Szenario: BPSK-Modulation mit Rauschen
Berechnung:
\[\text{Bit-Fehlerrate: } P_e = \frac{1}{2}\text{erfc}\left(\sqrt{\frac{E_b}{N_0}}\right)\] \[\text{Für } \frac{E_b}{N_0} = 4 \text{ (6 dB): } P_e = \frac{1}{2}\text{erfc}(\sqrt{4}) = \frac{1}{2}\text{erfc}(2)\] \[P_e = \frac{1}{2} \times 0{,}0047 \approx 2{,}3 \times 10^{-3}\]
Anwendung: Qualitätsbewertung digitaler Kommunikationssysteme
📝 Beispiel 3: Temperaturkontrolle
Aufgabe: Wahrscheinlichkeit für Überhitzung
Gegeben: Temperatur T ~ N(20°C, 3°C), kritisch > 27°C
Berechnung:
\[P(T > 27) = P\left(\frac{T-20}{3} > \frac{27-20}{3}\right) = P(Z > 2{,}33)\] \[= \frac{1}{2}\text{erfc}\left(\frac{2{,}33}{\sqrt{2}}\right) = \frac{1}{2}\text{erfc}(1{,}65)\] \[\approx \frac{1}{2} \times 0{,}0099 = 0{,}0049\]
Bedeutung: Nur 0,49% Wahrscheinlichkeit für kritische Überhitzung
Anwendungen in verschiedenen Bereichen
📊 Statistik
- • Tail-Wahrscheinlichkeiten
- • Überlebensfunktionen
- • Extreme Value Analysis
- • Signifikanztests
📡 Signalverarbeitung
- • Bit-Fehlerrate (BER)
- • Q-Funktion
- • Kommunikationssysteme
- • Rauschanalyse
🔬 Physik
- • Diffusionsprozesse
- • Wärmeleitungstheorie
- • Quantenmechanik
- • Plasma-Physik
⚙️ Ingenieurswesen
- • Zuverlässigkeitsanalyse
- • Qualitätskontrolle
- • Risikobewertung
- • Regelungstechnik
Implementierung und Code
💻 Code-Implementierungen
Effiziente Implementierung der komplementären Fehlerfunktion:
Python (SciPy/Math):
import math
from scipy.special import erfc, erf
import numpy as np
# Komplementäre Fehlerfunktion
result = math.erfc(x) # Built-in seit Python 3.2
result = erfc(x) # SciPy Version
# Alternative Berechnung
result = 1 - math.erf(x)
# Anwendung: Tail-Wahrscheinlichkeit
def tail_probability(x, mu=0, sigma=1):
"""P(X > x) für Normalverteilung"""
return 0.5 * erfc((x - mu) / (sigma * np.sqrt(2)))
# Beispiel: P(X > 2) bei N(0,1)
prob = tail_probability(2, 0, 1)
print(f"P(X > 2) = {prob:.6f}")
R:
# R implementierung
erfc <- function(x) 1 - erf(x)
# Oder direkt:
erfc <- function(x) 2 * pnorm(-x * sqrt(2))
MATLAB:
result = erfc(x); % Built-in Funktion
% Tail-Wahrscheinlichkeit:
tail_prob = @(x, mu, sigma) 0.5 * erfc((x - mu) / (sigma * sqrt(2)));
🎯 Signalverarbeitungs-Toolkit
BER-Berechnung für Kommunikationssysteme:
Python Kommunikations-Toolkit:
import math
import numpy as np
class DigitalCommunication:
def __init__(self):
pass
def bpsk_ber(self, eb_n0_db):
"""Bit-Fehlerrate für BPSK"""
eb_n0 = 10**(eb_n0_db / 10) # dB to linear
return 0.5 * math.erfc(math.sqrt(eb_n0))
def qpsk_ber(self, eb_n0_db):
"""Bit-Fehlerrate für QPSK"""
eb_n0 = 10**(eb_n0_db / 10)
return 0.5 * math.erfc(math.sqrt(eb_n0))
def awgn_capacity(self, snr_db):
"""Shannon-Kapazität für AWGN-Kanal"""
snr = 10**(snr_db / 10)
return math.log2(1 + snr)
def q_function(self, x):
"""Q-Funktion basierend auf erfc"""
return 0.5 * math.erfc(x / math.sqrt(2))
# Beispiel
comm = DigitalCommunication()
ber_6db = comm.bpsk_ber(6) # BER bei 6 dB
print(f"BPSK BER @ 6dB: {ber_6db:.2e}")
print(f"Q(2): {comm.q_function(2):.6f}")
🎯 Approximationen
Numerische Approximationen für verschiedene Bereiche:
Python Approximationen:
import math
def erfc_approx_large_x(x):
"""Asymptotische Entwicklung für große x"""
if x < 4:
return math.erfc(x) # Use exact for small x
# Asymptotische Reihe
exp_neg_x2 = math.exp(-x*x)
sqrt_pi_x = math.sqrt(math.pi) * x
# Erste Terme der asymptotischen Reihe
term1 = 1
term2 = -1 / (2 * x * x)
term3 = 3 / (4 * x**4)
return exp_neg_x2 / sqrt_pi_x * (term1 + term2 + term3)
def erfc_bounds(x):
"""Ober- und Untergrenzen für erfc"""
if x <= 0:
return math.erfc(x), math.erfc(x)
exp_neg_x2 = math.exp(-x*x)
sqrt_pi = math.sqrt(math.pi)
# Chernoff-Grenze (Obergrenze)
upper = exp_neg_x2
# Asymptotische Untergrenze
lower = exp_neg_x2 / (sqrt_pi * x * (1 + 1/(2*x*x)))
return lower, upper
# Vergleich
x = 3.0
exact = math.erfc(x)
approx = erfc_approx_large_x(x)
lower, upper = erfc_bounds(x)
print(f"Exakt: {exact:.8f}")
print(f"Approximation: {approx:.8f}")
print(f"Grenzen: [{lower:.8f}, {upper:.8f}]")
💡 Wichtige Eigenschaften der komplementären Fehlerfunktion:
- Komplementarität: erfc(x) = 1 - erf(x), beide addieren sich zu 1
- Tail-Funktion: Misst Wahrscheinlichkeiten in den Rändern
- Monotonie: Streng monoton fallend
- Asymptotik: Exponentiell abfallend für große x
🔬 Anwendungsgebiete der komplementären Fehlerfunktion:
- Statistik: Tail-Wahrscheinlichkeiten, Überlebensfunktionen, Extreme Value Analysis
- Signalverarbeitung: Bit-Fehlerrate, Q-Funktion, Kommunikationstechnik
- Physik: Diffusionsprozesse, Wärmeleitung, Quantenmechanik
- Ingenieurswesen: Zuverlässigkeitsanalyse, Qualitätskontrolle, Risikobewertung
acos - Arkuskosinus
acot - Arkuskotangens
acsc - Arkuskosekans
asec - Arkussekans
asin - Arkussinus
atan - Arkustangens
atan2 - Arkustangens von y/x
cos - Kosinus
cot - Kotangens
csc - Kosekans
sec - Sekans
sin - Sinus
sinc - Kardinalsinus
tan - Tangens
hypot - Hypotenuse
deg2rad - Grad in Radiant
rad2deg - Radiant in Grad
Hyperbolik
acosh - Arkuskosinus hyperbolikus
asinh - Areasinus hyperbolikus
atanh - Arkustangens hyperbolikus
cosh - Kosinus hyperbolikus
sinh - Sinus hyperbolikus
tanh - Tangens hyperbolikus
Logarithmus
log - Logarithmus zur angegebene Basis
ln - Natürlicher Logarithmus zur Basis e
log10 - Logarithmus zur Basis 10
log2 - Logarithmus zur Basis 2
exp - Exponenten zur Basis e
Aktivierung
Softmax
Sigmoid
Derivate Sigmoid
Logit
Derivate Logit
Softsign
Derivate Softsign
Softplus
Logistic
Gamma
Eulersche Gamma Funktion
Lanczos Gamma-Funktion
Stirling Gamma-Funktion
Log Gamma-Funktion
Beta
Beta Funktion
Logarithmische Beta Funktion
Unvollstaendige Beta Funktion
Inverse unvollstaendige Beta Funktion
Fehlerfunktionen
erf - Fehlerfunktion
erfc - komplementäre Fehlerfunktion
Kombinatorik
Fakultät
Semifakultät
Steigende Fakultät
Fallende Fakultät
Subfakultät
Permutationen und Kombinationen
Permutation
Kombinationen
Mittlerer Binomialkoeffizient
Catalan-Zahl
Lah Zahl