Sigmoid Funktion Rechner
Online Rechner für die logistische Aktivierungsfunktion
Geben Sie das Argument (t) ein und klicken Sie auf Berechnen um die Sigmoid-Funktion zu ermitteln. Die Sigmoid-Funktion ist eine S-förmige Kurve, die jeden reellen Wert auf das Intervall (0,1) abbildet und eine der klassischen Aktivierungsfunktionen in neuronalen Netzen ist.
💡 Sigmoid-Funktion
\(\sigma(t) = \frac{1}{1 + e^{-t}} = \frac{e^t}{1 + e^t}\)
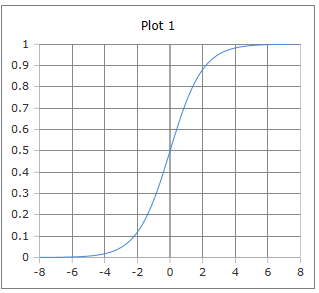
Die charakteristische S-förmige Kurve der Sigmoid-Funktion
Die Sigmoid-Funktion verstehen
Die Sigmoid-Funktion (auch logistische Funktion genannt) ist eine der wichtigsten Aktivierungsfunktionen in Machine Learning und neuronalen Netzen. Sie zeichnet sich durch ihre charakteristische S-förmige Kurve aus und bildet jeden reellen Wert auf das Intervall (0,1) ab, was sie ideal für binäre Klassifikation und als Wahrscheinlichkeitsschätzer macht.
📈 Grunddefinition
Mathematische Formen:
📊 Eigenschaften
- • Wertebereich: (0, 1)
- • \(\sigma(0) = 0{,}5\)
- • Differenzierbar
- • Monoton steigend
🔬 Anwendungen
- • Binäre Klassifikation
- • Logistische Regression
- • Neuronale Netze (klassisch)
- • Wahrscheinlichkeitsschätzung
⭐ Vorteile
- • Glatte, differenzierbare Funktion
- • Ausgabe zwischen 0 und 1
- • Interpretierbar als Wahrscheinlichkeit
- • Einfache Ableitung
Mathematische Grundlagen
📈 Verschiedene Darstellungen
Äquivalente mathematische Formulierungen:
\[\sigma(t) = \frac{1}{1 + e^{-t}} \quad \text{(Standard-Form)}\] \[\sigma(t) = \frac{e^t}{1 + e^t} \quad \text{(Alternative Form)}\] \[\sigma(t) = \frac{1}{2} \left(1 + \tanh\left(\frac{t}{2}\right)\right) \quad \text{(Tanh-Form)}\] \[\sigma(t) = \frac{1}{2} + \frac{1}{4}\text{sech}^2\left(\frac{t}{2}\right) \quad \text{(Ableitung von Tanh)}\]
🔄 Wichtige Eigenschaften
Fundamentale mathematische Eigenschaften:
\[\text{Symmetrie: } \sigma(-t) = 1 - \sigma(t)\] \[\text{Nullpunkt: } \sigma(0) = 0{,}5\] \[\text{Grenzwerte: } \lim_{t \to -\infty} \sigma(t) = 0, \quad \lim_{t \to +\infty} \sigma(t) = 1\] \[\text{Umkehrfunktion: } \sigma^{-1}(p) = \ln\left(\frac{p}{1-p}\right) \quad \text{(Logit)}\]
📊 Ableitung und Analysis
Wichtige Ableitungseigenschaften:
\[\frac{d\sigma}{dt} = \sigma(t) \cdot (1 - \sigma(t)) \quad \text{(Elegante Form)}\] \[\frac{d\sigma}{dt} = \frac{e^{-t}}{(1 + e^{-t})^2} \quad \text{(Direkte Form)}\] \[\text{Maximum der Ableitung bei } t = 0: \quad \frac{d\sigma}{dt}\Big|_{t=0} = \frac{1}{4}\] \[\text{Wendepunkt bei } t = 0\]
Praktische Berechnungsbeispiele
📝 Beispiel 1: Klassische Werte
Aufgabe: Sigmoid-Werte für wichtige Punkte
Berechnung:
\[\sigma(-2) = \frac{1}{1 + e^{2}} = \frac{1}{1 + 7{,}389} \approx 0{,}119 \quad (11{,}9\%)\] \[\sigma(0) = \frac{1}{1 + e^{0}} = \frac{1}{1 + 1} = 0{,}5 \quad (50\%)\] \[\sigma(2) = \frac{1}{1 + e^{-2}} = \frac{1}{1 + 0{,}135} \approx 0{,}881 \quad (88{,}1\%)\]
Symmetrie: σ(-2) + σ(2) = 0.119 + 0.881 = 1 ✓
📝 Beispiel 2: Logistische Regression
Aufgabe: Binäre Klassifikation mit Sigmoid
Szenario: Spam-Erkennung mit linearem Modell
Berechnung:
\[\text{Lineares Modell: } z = w_0 + w_1 x_1 + w_2 x_2\] \[\text{Beispiel: } z = -2 + 3 \cdot 0{,}8 + 1{,}5 \cdot 0{,}6 = -2 + 2{,}4 + 0{,}9 = 1{,}3\] \[P(\text{Spam}) = \sigma(1{,}3) = \frac{1}{1 + e^{-1{,}3}} \approx 0{,}786\] \[\text{Klassifikation: } P > 0{,}5 \Rightarrow \text{Spam} (78{,}6\%) \text{Wahrscheinlichkeit}\]
Interpretation: Hohe Wahrscheinlichkeit für Spam-Klassifikation
📝 Beispiel 3: Neuronales Netzwerk
Aufgabe: Aktivierung in versteckter Schicht
Gegeben: Eingaben [0.5, 0.8], Gewichte [0.3, 0.7], Bias -0.2
Berechnung:
\[\text{Net-Input: } z = \sum w_i x_i + b = 0{,}3 \cdot 0{,}5 + 0{,}7 \cdot 0{,}8 - 0{,}2\] \[z = 0{,}15 + 0{,}56 - 0{,}2 = 0{,}51\] \[\text{Aktivierung: } a = \sigma(0{,}51) = \frac{1}{1 + e^{-0{,}51}} \approx 0{,}625\] \[\text{Ableitung: } \sigma'(0{,}51) = 0{,}625 \cdot (1 - 0{,}625) = 0{,}234\]
Backpropagation: Die Ableitung wird für Gradientenberechnung benötigt
Sigmoid vs. andere Aktivierungsfunktionen
📊 Vergleichstabelle
| Input | Sigmoid | Tanh | ReLU | Verwendung |
|---|---|---|---|---|
| -2 | 0.119 | -0.964 | 0 | Negative Eingaben |
| 0 | 0.5 | 0 | 0 | Neutraler Punkt |
| 1 | 0.731 | 0.762 | 1 | Moderate Aktivierung |
| 2 | 0.881 | 0.964 | 2 | Starke Aktivierung |
| 5 | 0.993 | 0.999 | 5 | Sättigung bei Sigmoid/Tanh |
Probleme und Lösungen
⚠️ Vanishing Gradient Problem
Hauptproblem der Sigmoid-Funktion in tiefen Netzen:
\[\text{Problem: } \frac{d\sigma}{dt} = \sigma(t)(1-\sigma(t)) \leq \frac{1}{4}\] \[\text{Bei } |t| > 3: \quad \frac{d\sigma}{dt} < 0{,}05 \quad \text{(sehr kleine Gradienten)}\] \[\text{Ketten-Multiplikation: } \prod_{i=1}^{n} \sigma'_i < \left(\frac{1}{4}\right)^n \quad \text{(exponentieller Zerfall)}\] \[\text{Lösung: ReLU, Residual Connections, Batch Normalization}\]
🎯 Moderne Alternativen
Warum andere Aktivierungsfunktionen bevorzugt werden:
\[\text{ReLU: } f(x) = \max(0, x) \quad \text{(keine Sättigung, einfach)}\] \[\text{Swish: } f(x) = x \cdot \sigma(x) \quad \text{(smooth, selbst-gated)}\] \[\text{GELU: } f(x) = x \cdot \Phi(x) \quad \text{(probabilistische Interpretation)}\] \[\text{Verwendung heute: Output-Layer für binäre Klassifikation}\]
Anwendungen in verschiedenen Bereichen
🧠 Machine Learning
- • Logistische Regression
- • Binäre Klassifikation
- • Output-Layer (Wahrscheinlichkeiten)
- • Klassische neuronale Netze
📊 Statistik
- • Logit-Modelle
- • Odds Ratio Berechnungen
- • Binäre Regressionsanalyse
- • Wahrscheinlichkeitsmodellierung
🏥 Medizin & Biologie
- • Dosis-Wirkungs-Kurven
- • Epidemiologische Modelle
- • Risikobewertung
- • Populationsdynamik
💼 Wirtschaft
- • Marktanteilsmodelle
- • Kreditrisikobewertung
- • Adoptionskurven
- • Kaufwahrscheinlichkeiten
Implementierung und Code
💻 Code-Implementierungen
Numerisch stabile Implementierungen:
Python (NumPy):
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# Numerisch stabil für große |x|:
def stable_sigmoid(x):
return np.where(x >= 0,
1 / (1 + np.exp(-x)),
np.exp(x) / (1 + np.exp(x)))
TensorFlow/Keras:
tf.nn.sigmoid(x)
# oder als Layer:
tf.keras.activations.sigmoid
PyTorch:
torch.sigmoid(x)
# oder
torch.nn.Sigmoid()
📈 Ableitung implementieren
Effiziente Berechnung der Sigmoid-Ableitung:
Python Implementation:
def sigmoid_derivative(x):
s = sigmoid(x)
return s * (1 - s)
# Oder wenn sigmoid bereits berechnet:
def sigmoid_derivative_from_output(sigmoid_output):
return sigmoid_output * (1 - sigmoid_output)
# Für Backpropagation verwenden:
gradient = error * sigmoid_derivative_from_output(activation)
💡 Wichtige Eigenschaften der Sigmoid-Funktion:
- S-förmige Kurve: Charakteristische Form mit sanften Übergängen
- Wertebereich (0,1): Ideal für Wahrscheinlichkeitsinterpretation
- Differenzierbar: Glatte Funktion ermöglicht Gradientenverfahren
- Historisch wichtig: Grundlage für frühe neuronale Netze
🔬 Anwendungsgebiete der Sigmoid-Funktion:
- Machine Learning: Binäre Klassifikation, logistische Regression
- Neuronale Netze: Output-Layer für Wahrscheinlichkeiten
- Statistik: Logit-Modelle, Odds Ratio Berechnungen
- Biologie/Medizin: Dosis-Wirkungs-Kurven, Wachstumsmodelle
acos - Arkuskosinus
acot - Arkuskotangens
acsc - Arkuskosekans
asec - Arkussekans
asin - Arkussinus
atan - Arkustangens
atan2 - Arkustangens von y/x
cos - Kosinus
cot - Kotangens
csc - Kosekans
sec - Sekans
sin - Sinus
sinc - Kardinalsinus
tan - Tangens
hypot - Hypotenuse
deg2rad - Grad in Radiant
rad2deg - Radiant in Grad
Hyperbolik
acosh - Arkuskosinus hyperbolikus
asinh - Areasinus hyperbolikus
atanh - Arkustangens hyperbolikus
cosh - Kosinus hyperbolikus
sinh - Sinus hyperbolikus
tanh - Tangens hyperbolikus
Logarithmus
log - Logarithmus zur angegebene Basis
ln - Natürlicher Logarithmus zur Basis e
log10 - Logarithmus zur Basis 10
log2 - Logarithmus zur Basis 2
exp - Exponenten zur Basis e
Aktivierung
Softmax
Sigmoid
Derivate Sigmoid
Logit
Derivate Logit
Softsign
Derivate Softsign
Softplus
Logistic
Gamma
Eulersche Gamma Funktion
Lanczos Gamma-Funktion
Stirling Gamma-Funktion
Log Gamma-Funktion
Beta
Beta Funktion
Logarithmische Beta Funktion
Unvollstaendige Beta Funktion
Inverse unvollstaendige Beta Funktion
Fehlerfunktionen
erf - Fehlerfunktion
erfc - komplementäre Fehlerfunktion
Kombinatorik
Fakultät
Semifakultät
Steigende Fakultät
Fallende Fakultät
Subfakultät
Permutationen und Kombinationen
Permutation
Kombinationen
Mittlerer Binomialkoeffizient
Catalan-Zahl
Lah Zahl