Softplus Funktion Rechner
Online Rechner für die Softplus-Aktivierungsfunktion
Geben Sie das Argument (x) ein und klicken Sie auf Berechnen um die Softplus-Funktion zu ermitteln. Die Softplus-Funktion ist eine glatte Alternative zur ReLU-Funktion mit kontinuierlichen Ableitungen und immer positiven Ausgabewerten.
💡 Softplus-Funktion
\(\text{softplus}(x) = \ln(1 + e^x)\)
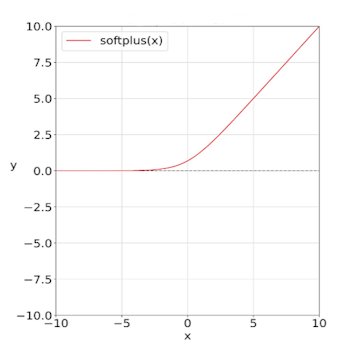
Die glatte Kurve der Softplus-Funktion als Alternative zu ReLU
Die Softplus-Funktion verstehen
Die Softplus-Funktion ist eine glatte, differenzierbare Alternative zur ReLU-Funktion, die in neuronalen Netzen und beim maschinellen Lernen eingesetzt wird. Mit der Formel softplus(x) = ln(1+e^x) bietet sie überall kontinuierliche Ableitungen und ist immer positiv. Sie approximiert die ReLU-Funktion sehr gut, löst aber das Problem der nicht-differenzierbaren Stelle bei x=0.
🌟 Grunddefinition
Mathematische Form:
📈 Eigenschaften
- • Wertebereich: (0, ∞)
- • softplus(0) = ln(2) ≈ 0.693
- • Überall differenzierbar
- • Approximiert ReLU für große x
🔬 Anwendungen
- • Alternative zu ReLU
- • Variational Autoencoders
- • Probabilistische Modelle
- • Gaußsche Aktivierungen
⭐ Vorteile
- • Überall differenzierbar
- • Immer positive Ausgabe
- • Glatte Übergänge
- • Numerisch stabil
Mathematische Grundlagen
🌟 Definition und Herleitung
Die Softplus-Funktion als glatte ReLU-Approximation:
\[\text{ReLU}(x) = \max(0, x) = \begin{cases} x & \text{wenn } x > 0 \\ 0 & \text{wenn } x \leq 0 \end{cases}\] \[\text{Softplus}(x) = \ln(1 + e^x) \quad \text{(glatte Approximation)}\] \[\text{Beziehung: } \lim_{x \to \infty} [\text{softplus}(x) - x] = 0\] \[\text{Ableitung: } \frac{d}{dx}\text{softplus}(x) = \frac{e^x}{1 + e^x} = \sigma(x)\]
🔄 Vergleich mit ReLU
Softplus vs. ReLU-Funktion:
\[\text{ReLU: Nicht differenzierbar bei } x = 0\] \[\text{Softplus: Überall differenzierbar}\] \[\text{Für große } x: \text{softplus}(x) \approx \text{ReLU}(x) + \ln(2)\] \[\text{Für } x = 0: \text{ReLU}(0) = 0, \quad \text{softplus}(0) = \ln(2) \approx 0{,}693\] \[\text{Glättungsparameter: } \text{softplus}(x) = \frac{1}{\beta}\ln(1 + e^{\beta x})\]
📊 Wichtige Eigenschaften
Charakteristische Werte und Verhalten:
\[\text{Wertebereich: } (0, \infty) \text{ - immer positiv}\] \[\text{Monoton steigend: } \text{softplus}'(x) = \sigma(x) > 0\] \[\text{Konvex: } \text{softplus}''(x) = \sigma(x)(1-\sigma(x)) \geq 0\] \[\text{Asymptotik: } \lim_{x \to -\infty} \text{softplus}(x) = 0, \quad \lim_{x \to \infty} \text{softplus}(x) = x\]
Praktische Berechnungsbeispiele
📝 Beispiel 1: Grundlegende Berechnungen
Aufgabe: Softplus-Werte für verschiedene Eingaben
Berechnung:
\[\text{softplus}(-2) = \ln(1 + e^{-2}) = \ln(1 + 0{,}135) \approx 0{,}127\] \[\text{softplus}(-1) = \ln(1 + e^{-1}) = \ln(1 + 0{,}368) \approx 0{,}313\] \[\text{softplus}(0) = \ln(1 + e^0) = \ln(2) \approx 0{,}693\] \[\text{softplus}(1) = \ln(1 + e^1) = \ln(1 + 2{,}718) \approx 1{,}313\] \[\text{softplus}(2) = \ln(1 + e^2) = \ln(1 + 7{,}389) \approx 2{,}127\]
Beobachtung: Für x > 2 nähert sich softplus(x) ≈ x an
📝 Beispiel 2: Vergleich mit ReLU
Aufgabe: Unterschiede zwischen Softplus und ReLU
Eingabe: x = 0.5
Berechnung:
\[\text{ReLU}(0{,}5) = \max(0, 0{,}5) = 0{,}5\] \[\text{Softplus}(0{,}5) = \ln(1 + e^{0{,}5}) = \ln(1 + 1{,}649) \approx 0{,}974\] \[\text{Differenz: } \text{softplus}(0{,}5) - \text{ReLU}(0{,}5) \approx 0{,}474\] \[\text{Bei } x = -0{,}5: \text{ReLU}(-0{,}5) = 0, \quad \text{softplus}(-0{,}5) \approx 0{,}474\]
Vorteil: Softplus ist auch für negative Eingaben differenzierbar
📝 Beispiel 3: Variational Autoencoder
Aufgabe: Softplus als Aktivierung für Varianz-Parameter
Kontext: VAE Encoder-Netzwerk
Anwendung:
\[\text{Encoder Output: } \mu, \log\sigma^2 = \text{Neural Network}(x)\] \[\text{Varianz-Aktivierung: } \sigma^2 = \text{softplus}(\log\sigma^2)\] \[\text{Warum Softplus: } \sigma^2 > 0 \text{ (Varianz muss positiv sein)}\] \[\text{Reparameterization: } z = \mu + \sigma \cdot \epsilon, \quad \epsilon \sim \mathcal{N}(0,1)\]
Vorteil: Garantiert positive Varianz ohne harte Beschränkungen
Vor- und Nachteile
✅ Vorteile der Softplus-Funktion
Positive Eigenschaften im Vergleich zu anderen Aktivierungsfunktionen:
\[\text{✓ Überall differenzierbar (auch bei x=0)}\] \[\text{✓ Immer positive Ausgabe: softplus(x) > 0}\] \[\text{✓ Glatte Approximation von ReLU}\] \[\text{✓ Keine Dead Neurons wie bei ReLU}\] \[\text{✓ Konvexe Funktion}\] \[\text{✓ Numerisch stabile Berechnung}\]
⚠️ Nachteile und Limitationen
Herausforderungen bei der Verwendung:
\[\text{⚠ Rechenaufwändiger als ReLU (Exponentialfunktion)}\] \[\text{⚠ Kann zu Vanishing Gradients führen für sehr negative x}\] \[\text{⚠ Nicht so weit verbreitet wie ReLU}\] \[\text{⚠ Baseline-Offset von ln(2) bei x=0}\] \[\text{⚠ Potentiell langsameres Training}\]
Vergleichstabelle der Aktivierungsfunktionen
📊 Funktionswerte-Vergleich
| Input x | Softplus | ReLU | Leaky ReLU | ELU |
|---|---|---|---|---|
| -3 | 0.049 | 0 | -0.03 | -0.950 |
| -1 | 0.313 | 0 | -0.01 | -0.632 |
| 0 | 0.693 | 0 | 0 | 0 |
| 1 | 1.313 | 1 | 1 | 1 |
| 3 | 3.049 | 3 | 3 | 3 |
| 5 | 5.007 | 5 | 5 | 5 |
Anwendungen in verschiedenen Bereichen
🧠 Neuronale Netze
- • Alternative zu ReLU in Hidden Layers
- • Glatte Gradientenflüsse
- • Vermeidung von Dead Neurons
- • Bessere Konvergenz-Eigenschaften
📊 Probabilistische Modelle
- • Variational Autoencoders (VAEs)
- • Positive Parameter-Aktivierung
- • Bayesianische Neuronale Netze
- • Gaußsche Prozess-Approximationen
🔬 Forschung
- • Kontinuierliche Optimierung
- • Gradientenfluss-Analysen
- • Aktivierungsfunktions-Studien
- • Theoretische Untersuchungen
⚙️ Spezialanwendungen
- • Kontinuierliche Kontrolle
- • Robotik und Reinforcement Learning
- • Physik-informierte Neuronale Netze
- • Signal-Verarbeitung
Implementierung und Code
💻 Code-Implementierungen
Implementierung der Softplus-Funktion:
Python (NumPy):
def softplus(x):
return np.log(1 + np.exp(x))
# Numerisch stabile Version
def stable_softplus(x):
return np.maximum(x, 0) + np.log1p(np.exp(-np.abs(x)))
def softplus_derivative(x):
return 1 / (1 + np.exp(-x)) # = sigmoid(x)
TensorFlow/Keras:
tf.nn.softplus(x)
# oder als Layer:
tf.keras.activations.softplus
PyTorch:
torch.nn.functional.softplus(x)
# oder als Layer:
torch.nn.Softplus()
🎯 Praktische Anwendung
Verwendung in neuronalen Netzen:
Keras/TensorFlow Beispiel:
model = tf.keras.Sequential([
tf.keras.layers.Dense(64, activation='softplus'),
tf.keras.layers.Dense(32, activation='softplus'),
tf.keras.layers.Dense(10, activation='softmax')
])
# VAE Encoder mit Softplus für Varianz
class VAEEncoder(tf.keras.layers.Layer):
def call(self, inputs):
h = tf.keras.layers.Dense(64, activation='relu')(inputs)
mu = tf.keras.layers.Dense(latent_dim)(h)
log_var = tf.keras.layers.Dense(latent_dim)(h)
sigma = tf.nn.softplus(log_var) # Positive Varianz
return mu, sigma
PyTorch Beispiel:
class Net(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 128)
self.fc2 = nn.Linear(128, 64)
self.fc3 = nn.Linear(64, 10)
self.softplus = nn.Softplus()
def forward(self, x):
x = self.softplus(self.fc1(x))
x = self.softplus(self.fc2(x))
return self.fc3(x)
🎯 Numerische Stabilität
Optimierte Implementation für große Werte:
Problem: exp(x) kann overflow für große x
Lösung: Numerisch stabile Version
def stable_softplus(x):
"""
Numerisch stabile Softplus-Implementation
Verwendet log1p und abs für Stabilität
"""
# Für x > 0: softplus(x) ≈ x + log1p(exp(-x))
# Für x < 0: softplus(x) = log1p(exp(x))
return np.where(x > 0,
x + np.log1p(np.exp(-x)),
np.log1p(np.exp(x)))
# Alternative: TensorFlow-Style
def tf_style_softplus(x, threshold=20):
return np.where(x > threshold, x, np.log1p(np.exp(x)))
💡 Wichtige Eigenschaften der Softplus-Funktion:
- Glättung: softplus(x) = ln(1+e^x) - überall differenzierbar
- Positivität: Immer positive Ausgabe, ideal für Varianz-Parameter
- ReLU-Approximation: Für große x verhält sich wie ReLU
- Kontinuität: Keine sprunghaften Änderungen oder tote Neuronen
🔬 Anwendungsgebiete der Softplus-Funktion:
- Neuronale Netze: Glatte Alternative zu ReLU-Aktivierung
- VAEs: Positive Parameter-Aktivierung für Varianz
- Probabilistische Modelle: Kontinuierliche positive Ausgaben
- Kontinuierliche Optimierung: Differenzierbare Relaxation
acos - Arkuskosinus
acot - Arkuskotangens
acsc - Arkuskosekans
asec - Arkussekans
asin - Arkussinus
atan - Arkustangens
atan2 - Arkustangens von y/x
cos - Kosinus
cot - Kotangens
csc - Kosekans
sec - Sekans
sin - Sinus
sinc - Kardinalsinus
tan - Tangens
hypot - Hypotenuse
deg2rad - Grad in Radiant
rad2deg - Radiant in Grad
Hyperbolik
acosh - Arkuskosinus hyperbolikus
asinh - Areasinus hyperbolikus
atanh - Arkustangens hyperbolikus
cosh - Kosinus hyperbolikus
sinh - Sinus hyperbolikus
tanh - Tangens hyperbolikus
Logarithmus
log - Logarithmus zur angegebene Basis
ln - Natürlicher Logarithmus zur Basis e
log10 - Logarithmus zur Basis 10
log2 - Logarithmus zur Basis 2
exp - Exponenten zur Basis e
Aktivierung
Softmax
Sigmoid
Derivate Sigmoid
Logit
Derivate Logit
Softsign
Derivate Softsign
Softplus
Logistic
Gamma
Eulersche Gamma Funktion
Lanczos Gamma-Funktion
Stirling Gamma-Funktion
Log Gamma-Funktion
Beta
Beta Funktion
Logarithmische Beta Funktion
Unvollstaendige Beta Funktion
Inverse unvollstaendige Beta Funktion
Fehlerfunktionen
erf - Fehlerfunktion
erfc - komplementäre Fehlerfunktion
Kombinatorik
Fakultät
Semifakultät
Steigende Fakultät
Fallende Fakultät
Subfakultät
Permutationen und Kombinationen
Permutation
Kombinationen
Mittlerer Binomialkoeffizient
Catalan-Zahl
Lah Zahl