Arkussekans (asec) Rechner
Berechnung des Winkels zum gegebenen Sekanswert mit mathematischen Eigenschaften
Geben Sie den Sekanswert ein (|x| ≥ 1) und klicken Sie auf Berechnen um den entsprechenden Winkel zu ermitteln. Der Arkussekans ist die Umkehrfunktion von sec.
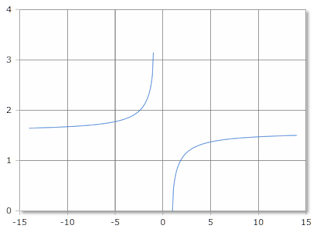
Graphische Darstellung der asec-Funktion
Arkussekans (Inverser Sekans)
Arkussekans verstehen
Der Arkussekans (asec) ist die Umkehrfunktion des Sekans. Er berechnet den Winkel α, für den sec(α) = x gilt. Diese Funktion ist nur für |x| ≥ 1 definiert und hat einen Wertebereich von [0, π] \ {π/2}.
📐 Definition
Umkehrfunktion von sec:
📊 Eigenschaften
- • Definitionsbereich: \((-\infty, -1] \cup [1, \infty)\)
- • Wertebereich: \([0, \pi] \setminus \{\frac{\pi}{2}\}\)
- • Wertebereich: \([0°, 180°] \setminus \{90°\}\)
- • Gerade Funktion
🔬 Anwendungen
- • Geometrie und Trigonometrie
- • Physik (Optik, Mechanik)
- • Ingenieurswesen
- • Astronomie
⭐ Spezielle Werte
- • \(\text{asec}(1) = 0° = 0\)
- • \(\text{asec}(-1) = 180° = \pi\)
- • \(\text{asec}(2) = 60° = \frac{\pi}{3}\)
- • \(\text{asec}(\sqrt{2}) = 45° = \frac{\pi}{4}\)
Mathematische Eigenschaften
📐 Grundbeziehung
Definition des Arkussekans:
\[y = \text{asec}(x) \Leftrightarrow \sec(y) = x\] \[\text{für } |x| \geq 1 \text{ und } y \in [0, \pi] \setminus \left\{\frac{\pi}{2}\right\}\]
Beziehung zu arccos: \(\text{asec}(x) = \arccos\left(\frac{1}{x}\right)\) für \(|x| \geq 1\)
🔄 Wichtige Beziehungen
Zusammenhänge mit anderen Funktionen:
\[\text{asec}(x) = \arccos\left(\frac{1}{x}\right) \text{ für } |x| \geq 1\] \[\text{asec}(-x) = \pi - \text{asec}(x) \text{ für } x \geq 1\] \[\sec(\text{asec}(x)) = x \text{ für alle } |x| \geq 1\] \[\text{asec}(x) + \text{acsc}(x) = \frac{\pi}{2} \text{ für } x \geq 1\]
📊 Ableitung und Integration
Differential- und Integralrechnung:
\[\frac{d}{dx}\text{asec}(x) = \frac{1}{|x|\sqrt{x^2-1}} \text{ für } |x| > 1\] \[\int \text{asec}(x) \, dx = x \cdot \text{asec}(x) - \ln\left|x + \sqrt{x^2-1}\right| + C\] \[\int \frac{1}{|x|\sqrt{x^2-1}} \, dx = \text{asec}(x) + C\]
Beachte: Die Ableitung ist immer positiv für x > 1 und negativ für x < -1
Praktische Berechnungsbeispiele
📝 Beispiel 1: Rechtwinkliges Dreieck
Aufgabe: Winkel aus Seitenverhältnissen berechnen
Gegeben: Hypotenuse \(c = 10\), Ankathete \(b = 5\)
Berechnung:
\[\sec(\alpha) = \frac{\text{Hypotenuse}}{\text{Ankathete}} = \frac{10}{5} = 2\] \[\alpha = \text{asec}(2) = \arccos\left(\frac{1}{2}\right) = 60°\] \[\text{In Radiant: } \alpha = \frac{\pi}{3} \approx 1{,}047 \text{ rad}\]
Verifikation: \(\sec(60°) = \frac{1}{\cos(60°)} = \frac{1}{0{,}5} = 2\) ✓
📝 Beispiel 2: Spezielle Winkel
Aufgabe: Bekannte Sekanswerte und ihre Winkel
Berechnung:
\[\text{asec}(1) = \arccos(1) = 0° = 0 \text{ rad}\] \[\text{asec}(\sqrt{2}) = \arccos\left(\frac{1}{\sqrt{2}}\right) = 45° = \frac{\pi}{4} \text{ rad}\] \[\text{asec}(2) = \arccos\left(\frac{1}{2}\right) = 60° = \frac{\pi}{3} \text{ rad}\] \[\text{asec}(-1) = \arccos(-1) = 180° = \pi \text{ rad}\]
Merkhilfe: asec(x) = arccos(1/x) für die häufigsten Werte
📝 Beispiel 3: Optische Brechung
Aufgabe: Brechungswinkel bei Totalreflexion
Gegeben: Brechungsindex \(n = 1{,}5\)
Berechnung:
\[\text{Grenzwinkel: } \sin(\theta_c) = \frac{1}{n} = \frac{1}{1{,}5} = \frac{2}{3}\] \[\text{Dann: } \cos(\theta_c) = \sqrt{1 - \sin^2(\theta_c)} = \sqrt{1 - \frac{4}{9}} = \frac{\sqrt{5}}{3}\] \[\sec(\theta_c) = \frac{1}{\cos(\theta_c)} = \frac{3}{\sqrt{5}} = \frac{3\sqrt{5}}{5} \approx 1{,}34\] \[\theta_c = \text{asec}(1{,}34) \approx 41{,}8°\]
Anwendung: Glasfasertechnik, Optik, Photonik
Geometrische Interpretation
🔵 Sekans und rechtwinkliges Dreieck
Geometrische Bedeutung im rechtwinkligen Dreieck:
\[\sec(\alpha) = \frac{\text{Hypotenuse}}{\text{Ankathete}} = \frac{c}{b}\] \[\text{Dann: } \alpha = \text{asec}\left(\frac{c}{b}\right)\] \[\text{Bedingung: } \frac{c}{b} \geq 1 \text{ (immer erfüllt, da } c \geq b \text{)}\] \[\text{Pythagoras: } c^2 = a^2 + b^2\]
Interpretation: asec gibt den Winkel für ein gegebenes Hypotenuse-zu-Ankathete-Verhältnis an
💡 Wichtige Eigenschaften der asec-Funktion:
- Definitionsbereich: \((-\infty, -1] \cup [1, \infty)\) (außerhalb (-1, 1))
- Wertebereich: \([0, \pi] \setminus \{\frac{\pi}{2}\}\) bzw. \([0°, 180°] \setminus \{90°\}\)
- Symmetrie: Nicht symmetrisch, aber \(\text{asec}(-x) = \pi - \text{asec}(x)\)
- Beziehung: \(\text{asec}(x) = \arccos\left(\frac{1}{x}\right)\)
🔬 Anwendungsgebiete der asec-Funktion:
- Geometrie: Winkelberechnung bei gegebenen Seitenverhältnissen
- Physik: Optik (Brechung, Reflexion) und Mechanik
- Ingenieurswesen: Strukturanalyse und trigonometrische Berechnungen
- Astronomie: Koordinatentransformationen und Winkelberechnungen
acos - Arkuskosinus
acot - Arkuskotangens
acsc - Arkuskosekans
asec - Arkussekans
asin - Arkussinus
atan - Arkustangens
atan2 - Arkustangens von y/x
cos - Kosinus
cot - Kotangens
csc - Kosekans
sec - Sekans
sin - Sinus
sinc - Kardinalsinus
tan - Tangens
hypot - Hypotenuse
deg2rad - Grad in Radiant
rad2deg - Radiant in Grad
Hyperbolik
acosh - Arkuskosinus hyperbolikus
asinh - Areasinus hyperbolikus
atanh - Arkustangens hyperbolikus
cosh - Kosinus hyperbolikus
sinh - Sinus hyperbolikus
tanh - Tangens hyperbolikus
Logarithmus
log - Logarithmus zur angegebene Basis
ln - Natürlicher Logarithmus zur Basis e
log10 - Logarithmus zur Basis 10
log2 - Logarithmus zur Basis 2
exp - Exponenten zur Basis e
Aktivierung
Softmax
Sigmoid
Derivate Sigmoid
Logit
Derivate Logit
Softsign
Derivate Softsign
Softplus
Logistic
Gamma
Eulersche Gamma Funktion
Lanczos Gamma-Funktion
Stirling Gamma-Funktion
Log Gamma-Funktion
Beta
Beta Funktion
Logarithmische Beta Funktion
Unvollstaendige Beta Funktion
Inverse unvollstaendige Beta Funktion
Fehlerfunktionen
erf - Fehlerfunktion
erfc - komplementäre Fehlerfunktion
Kombinatorik
Fakultät
Semifakultät
Steigende Fakultät
Fallende Fakultät
Subfakultät
Permutationen und Kombinationen
Permutation
Kombinationen
Mittlerer Binomialkoeffizient
Catalan-Zahl
Lah Zahl