Einweggleichrichter mit Kondensator Rechner
Berechnung von Brummspannung, Ladespannung und Glättung bei Kondensator-Siebung
Geben Sie die Eingangsspannung, Kondensatorwerte und Lastparameter ein und klicken Sie auf Berechnen um die Ausgangsspannungen und Brummspannung des Einweggleichrichters mit Kondensator-Glättung zu ermitteln.
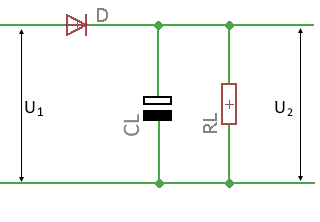
Einweggleichrichter mit Kondensator verstehen
Der Einweggleichrichter mit Ladekondensator ist eine Erweiterung der einfachen Halbwellengleichrichtung. Der Kondensator lädt sich während der positiven Halbwelle auf und entlädt sich über die Last während der negativen Halbwelle. Dies führt zu einer deutlich geglätteten Ausgangsspannung, die jedoch noch eine Brummspannung aufweist.
🔋 Funktionsprinzip
Lade-/Entladezyklus:
🌊 Brummspannung
Welligkeit der DC-Spannung:
✅ Vorteile
- • Deutlich geglättete Ausgangsspannung
- • Höhere Ausgangsspannung
- • Einfacher Aufbau
- • Kostengünstige Lösung
❌ Nachteile
- • Hohe Spitzenströme durch Diode
- • Doppelte Sperrspannung (2×√2×Ueff)
- • Schlechte Regelung bei Laständerung
- • Immer noch erhebliche Brummspannung
Grundformeln der Kondensator-Glättung
🔋 Leerlaufspannung
Maximale Spannung ohne Last:
\[U_{Leer} = \sqrt{2} \cdot U_{1eff} - U_{Diode}\] \[U_{Leer} = U_S - U_D\]
ULeer: Kondensator lädt sich auf Spitzenspannung minus Diodenspannung
⚡ Spannung unter Last
Ausgangsspannung bei Belastung:
\[U_{Last} = U_{Leer} \left( 1 - \sqrt{\frac{R_i}{R_L}} \right)\] \[\text{Vereinfacht: } U_{Last} \approx U_{Leer} \text{ (wenn } R_i \ll R_L \text{)}\]
Ri: Innenwiderstand der Quelle (Trafowicklung + Leitungen)
🌊 Brummspannung (Ripple)
Wechselspannungsanteil der Ausgangsspannung:
\[U_{BrSS} = \frac{U_{Last}}{C \cdot R_L \cdot f} \left( 1 - \sqrt[4]{\frac{R_i}{R_L}} \right)\] \[\text{Vereinfacht: } U_{BrSS} \approx \frac{U_{Last}}{C \cdot R_L \cdot f}\] \[U_{max} = U_{Last} + \frac{U_{BrSS}}{2}\] \[U_{min} = U_{Last} - \frac{U_{BrSS}}{2}\]
⚠️ Sperrspannung
Maximale Rückwärtsspannung an der Diode:
\[U_{Sperr} = 2\sqrt{2} \cdot U_{1eff}\] \[\text{Bei } U_{eff} = 230V: U_{Sperr} = 651V\]
Wichtig: Doppelte Spitzenspannung! Diode muss entsprechend dimensioniert werden.
Signalverläufe und Betrieb
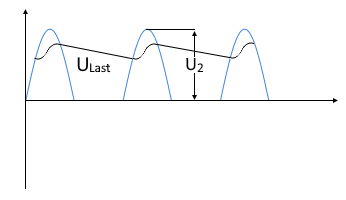
Spannungsverlauf mit Kondensator
Geglättete Gleichspannung mit Brummspannungsanteil
Praktische Beispiele
📝 Beispiel 1: 12V-Netzteil
Aufgabe: 12V-Netzteil mit Kondensator-Glättung
Gegeben: Ueff = 15V, C = 2200μF, RL = 120Ω, Ri = 2Ω, f = 50Hz
Berechnung:
\[U_{Leer} = 15 \cdot \sqrt{2} - 0,7 = 20,5 \text{ V}\] \[U_{Last} = 20,5 \cdot \left(1 - \sqrt{\frac{2}{120}}\right) = 17,6 \text{ V}\] \[U_{BrSS} = \frac{17,6}{2200 \times 10^{-6} \cdot 120 \cdot 50} = 1,33 \text{ V}\] \[U_{min} = 17,6 - 0,67 = 16,9 \text{ V}\]
Ergebnis: 12V-Netzteil mit 1,33V Brummspannung (11% Ripple).
📝 Beispiel 2: Spannungsvervielfacher
Aufgabe: Hochspannungsversorgung mit kleinem Kondensator
Gegeben: Ueff = 230V, C = 10μF, RL = 10kΩ, Ri = 50Ω, f = 50Hz
Berechnung:
\[U_{Leer} = 230 \cdot \sqrt{2} - 0,7 = 324,6 \text{ V}\] \[U_{BrSS} = \frac{324,6}{10 \times 10^{-6} \cdot 10000 \cdot 50} = 64,9 \text{ V}\] \[U_{Sperr} = 2 \cdot 230 \cdot \sqrt{2} = 651 \text{ V}\]
Ergebnis: Hohe Brummspannung (20%), Diode muss 651V Sperrspannung aushalten.
Praktische Anwendungen
💡 Einfache Netzteile
- • Einfache DC-Versorgungen
- • LED-Treiber mit Glättung
- • Batterieladegeräte
- • Kleine Verbraucher-Elektronik
⚡ Hochspannungsanwendungen
- • Spannungsvervielfacher
- • CRT-Anodenvorsorgung
- • Röhrenverstärker-Anodenvorsorgung
- • HV-Laborversorgungen
⚠️ Wichtige Sicherheitshinweise:
- Hohe Sperrspannung: Diode muss 2×√2×Ueff aushalten (bei 230V: 651V!)
- Spitzenströme: Sehr hohe Einschaltströme beim Laden des Kondensators
- Kondensator-Entladung: Kondensator bleibt nach Abschalten geladen!
- Strombegrenzung: Vorwiderstand oder Drossel zur Strombegrenzung nötig
💡 Praktische Tipps:
- Kondensator-Größe: C ≥ 1000μF pro Ampere Laststrom für gute Glättung
- Spannungsfestigkeit: Kondensator muss mindestens 1,5×ULeer aushalten
- Entladeweg: Parallelwiderstand (≈10×RL) für sichere Entladung
- Dioden-Schutz: Soft-Start oder Strombegrenzung gegen Einschaltstrom
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode