Pi-Dämpfungsglied Rechner
Rechner und Formeln zur Berechnung der Widerstände eines Pi-Dämpfungsglied
Hinweis zur Bedienung: Wählen Sie die Berechnungsmethode (dB-Dämpfung oder Spannungsverhältnis), geben Sie die Systemimpedanz und die entsprechenden Werte ein. Der Rechner berechnet die beiden Widerstandswerte R₁ (Serie) und R₂ (Parallel) für das π-Dämpfungsglied.
Standard-Impedanzen:
- 50Ω: Standard in der Hochfrequenztechnik (Funk, Mobilfunk)
- 75Ω: Standard in der Videotechnik (Antenne, Kabel-TV)
- 600Ω: Standard in der professionellen Audiotechnik
- 100Ω: Differenzielle Signale (Ethernet, USB)
Grundbegriffe einfach erklärt
π-Dämpfungsglied: "Kontrollierte Signalabschwächung mit Impedanzanpassung"
Ein π-Dämpfungsglied reduziert die Signalamplitude um einen definierten Betrag, während es
gleichzeitig die Impedanz des Systems konstant hält.
Serienwiderstand R₁: "Verbindung zwischen Ein- und Ausgang"
Dieser Widerstand liegt im Signalweg und bestimmt hauptsächlich die Dämpfung.
Parallelwiderstände R₂: "Impedanzanpassung am Ein- und Ausgang"
Diese identischen Widerstände sorgen für die korrekte Impedanz und Reflexionsfreiheit.
Praktische Anwendungsbeispiele
Beispiel 1 - HF-Messtechnik:
"50Ω-System, 20dB Dämpfung für Oszilloskop-Messung:"
R₁ = 50Ω × (10² - 1) ÷ (2 × 10) = 247.5Ω
R₂ = 50Ω × (10 + 1) ÷ (10 - 1) = 61.1Ω
Beispiel 2 - Audio-Dämpfung:
"600Ω-Audio-System, 6dB Dämpfung (Faktor 2):"
R₁ = 600Ω × (2² - 1) ÷ (2 × 2) = 450Ω
R₂ = 600Ω × (2 + 1) ÷ (2 - 1) = 1800Ω
Beispiel 3 - Video-Technik:
"75Ω-Video-System, 10dB Dämpfung:"
a = 10^(10/20) = 3.16
R₁ = 75Ω × (3.16² - 1) ÷ (2 × 3.16) = 186Ω
R₂ = 75Ω × (3.16 + 1) ÷ (3.16 - 1) = 144Ω
Dämpfungsglied-Topologien im Vergleich
| Topologie | Aufbau | Vorteile | Nachteile |
|---|---|---|---|
| π-Glied | 2 Parallel-, 1 Serienwiderstand | Gute Impedanzanpassung | Höhere Verlustleistung |
| T-Glied | 2 Serien-, 1 Parallelwiderstand | Geringere Verluste | Schlechteres Reflexionsverhalten |
| L-Glied | 1 Serien-, 1 Parallelwiderstand | Einfachster Aufbau | Begrenzte Dämpfungswerte |
Anwendungsgebiete
Hochfrequenztechnik:
- Signalgeneratoren: Ausgangspegelanpassung
- Verstärker: Zwischen Stufen zur Entkopplung
- Messgeräte: Eingangsschutz und Pegelanpassung
- Antennentechnik: SWR-Verbesserung
Audiotechnik:
- Mischpulte: Kanalanpassung
- Verstärker: Pegeldämpfung
- Messgeräte: Eingangsdämpfung
- Studioequipment: Signalrouting
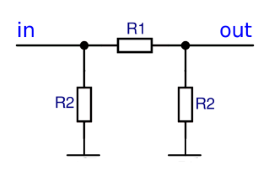
Schaltbild eines π-Dämpfungsglieds
Formeln zum π-Dämpfungsglied
Grundformeln
Dämpfungsfaktor aus dB-Wert: \[\displaystyle a = \frac{U_1}{U_2} = 10^{\frac{\Delta L_{dB}}{20}}\]
Dämpfungsfaktor aus Spannungsverhältnis: \[\displaystyle a = \frac{U_{ein}}{U_{aus}}\]
Widerstandsberechnung
Serienwiderstand R₁: \[\displaystyle R_1 = Z \times \frac{a^2 - 1}{2a}\]
Parallelwiderstände R₂: \[\displaystyle R_2 = Z \times \frac{a + 1}{a - 1}\]
Legende:
- \(a\) - Dämpfungsfaktor (linear)
- \(\Delta L_{dB}\) - Dämpfung in Dezibel
- \(Z\) - Systemimpedanz (Ω)
- \(R_1\) - Serienwiderstand (Ω)
- \(R_2\) - Parallelwiderstand (Ω)
- \(U_1, U_{ein}\) - Eingangsspannung
- \(U_2, U_{aus}\) - Ausgangsspannung
Rechenbeispiel 1: Standard HF-Dämpfungsglied
50Ω-System, 6dB Dämpfung: \[a = 10^{6/20} = 1.995 \approx 2\] \[R_1 = 50\Omega \times \frac{2^2 - 1}{2 \times 2} = 50\Omega \times \frac{3}{4} = 37.5\Omega\] \[R_2 = 50\Omega \times \frac{2 + 1}{2 - 1} = 50\Omega \times 3 = 150\Omega\]
Rechenbeispiel 2: Hohe Dämpfung
75Ω-Video-System, 40dB Dämpfung: \[a = 10^{40/20} = 100\] \[R_1 = 75\Omega \times \frac{100^2 - 1}{2 \times 100} = 75\Omega \times \frac{9999}{200} = 3749.6\Omega\] \[R_2 = 75\Omega \times \frac{100 + 1}{100 - 1} = 75\Omega \times \frac{101}{99} = 76.5\Omega\]
Erweiterte Berechnungen
Verlustleistung im Dämpfungsglied: \[\displaystyle P_{verlust} = P_{ein} \times \left(1 - \frac{1}{a^2}\right)\]
Rückflussdämpfung (Return Loss):
Bei korrekter Dimensionierung ist die Rückflussdämpfung theoretisch unendlich groß.
Bandbreite:
Reine Widerstandsnetzwerke sind frequenzunabhängig und haben theoretisch unbegrenzte Bandbreite.
Praktische Dimensionierung
Widerstandstoleranz:
- Standard-Anwendungen: 5% Toleranz ausreichend
- Messgeräte: 1% oder besser erforderlich
- Hochpräzision: 0.1% für Labor-Standards
Leistungsberechnung:
Die maximale Eingangsleistung ist durch den schwächsten Widerstand begrenzt:
\[\displaystyle P_{max} = \min\left(\frac{U_{max}^2}{R_1}, \frac{U_{max}^2}{R_2}\right)\]
Frequenzverhalten
Ideales Verhalten:
Reine Widerstandsnetzwerke sind frequenzunabhängig und haben konstante Dämpfung
von DC bis in den GHz-Bereich.
Parasitäre Effekte:
- Induktivität: Drahtwiderstände bei hohen Frequenzen
- Kapazität: Gehäuse und Leiterbahnen
- Skin-Effekt: Frequenzabhängiger Widerstand
Aufbau-Varianten
Diskrete Widerstände:
- THT-Widerstände: Für Prototypen und Reparaturen
- SMD-Widerstände: Kompakte Bauweise
- Precision-Widerstände: Für Messgeräte
Integrierte Lösungen:
- Dünnfilm-Netzwerke: Höchste Präzision
- Keramik-Substrate: HF-optimiert
- Koaxiale Dämpfungsglieder: 50Ω-Standard
Qualitätskriterien
Wichtige Parameter:
- Dämpfungsgenauigkeit: ±0.1dB für Präzisionsanwendungen
- Rückflussdämpfung: >30dB für gute Anpassung
- Frequenzgang: ±0.1dB über den Nutzbereich
- Temperaturstabilität: <50ppm /°C
Fehlervermeidung
Häufige Fehler:
- Falsche Impedanz: Berücksichtigung der Systemimpedanz
- Überlastung: Leistungsberechnung beachten
- Parasitäre Effekte: Layout bei hohen Frequenzen
- Toleranzen: Widerstandsstreuung in der Serienfertigung
Das π-Dämpfungsglied ist eine fundamentale Schaltung in der Signal- und Hochfrequenztechnik. Seine Fähigkeit zur kontrollierten Signaldämpfung bei gleichzeitiger Impedanzanpassung macht es unverzichtbar für Messgeräte, Signalgeneratoren und HF-Systeme. Die korrekte Dimensionierung ist entscheidend für optimale Systemperformance.
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode