Widerstand Parallelschaltung für 2 Widerstände Rechner
Rechner und Formel zur Berechnung zweier Widerstände einer Parallelschaltung
Hinweis zur Bedienung: Wählen Sie, was berechnet werden soll (Gesamtwiderstand oder Parallelwiderstand R₂). Geben Sie die bekannten Widerstandswerte ein. Der Rechner berechnet den gesuchten Wert nach den Gesetzen der Parallelschaltung.
Wichtige Eigenschaften der Parallelschaltung:
- Spannung: An allen Widerständen gleich (U₁ = U₂ = Uges)
- Strom: Teilt sich auf (Iges = I₁ + I₂)
- Gesamtwiderstand: Immer kleiner als der kleinste Einzelwiderstand
- Anwendung: Haushaltsgeräte, LED-Beleuchtung, Messtechnik
Grundbegriffe einfach erklärt
Parallelschaltung: "Mehrere Wege für den Strom"
Bei einer Parallelschaltung sind die Widerstände nebeneinander geschaltet. Der Strom kann
sich auf verschiedene Wege aufteilen, wie Wasser in mehreren parallel verlaufenden Rohren.
Gesamtwiderstand: "Der Widerstand, den die ganze Schaltung bietet"
Da der Strom mehrere Wege hat, ist der Gesamtwiderstand immer kleiner als jeder Einzelwiderstand.
Mehr parallele Wege = weniger Gesamtwiderstand.
Stromaufteilung: "Umgekehrt proportional zum Widerstand"
Der Strom fließt bevorzugt durch den kleineren Widerstand. Bei gleichen Widerständen
teilt sich der Strom gleichmäßig auf.
Praktische Anwendungsbeispiele
Beispiel 1 - LED-Parallelschaltung:
"Zwei LEDs mit je 330Ω Vorwiderstand parallel geschaltet:"
Rges = (330Ω × 330Ω) ÷ (330Ω + 330Ω) = 165Ω
→ Gesamtstrom verdoppelt sich, jede LED bekommt halben Strom
Beispiel 2 - Messbereichserweiterung:
"Amperemeter 1mA Vollausschlag, Ri=100Ω, gewünschter Bereich 10mA:"
Rshunt = (100Ω × (1mA÷9mA)) ÷ (100Ω - (1mA÷9mA)) = 11,11Ω
→ 9mA fließen durch Shunt, 1mA durch Messwerk
Beispiel 3 - Hausinstallation:
"Steckdosenkreis: mehrere Verbraucher parallel an 230V:"
Jeder Verbraucher bekommt volle Spannung, Ströme addieren sich am Sicherungsautomaten.
Parallelschaltung vs. Reihenschaltung
| Eigenschaft | Parallelschaltung | Reihenschaltung |
|---|---|---|
| Spannung | An jedem Widerstand gleich | Teilt sich auf die Widerstände auf |
| Strom | Teilt sich auf die Widerstände auf | Durch jeden Widerstand gleich |
| Gesamtwiderstand | Kleiner als kleinster Einzelwiderstand | Summe aller Einzelwiderstände |
| Ausfallsicherheit | Ein Widerstand defekt → andere funktionieren | Ein Widerstand defekt → Kreis unterbrochen |
| Anwendung | Hausinstallation, Beleuchtung | Spannungsteiler, Messschaltungen |
Anwendungsgebiete der Parallelschaltung
Haushalts- und Gebäudetechnik:
- Steckdosenkreise: Jede Steckdose hat volle Netzspannung
- Beleuchtung: Schalter für einzelne Lampen möglich
- Haushaltsgeräte: Unabhängiger Betrieb verschiedener Geräte
Elektronik und Messtechnik:
- Messbereichserweiterung: Shunt-Widerstände für Amperemeter
- Stromteiler: Definierte Stromaufteilung
- Redundanz: Backup-Pfade für kritische Schaltungen
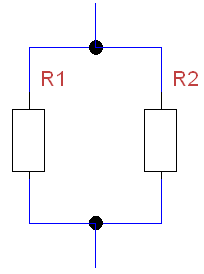
Schaltbild einer Parallelschaltung zweier Widerstände
Formeln zur Parallelschaltung
Grundformeln
Leitwert-Addition (allgemeine Form): \[\displaystyle \frac{1}{R_{ges}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + ...\]
Für zwei Widerstände (Produktformel): \[\displaystyle R_{ges} = \frac{R_1 \times R_2}{R_1 + R_2}\]
Umstellungen und Ableitungen
Parallelwiderstand R₂ berechnen: \[\displaystyle R_2 = \frac{R_1 \times R_{ges}}{R_1 - R_{ges}}\]
R₁ berechnen (falls R₂ und Rges bekannt): \[\displaystyle R_1 = \frac{R_2 \times R_{ges}}{R_2 - R_{ges}}\]
Legende:
- \(R_{ges}\) - Gesamtwiderstand der Parallelschaltung (Ω)
- \(R_1, R_2\) - Einzelwiderstände (Ω)
- \(I_{ges}\) - Gesamtstrom (A)
- \(I_1, I_2\) - Teilströme durch die Widerstände (A)
- \(U\) - Spannung (an allen Widerständen gleich) (V)
Rechenbeispiel 1: Standard-Parallelschaltung
Zwei Widerstände 60Ω und 30Ω parallel: \[R_{ges} = \frac{60\Omega \times 30\Omega}{60\Omega + 30\Omega} = \frac{1800}{90} = 20\Omega\] Kontrolle über Leitwerte: \[\frac{1}{R_{ges}} = \frac{1}{60\Omega} + \frac{1}{30\Omega} = 0,0167 + 0,0333 = 0,05\text{S}\] \[R_{ges} = \frac{1}{0,05\text{S}} = 20\Omega\] ✓
Rechenbeispiel 2: Gesuchter Parallelwiderstand
R₁ = 100Ω, gewünschter Rges = 40Ω. Welcher R₂? \[R_2 = \frac{100\Omega \times 40\Omega}{100\Omega - 40\Omega} = \frac{4000}{60} = 66,67\Omega\] Verifikation: \[R_{ges} = \frac{100\Omega \times 66,67\Omega}{100\Omega + 66,67\Omega} = 40\Omega\] ✓
Erweiterte Berechnungen
Stromaufteilung bei Parallelschaltung: \[\displaystyle I_1 = I_{ges} \times \frac{R_2}{R_1 + R_2}\] \[\displaystyle I_2 = I_{ges} \times \frac{R_1}{R_1 + R_2}\]
Leistungsverteilung: \[\displaystyle P_1 = \frac{U^2}{R_1}, \quad P_2 = \frac{U^2}{R_2}\] \[\displaystyle P_{ges} = P_1 + P_2 = U^2 \times \left(\frac{1}{R_1} + \frac{1}{R_2}\right)\]
Besondere Fälle
Gleiche Widerstände parallel:
Bei n gleichen Widerständen R parallel:
\[\displaystyle R_{ges} = \frac{R}{n}\]
Beispiel: 3 × 90Ω parallel → Rges = 30Ω
Sehr unterschiedliche Widerstände:
Wenn R₁ << R₂, dann Rges ≈ R₁
Der kleinere Widerstand dominiert das Ergebnis.
Praktische Dimensionierung
Shunt-Widerstand für Messbereichserweiterung: \[\displaystyle R_{shunt} = \frac{R_{Messwerk}}{n-1}\] wobei n = gewünschter Erweiterungsfaktor
Stromteiler-Verhältnis:
Für Verhältnis I₁:I₂ = 1:k:
\[\displaystyle R_2 = \frac{R_1}{k}\]
Toleranzbetrachtungen
Auswirkung von Widerstandstoleranzen:
Bei Widerständen mit ±5% Toleranz kann Rges um ±3% bis ±7% schwanken,
abhängig von den Widerstandswerten und deren Korrelation.
Fehlerquellen und -vermeidung
Häufige Rechenfehler:
- Reihenschaltungs-Formel verwendet: Rges = R₁ + R₂ (falsch!)
- Division vergessen: Rges = R₁ × R₂ ohne ÷(R₁ + R₂)
- Einheiten nicht beachtet: Mischung von Ω, kΩ, MΩ
Messtechnische Anwendungen
Innenwiderstand von Messgeräten:
Voltmeter parallel: Rges = RSchaltung || RVoltmeter
→ Hochohmiges Voltmeter erforderlich (RV >> RSchaltung)
Die Parallelschaltung ist fundamental für die Elektrotechnik und ermöglicht den unabhängigen Betrieb verschiedener Verbraucher bei konstanter Spannung. Das Verständnis der Strom- und Widerstandsgesetze ist essentiell für sichere und effiziente Schaltungsdesigns in Haushalt, Industrie und Elektronik.
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode