R/C zur Ladespannung Rechner
Berechnung von R oder C zu einer gegebenen Ladespannung zu einem Zeitpunkt
R/C Dimensionierung für RC-Glieder
Mit diesem Rechner können Sie den Widerstand R oder die Kapazität C eines RC-Glieds berechnen, um eine bestimmte Ladespannung zu einem gewünschten Zeitpunkt zu erreichen. Dies ist besonders nützlich für die Dimensionierung von Timer-Schaltungen, Verzögerungsgliedern und RC-Filtern.
🔧 Widerstand R
- • Bestimmt Ladegeschwindigkeit
- • Begrenzt den Ladestrom
- • R = τ / C
⚡ Kapazität C
- • Speichert elektrische Energie
- • Bestimmt Zeitkonstante
- • C = τ / R
⏱️ Zeitkonstante τ
- • τ = R × C
- • Nach 1τ: 63,2% geladen
- • Nach 5τ: 99,3% geladen
Berechnungsformeln
🔋 Grundformel der Ladespannung
Die Ladespannung eines Kondensators folgt der Exponentialfunktion:
\[ U_C(t) = U \cdot \left(1 - e^{-\frac{t}{\tau}}\right) \]
Wobei: UC(t) = Ladespannung zur Zeit t, U = Eingangsspannung, τ = R × C
🔧 Widerstand R berechnen
Der erforderliche Widerstand für eine gewünschte Ladespannung:
\[ R = \frac{t \cdot (-1)}{C \cdot \ln\left(1-\frac{U_L}{U}\right)} \]
Wobei: UL = gewünschte Ladespannung, t = Zeit, C = Kapazität
⚡ Kapazität C berechnen
Die erforderliche Kapazität für eine gewünschte Ladespannung:
\[ C = \frac{t \cdot (-1)}{R \cdot \ln\left(1-\frac{U_L}{U}\right)} \]
Wobei: UL = gewünschte Ladespannung, t = Zeit, R = Widerstand
Praktische Beispiele
📝 Beispiel 1: Timer-Schaltung
Aufgabe: Ein 555-Timer soll nach 1 Sekunde auslösen (63,2% von 5V = 3,16V)
Gegeben: C = 1000 μF, U = 5V, UL = 3,16V, t = 1s
Gesucht: R = ?
\[ R = \frac{1 \cdot (-1)}{1000 \times 10^{-6} \cdot \ln(1-\frac{3{,}16}{5})} = \frac{-1}{0{,}001 \cdot \ln(0{,}368)} = 1000 \text{ Ω} \]
Ergebnis: Ein 1 kΩ Widerstand erzeugt die gewünschte Verzögerung von 1 Sekunde.
📝 Beispiel 2: Blinkschaltung
Aufgabe: Kondensator soll sich in 500ms auf 90% der Spannung laden
Gegeben: R = 10 kΩ, U = 12V, UL = 10,8V, t = 0,5s
Gesucht: C = ?
\[ C = \frac{0{,}5 \cdot (-1)}{10000 \cdot \ln(1-\frac{10{,}8}{12})} = \frac{-0{,}5}{10000 \cdot \ln(0{,}1)} = 21{,}7 \text{ μF} \]
Ergebnis: Ein 22 μF Kondensator (nächster Normwert) ist erforderlich.
Schaltbild und Anwendungen
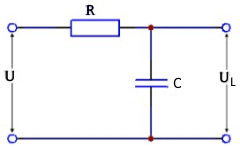
⏰ Timer-Anwendungen
- • 555-Timer Schaltungen
- • Verzögerungsrelais
- • Blinkschaltungen
- • Einschaltverzögerungen
🎛️ Filter-Anwendungen
- • Tiefpass-Filter
- • Anti-Aliasing Filter
- • Störspannungsunterdrückung
- • Glättungsschaltungen
💡 Praktische Tipps:
- Toleranzen: Verwenden Sie Bauteile mit niedrigen Toleranzen für präzise Zeiten
- Temperatur: Kondensatoren sind oft temperaturabhängig (besonders Elkos)
- Leckstrom: Bei langen Zeiten (>1min) niedrige Leckströme beachten
- Normwerte: Wählen Sie den nächsten verfügbaren Normwert für R oder C
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode