Belasteter Spannungsteiler Rechner
Onlinerechner zur Berechnung der Werte an einem belasteten Spannungsteiler
Hinweis zur Bedienung: Geben Sie die Gesamtspannung sowie R₁ und R₂ ein. Wählen Sie dann entweder die gewünschte Ausgangsspannung U₂ oder den bekannten Lastwiderstand RL. Der Rechner berechnet alle anderen Werte automatisch.
Wichtige Eigenschaften des belasteten Spannungsteilers:
- Lasteinfluss: RL parallel zu R₂ reduziert den effektiven Widerstand
- Spannungsabsenkung: Die Ausgangsspannung sinkt unter Last
- Stromaufteilung: Der Strom teilt sich zwischen R₂ und RL auf
- Anwendung: Realistische Spannungsteiler mit angeschlossenen Lasten
Grundbegriffe einfach erklärt
Belasteter Spannungsteiler: "Spannungsteiler mit angeschlossener Last"
Im Gegensatz zum unbelasteten Spannungsteiler ist hier eine Last (RL) parallel zu R₂ geschaltet.
Dies verändert das Teilerverhältnis und reduziert die Ausgangsspannung.
Parallelwiderstand R₂||RL: "Effektiver unterer Widerstand"
R₂ und RL bilden zusammen einen Parallelwiderstand, der kleiner ist als jeder Einzelwiderstand.
Dieser bestimmt das neue Teilerverhältnis.
Stromaufteilung: "Strom verteilt sich auf R₂ und RL"
Der Strom I₁ fließt durch R₁, teilt sich dann aber auf R₂ und RL auf.
Die Aufteilung erfolgt umgekehrt proportional zu den Widerstandswerten.
Praktische Anwendungsbeispiele
Beispiel 1 - ADC-Eingangsbeschaltung mit Schutzwiderstand:
"5V Signal für 3.3V ADC, R₁=10kΩ, R₂=20kΩ, ADC-Eingangswiderstand 1MΩ:"
R₂L = (20kΩ × 1MΩ)/(20kΩ + 1MΩ) = 19.6kΩ
U₂ = 5V × 19.6kΩ/(10kΩ + 19.6kΩ) = 3.31V ≈ 3.3V ✓
Beispiel 2 - Versorgungsspannung für LED-Treiber:
"12V auf 9V für LED-Modul mit 300Ω Eingangswiderstand:"
Gewünscht: U₂ = 9V bei Uein = 12V, RL = 300Ω
Mit R₂ = 1kΩ → R₂L = (1kΩ × 300Ω)/(1kΩ + 300Ω) = 231Ω
R₁ = 231Ω × (12V-9V)/9V = 77Ω
Beispiel 3 - Bias-Spannungsteiler mit Op-Amp-Last:
"Symmetrische ±15V Versorgung, Mittenanzapfung 0V, Op-Amp-Eingangsstrom 1µA:"
Bei hochohmigen Lasten (MΩ-Bereich) ist der Lasteinfluss vernachlässigbar.
R₁ = R₂ = 10kΩ → U₂ = 15V (praktisch unbelastet)
Lasteffekt-Tabelle
| Lastverhältnis RL/R₂ | R₂L/R₂ | Spannungsreduktion | Praktische Bedeutung |
|---|---|---|---|
| ∞ (unbelastet) | 1,00 | 0% | Idealer Spannungsteiler |
| 10:1 | 0,91 | 8% | Geringer Lasteinfluss |
| 5:1 | 0,83 | 15% | Merklicher Einfluss |
| 2:1 | 0,67 | 25% | Starker Lasteinfluss |
| 1:1 | 0,50 | 33% | Halbierung der Spannung |
| 1:2 | 0,33 | 50% | Sehr starker Einfluss |
Anwendungsgebiete belasteter Spannungsteiler
Praktische Schaltungen:
- ADC-Eingänge: Messbereichsanpassung mit endlichem Eingangswiderstand
- Bias-Netzwerke: Arbeitspunkteinstellung von Transistoren
- Referenzspannungen: Mit definierten Lasten (z.B. Op-Amp-Eingänge)
- Sensor-Interfaces: Signalkonditionierung mit nachfolgender Elektronik
Designüberlegungen:
- Lastanalyse: Eingangswiderstand der nachfolgenden Schaltung bestimmen
- Querstrom-Dimensionierung: Mindestens 10× größer als Laststrom
- Toleranzbetrachtung: Lasteinfluss bei Worst-Case-Bedingungen
- Pufferung: Op-Amp-Follower für hochohmige Lasten

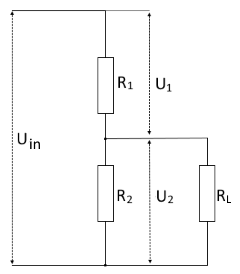
Schaltbild eines belasteten Spannungsteilers mit Lastwiderstand RL
Formeln zum belasteten Spannungsteiler
Grundformeln
Parallelwiderstand R₂||RL: \[\displaystyle R_{2L} = \frac{R_2 \times R_L}{R_2 + R_L}\]
Ausgangsspannung mit Last: \[\displaystyle U_2 = U_{ein} \times \frac{R_{2L}}{R_1 + R_{2L}}\]
Gesamtwiderstand: \[\displaystyle R_{ges} = R_1 + R_{2L}\]
Stromberechnungen
Strom durch R₁ (Gesamtstrom): \[\displaystyle I_1 = \frac{U_{ein}}{R_{ges}} = \frac{U_1}{R_1}\]
Strom durch R₂: \[\displaystyle I_2 = \frac{U_2}{R_2}\]
Strom durch RL (Laststrom): \[\displaystyle I_L = \frac{U_2}{R_L}\]
Umkehrformeln
RL bei gegebener Ausgangsspannung: \[\displaystyle R_L = \frac{R_2 \times R_{2L}}{R_2 - R_{2L}}\] wobei \(R_{2L} = \frac{U_2 \times R_1}{U_{ein} - U_2}\)
Benötigte Spannung U₂ bei gegebenem RL: \[\displaystyle U_2 = U_{ein} \times \frac{R_2 \times R_L}{R_1(R_2 + R_L) + R_2 \times R_L}\]
Legende:
- \(U_{ein}\) - Eingangsspannung (V)
- \(U_1, U_2\) - Teilspannungen (V)
- \(R_1\) - Oberer Widerstand (Ω)
- \(R_2\) - Unterer Widerstand (Ω)
- \(R_L\) - Lastwiderstand (Ω)
- \(R_{2L}\) - Parallelwiderstand R₂||RL (Ω)
- \(I_1, I_2, I_L\) - Teilströme (A)
Rechenbeispiel 1: ADC-Eingangsbeschaltung
Gegeben: Uein = 5V, R₁ = 10kΩ, R₂ = 20kΩ, RL = 1MΩ (ADC-Eingangswiderstand) Parallelwiderstand: \[R_{2L} = \frac{20k\Omega \times 1M\Omega}{20k\Omega + 1M\Omega} = \frac{20 \times 10^9}{1.02 \times 10^6} = 19.61k\Omega\] Ausgangsspannung: \[U_2 = 5V \times \frac{19.61k\Omega}{10k\Omega + 19.61k\Omega} = 5V \times 0.662 = 3.31V\] Ohne Last wäre: U₂ = 5V × 20kΩ/30kΩ = 3.33V
Spannungsreduktion: (3.33V - 3.31V)/3.33V = 0.6% (vernachlässigbar)
Rechenbeispiel 2: Niederohimige Last
Gegeben: Uein = 12V, R₁ = R₂ = 1kΩ, gewünschte U₂ = 5V Ohne Last: U₂ = 6V
Benötigter R2L für 5V: R2L = 5V × 1kΩ/(12V-5V) = 714Ω Benötigter Lastwiderstand: \[R_L = \frac{1k\Omega \times 714\Omega}{1k\Omega - 714\Omega} = \frac{714k}{286} = 2.5k\Omega\] Ströme: I₁ = 12V/(1kΩ + 714Ω) = 7mA
I₂ = 5V/1kΩ = 5mA, IL = 5V/2.5kΩ = 2mA
Kontrolle: I₁ = I₂ + IL = 5mA + 2mA = 7mA ✓
Praktische Designregeln
Minimierung des Lasteffekts:
- Regel: RL >> R₂ (mindestens 10× größer)
- Pufferung: Op-Amp-Follower für niederohmige Lasten
- Querstrom-Design: ITeiler >> ILast
Worst-Case-Analyse:
- Minimale Last: Höchste Ausgangsspannung
- Maximale Last: Niedrigste Ausgangsspannung
- Toleranzen: Widerstandstoleranzen beeinflussen das Ergebnis
Temperatur- und Toleranzeffekte
Temperatureinfluss:
Bei unterschiedlichen Temperaturkoeffizienten von R₂ und RL ändert sich das Teilerverhältnis:
\[\Delta U_2 = U_2 \times \frac{\Delta R_{2L}}{R_1 + R_{2L}}\]
Toleranz-Fortpflanzung:
Die Ausgangsspannung ist besonders empfindlich gegenüber Änderungen von RL bei niederohmigen Lasten.
Frequenzverhalten
Kapazitive Lasten:
Bei kapazitiven Lasten (z.B. ADC-Sample&Hold) entstehen Tiefpass-Charakteristiken:
\[f_{-3dB} = \frac{1}{2\pi \times R_{aus} \times C_L}\]
wobei Raus = R₁||R₂ die Ausgangsimpedanz ist.
Leistungsbetrachtungen
Verlustleistungen: \[P_1 = I_1^2 \times R_1, \quad P_2 = I_2^2 \times R_2, \quad P_L = I_L^2 \times R_L\] \[P_{ges} = P_1 + P_2 + P_L = U_{ein} \times I_1\]
Wirkungsgrad: \[\eta = \frac{P_L}{P_{ges}} = \frac{U_2 \times I_L}{U_{ein} \times I_1}\]
Der belastete Spannungsteiler ist die realistische Betrachtung von Spannungsteilern, da in praktischen Anwendungen immer eine Last angeschlossen ist. Das Verständnis des Lasteffekts und der daraus resultierenden Spannungsreduzierung ist essentiell für das Design zuverlässiger Analog-Schaltungen. Die richtige Dimensionierung unter Berücksichtigung der Last gewährleistet die gewünschte Funktionalität auch unter realen Betriebsbedingungen.
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode