RC-Grenzfrequenz Rechner
Berechnung von RC-Grenzfrequenz: Widerstand, Kapazität und -3dB-Punkt für Filter und Signalverarbeitung
Zur Berechnung wählen Sie zunächst mit den Button aus, was Sie berechnen möchten. Danach geben Sie die beiden fehlenden Werte ein. Anschließend klicken Sie auf den Button Beechnen .
RC-Grenzfrequenz verstehen
Die RC-Grenzfrequenz ist ein fundamentaler Parameter in der Elektrotechnik und Signalverarbeitung. Sie markiert den -3dB-Punkt, bei dem die Ausgangsspannung auf etwa 70,7% (1/√2) der Eingangsspannung abfällt. An diesem Punkt sind Wirk- und Blindwiderstand gleich groß: R = XC.
📊 Grenzfrequenz fg
Die fundamentale Beziehung:
⚡ Impedanz-Gleichheit
An der Grenzfrequenz gilt:
⏰ Zeitkonstante τ
Verbindung zur Grenzfrequenz:
🌊 Kreisfrequenz ωg
Alternative Darstellung:
Grundformeln der RC-Grenzfrequenz
📊 Grundlegende Beziehungen
Die fundamentalen Formeln für RC-Grenzfrequenzen:
\[f_g = \frac{1}{2\pi RC}\] \[R = \frac{1}{2\pi f_g C}\] \[C = \frac{1}{2\pi f_g R}\]
Zusätzlich: ωg = 2πfg = 1/(RC), τ = RC = 1/(2πfg)
🔧 Übertragungsverhalten
Das Frequenzverhalten von RC-Gliedern:
\[H(jω) = \frac{1}{1 + jωRC}\] \[|H(jω)| = \frac{1}{\sqrt{1 + (ωRC)^2}}\] \[φ(ω) = -\arctan(ωRC)\]
Bei ω = ωg: \(|H| = \frac{1}{\sqrt{2}} ≈ 0,707 (-3dB), \qquad φ = -45°\)
Praktische Beispiele
📝 Beispiel 1: Audio-Tiefpass für Subwoofer
Aufgabe: Tiefpass mit fg = 120 Hz für Subwoofer-Abtrennung
Gegeben: fg = 120 Hz, gewünschter Widerstand R = 8 Ω
Berechnung:
\[C = \frac{1}{2\pi f_g R} = \frac{1}{2\pi \cdot 120 \cdot 8} = 166 \text{ μF}\]
Ergebnis: C = 166 μF, praktisch 150 μF verwenden.
📝 Beispiel 2: AC-Kopplung für Vorverstärker
Aufgabe: Hochpass für AC-Kopplung, fg = 20 Hz
Gegeben: C = 10 μF vorhanden, gesucht: R = ?
Berechnung:
\[R = \frac{1}{2\pi f_g C} = \frac{1}{2\pi \cdot 20 \cdot 10 \times 10^{-6}} = 796 \text{ Ω}\]
Ergebnis: R = 796 Ω, praktisch 820 Ω (E12-Reihe) verwenden.
Frequenzgang und Anwendungen
📈 Frequenzgang-Charakteristik
- • f << fg: Nahezu keine Dämpfung
- • f = fg: -3dB Dämpfung, -45° Phase
- • f >> fg: -20dB/Dekade Abfall
- • DC-Verhalten: Kondensator = Unterbrechung
🎛️ Filtertypen
- • RC-Tiefpass: R vor C (zum Ausgang)
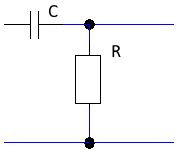
- • RC-Hochpass: C vor R (zum Ausgang)
- • Gleiche fg: Beide verwenden fg = 1/(2πRC)
- • Komplementär: Hochpass + Tiefpass
Praktische Anwendungen
🎵 Audio-Technik
- • Lautsprecher-Frequenzweichen
- • Subsonic- und Ultraschallfilter
- • Entzerrung und Klangregelung
- • Anti-Aliasing-Filter
📡 Signalverarbeitung
- • AC/DC-Kopplung zwischen Stufen
- • EMV- und Störfilter
- • Bandbreitenbegrenzung
- • Oszilloskop-Eingangsteiler
💡 Praktische Tipps:
- Bauteilwahl: Verwenden Sie Standardwerte (E12/E24-Reihen) für R und C
- Toleranzen: ±20% Toleranz führt zu ±20% Abweichung bei fg
- Temperatur: Kondensatoren sind meist temperaturstabiler als Widerstände
- Impedanz: Quellenimpedanz << R << Lastimpedanz für optimale Funktion
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode