Zweiweg-Gleichrichter mit Kondensator Rechner
Berechnung von Brummspannung, Ladespannung und optimaler Glättung bei Vollwellengleichrichtung
Geben Sie die Eingangsspannung, Kondensatorwerte und Lastparameter ein und klicken Sie auf Berechnen um die Ausgangsspannungen und Brummspannung des Brückengleichrichters mit optimaler Kondensator-Glättung zu ermitteln.
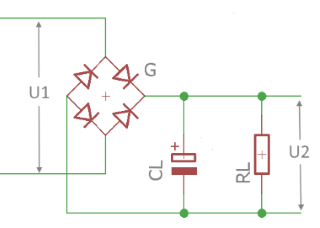
Zweiweg-Gleichrichter mit Kondensator verstehen
Der Brückengleichrichter mit Ladekondensator ist die optimale Kombination aus Vollwellengleichrichtung und Kondensator-Glättung. Die vier Dioden nutzen beide Halbwellen und der Kondensator speichert Energie zwischen den Spitzen. Dies führt zu minimaler Brummspannung bei 100Hz Ripple-Frequenz (doppelte Netzfrequenz).
🌉 Optimales Prinzip
Vollwellengleichrichtung + Glättung:
🌊 Reduzierte Brummspannung
Optimierte Welligkeit:
✅ Überlegene Vorteile
- • Minimale Brummspannung (halbe Einweg)
- • Doppelte Ripple-Frequenz (100Hz)
- • Hohe Ausgangsspannung
- • Optimale Transformator-Ausnutzung
❌ Geringe Nachteile
- • Vier Dioden erforderlich
- • Höhere Kosten als Einweg
- • Sperrspannung = √2×Ueff (niedriger!)
- • Spitzenströme beim Einschalten
Formeln der optimierten Brückengleichrichtung
🔋 Leerlaufspannung (Brücke vs. Mittelpunkt)
Spannungsabfälle und Ausgangsleistung:
\[\text{Brückengleichrichter: } U_{Leer} = \sqrt{2} \cdot U_{1eff} - 2 \times U_D\] \[\text{Mittelpunkt-Gleichrichter: } U_{Leer} = \sqrt{2} \cdot U_{1eff} - U_D\] \[\text{Standardwerte: } 2 \times U_D = 1,4V \text{ (Brücke)}, U_D = 0,7V \text{ (Mittelpunkt)}\]
Vorteil Mittelpunkt: Weniger Spannungsabfall, aber Trafo mit Mittelanzapfung nötig
⚡ Spannung unter Last
Belastungseinfluss mit Innenwiderstand:
\[U_{Last} = U_{Leer} \left( 1 - \sqrt{\frac{R_i}{2 \times R_L}} \right)\] \[\text{Vereinfacht: } U_{Last} \approx U_{Leer} \text{ (wenn } R_i \ll R_L \text{)}\] \[I_{Last} = \frac{U_{Last}}{R_L}\]
Faktor 2: Bessere Lastregulierung als bei Einweggleichrichter
🌊 Optimierte Brummspannung
Halbierte Welligkeit durch Vollwellengleichrichtung:
\[U_{BrSS} = \frac{U_{Last}}{2 \times C \times R_L \times f} \left( 1 - \sqrt[4]{\frac{R_i}{2 \times R_L}} \right)\] \[\text{Vereinfacht: } U_{BrSS} \approx \frac{U_{Last}}{2 \times C \times R_L \times f}\] \[\text{Ripple-Frequenz: } f_{ripple} = 2 \times f_{netz} = 100Hz\] \[U_{max} = U_{Last} + \frac{U_{BrSS}}{2}, \quad U_{min} = U_{Last} - \frac{U_{BrSS}}{2}\]
⚠️ Geringere Sperrspannung
Vorteil gegenüber Einweggleichrichter:
\[U_{Sperr} = \sqrt{2} \times U_{1eff}\] \[\text{Vergleich Einweg: } U_{Sperr,Einweg} = 2\sqrt{2} \times U_{1eff}\] \[\text{Bei } U_{eff} = 230V: U_{Sperr,Brücke} = 325V \text{ vs. } 651V\]
Vorteil: Nur halbe Sperrspannung im Vergleich zu Einweggleichrichtern!
Signalverläufe und Betrieb
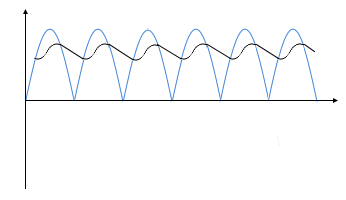
Eingangsspannung US
Sinusförmige Wechselspannung für Vollwellengleichrichtung
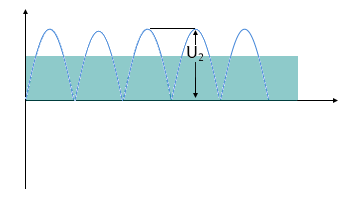
Ausgangsspannung U₂
Vollwellen mit Kondensator-Glättung, 100Hz Ripple
Praktische Beispiele
📝 Beispiel 1: 24V-Labornetzteil
Aufgabe: Hochwertiges 24V-Netzteil mit minimaler Brummspannung
Gegeben: Ueff = 18V, C = 4700μF, RL = 24Ω (1A), Ri = 1Ω, f = 50Hz
Berechnung:
\[U_{Leer} = 18 \cdot \sqrt{2} - 1,4 = 24,0 \text{ V}\] \[U_{Last} = 24,0 \cdot \left(1 - \sqrt{\frac{1}{2 \times 24}}\right) = 22,5 \text{ V}\] \[U_{BrSS} = \frac{22,5}{2 \times 4700 \times 10^{-6} \times 24 \times 50} = 0,20 \text{ V}\] \[\text{Ripple: } \frac{0,20}{22,5} = 0,9\% \text{ (excellent!)}\]
Ergebnis: Hochqualitatives 24V-Netzteil mit nur 0,9% Brummspannung!
📝 Beispiel 2: PC-Netzteil Vorstufe
Aufgabe: 300V-Zwischenkreis für Schaltnetzteil
Gegeben: Ueff = 230V, C = 220μF, RL = 1000Ω, Ri = 5Ω, f = 50Hz
Berechnung:
\[U_{Leer} = 230 \cdot \sqrt{2} - 1,4 = 324,1 \text{ V}\] \[U_{Last} = 324,1 \cdot \left(1 - \sqrt{\frac{5}{2 \times 1000}}\right) = 322,6 \text{ V}\] \[U_{BrSS} = \frac{322,6}{2 \times 220 \times 10^{-6} \times 1000 \times 50} = 14,7 \text{ V}\] \[U_{Sperr} = 230 \cdot \sqrt{2} = 325 \text{ V (machbar!)}\]
Ergebnis: 322V DC mit 4,6% Ripple, ideal für nachfolgende Schaltregler.
Vergleich: Brücke vs. Mittelpunkt-Gleichrichter
🌉 Brückengleichrichter
- • Dioden: 4 Stück
- • Spannungsabfall: 2×UD = 1,4V
- • Trafo: Einfache Sekundärwicklung
- • Standard: Universell einsetzbar
⚡ Mittelpunkt-Gleichrichter
- • Dioden: 2 Stück
- • Spannungsabfall: 1×UD = 0,7V
- • Trafo: Mittelpunkt-Anzapfung nötig
- • Spezial: Für niedrige Spannungen
Praktische Anwendungen
🖥️ PC und IT-Technik
- • PC-Netzteil Eingangsstufe
- • Server-Stromversorgungen
- • Notebook-Adapter
- • USV-Anlagen
🔬 Labor und Industrie
- • Regelbare Labornetzteile
- • Präzisions-DC-Quellen
- • Konstantstrom-Versorgungen
- • Mess- und Prüfgeräte
🎵 Audio und HiFi
- • HiFi-Verstärker
- • Studio-Equipment
- • PA-Anlagen
- • Röhrenverstärker
⚡ Hochleistungsanwendungen
- • Schweißgeräte
- • Elektrolyse-Anlagen
- • Motor-Antriebe
- • Induktionsheizung
💡 Praktische Dimensionierungsregeln:
- Kondensator-Größe: C ≥ 1000μF pro Ampere für <5% Ripple
- Spannungsfestigkeit: Kondensator mindestens 1,5×ULeer
- Dioden-Strom: IF ≥ 3×ILast (Spitzenströme beim Einschalten)
- Sperrspannung: Dioden mindestens 2×ULeer (Sicherheitsfaktor)
🏆 Warum Brückengleichrichter mit Kondensator optimal sind:
- Minimale Brummspannung: Halbiert gegenüber Einweggleichrichter
- Hohe Ripple-Frequenz: 100Hz leichter zu filtern als 50Hz
- Geringere Sperrspannung: Sicherere Dioden-Dimensionierung
- Universell einsetzbar: Von mW bis kW-Bereich bewährt
Mittelpunkt-Gleichrichter Alternative
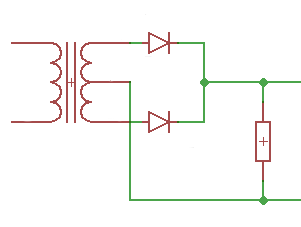
Mittelpunkt-Gleichrichter
Alternative mit nur 2 Dioden, aber Trafo-Mittelpunkt erforderlich
🔄 Mittelpunkt-Gleichrichter Formel
Für Niederspannungs-Anwendungen mit weniger Diodenverlusten:
\[U_{Leer} = \sqrt{2} \times U_{1eff} - U_{Diode}\] \[\text{Nur eine Diode im Strompfad: } U_{Diode} = 0,7V\] \[\text{Vorteil: } 0,7V \text{ weniger Verlust als Brücke}\] \[\text{Nachteil: } \text{Trafo mit Mittelpunkt-Anzapfung nötig}\]
Einsatz: Bevorzugt bei niedrigen Spannungen (3V, 5V, 12V) wo Diodenverlusten kritisch sind
Grundlagen
Leitungswiderstand
kVA aus Ampere und Volt
Dezibel in linearen Faktor umrechnen
Dezibel, Spannung, Leistung umrechnen
Ohmsche Gesetz
Coulombsche Gesetz
Batterie Kapazität
Elektrizitätsmenge
Elektrische Energie
Elektrische Leistung
Elektrische Ladung
Innenwiderstand einer Stromquelle
Kondensator Kapazität
Spannungverlust auf einer Leitung
Tabelle der Temperaturkoeffizienten
Temperaturabhängigkeit vom Widerstand
Schaltungen mit Widerständen
PI-Dämpfungsglied
T-Dämpfungsglied
2 Parallelwiderstände
Mehrere Parallelwiderstände
Serienwiderstände
unbelasteter Spannungsteiler
belasteter Spannungsteiler
Vorwiderstand (Voltmeter)
Parallelwiderstand (Ampermeter)
Schaltungen mit Kondensatoren
Mehrere Kondensatoren Reihenschaltung
Zwei Kondensatoren Reihenschaltung
Blindwiderstand XC eines Kondensators
Zeitkonstante eines R/C-Glieds
Ladespannung zu einem Zeitpunkt
Kondensatorspannung zu einem Zeitpunkt
R oder C zu einer Ladespannung
RC Reihenschaltung
RC Parallelschaltung
RC Hochpass
RC Tiefpass
RC Differenzierer
RC Integrierierer
RC Grenzfrequenz berechnen
R + C bei gegebener Impedanz
Schaltungen mit Spulen
Induktivität einer Spule
Blindwiderstand einer Spule
L/R Reihenschaltung
L/R Parallelschaltung
L/R Hochpass
L/R Tiefpass
L/R Grenzfrequenz
L/R Differenzierglied
Transformator
Kondensatoren und Spulen
Resonanzfrequenz
Serienschwingkreis
Parallelschwingkreis
Parallelschaltung
Serienschaltung
Gleichrichter- und Dioden
Einweg Gleichrichtung
Einweg Gleichrichtung mit Ladekondensator
Zweiweg Gleichrichtung
Zweiweg Gleichrichtung mit Ladekondensator
LED Vorwiderstand
Vorwiderstand zur Zenerdiode mit variabler Last
Vorwiderstand zur Zenerdiode